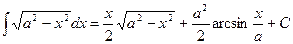|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие неопределенного интегралаСтр 1 из 12Следующая ⇒
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ КОЛЛЕДЖ СВЯЗИ Федерального государственного образовательного бюджетного учреждения Высшего профессионального образования «Поволжский государственный университет телекоммуникаций и информатики» УТВЕРЖДАЮ: Зам. директора по УПР _______Черненкова Н.В. «____»__________2012г. СБОРНИК Практических занятий
По дисциплине: «Элементы высшей математики» Номера работ: № 17 – 30 для специальностей: 230115 – «Программирование в компьютерных системах» 230401 – «Информационные системы»
Каждая работа рассчитана на 2 часа
Составлен преподавателем Лобачевой М.Е. Рассмотрен на заседании П(Ц)К «Естественнонаучные и общепрофессиональные дисциплины» Протокол № 5 от 11.01.2012г. Председатель П(Ц)К________Лобачева М.Е.
Самара, 2012 г Практическое занятие №17 Наименование занятия: Интегрирование заменой переменной и по частям В неопределенном интеграле Цель занятия:Научиться вычислять неопределенные интегралы методами введения новой переменной, по частям. Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной». Литература: Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г. Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Понятие неопределенного интеграла
Функция F(x) называется первообразной от функции f(x) на отрезке [a;b], если во всех точках этого отрезка выполняется равенство: F′(x) = f(x). Если функция F(x) является первообразной для функции f(x), то выражение F(x) + C называется неопределенным интегралом от функции f(x) и обозначается: ∫ f(x)dx. Свойства неопределенного интеграла: 1) Производная от неопределенного интеграла равна подынтегральной функции, т.е. (ò f(x)dx)′ = f(x) 2) Постоянный множитель можно выносить за знак интеграла, т.е. ò a∙f(x)dx=a∙ò f(x)dx (a=const) 3) Интеграл от суммы (или разности) двух функций равен сумме (или разности) интегралов от этих функций, т.е. ò (f(x) ±g(x))dx = ò f(x)dx ± ò g(x)dx.
Таблица основных интегралов
1. 2. 3. 4. 5. 6. 7. 8. ∫ tg x dx = - 9. ∫ ctg x dx = 10. 11. 12. 13. 14. 15. 16. 17. 18. Методы интегрирования
Поиск по сайту: |

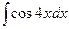
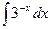
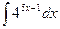
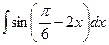


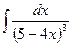
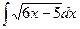
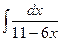

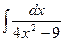
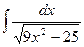

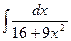
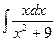
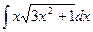

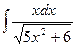
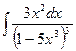
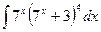

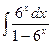
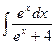
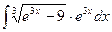

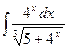
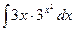
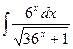
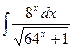
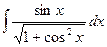


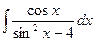
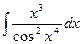
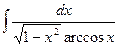
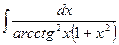



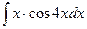
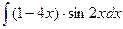

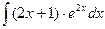

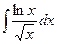
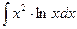
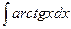
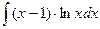
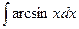

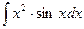
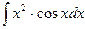

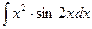

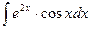
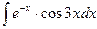
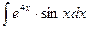
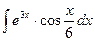
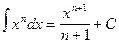 , (n ≠ -1)
, (n ≠ -1)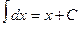
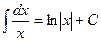

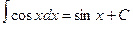
 tg x + C
tg x + C -ctg x+ C
-ctg x+ C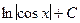
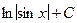
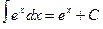
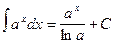
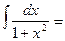 arctg x +C
arctg x +C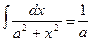 arctg
arctg 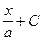

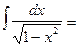 arcsin x + C
arcsin x + C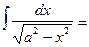 arcsin
arcsin 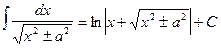
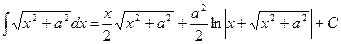 19.
19.