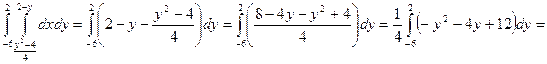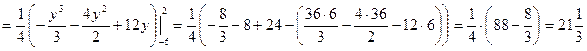|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Случай прямоугольной области
Двойной интеграл по прямоугольной области
Пример 1. Вычислить двойной интеграл Решение. В соответствии с формулой (1) запишем Таким образом,
Случай криволинейной области Если функция f(x, y) непрерывна в замкнутой области G, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и j £ y, тогда
Если функция f(x, y) непрерывна в замкнутой области G, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то
Пример 2. Вычислить интеграл Решение. Построим область G и вычислим интеграл по формуле (3)
G
0 2 x
Пример 3. Вычислить интеграл y = x, x = 0, y = 1, y = 2. Решение. Построим область G и вычислим интеграл по формуле (4)
y
y = x G
0 x
Практическое занятие №25 Наименование занятия: Приложения двойных интегралов Цель занятия:Научиться применять двойные интегралы к вычислению площадей фигур. Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции нескольких действительных переменных». Литература:
Задание на занятие:
Используя двойной интеграл, вычислить площади фигур, ограниченных линиями:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Геометрические приложения двойных интегралов Вычисление площадей в декартовых координатах
y = j(x) S y = f(x) a b x
Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:
Пример 1. Вычислить площадь фигуры, ограниченной линиями y2 = 4x + 4; x + y – 2 = 0.
Линии пересекаются в двух точках – (0, 2) и (8, -6). Таким образом, область интегрирования ограничена по оси Ох графиками кривых от S =
Поиск по сайту: |
 вычисляется по формулам:
вычисляется по формулам: (1)
(1)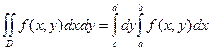 (2)
(2)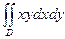 , где
, где 
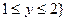
 . Вычислим внутренний интеграл, считая переменную х постоянным числом:
. Вычислим внутренний интеграл, считая переменную х постоянным числом: 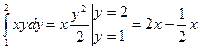 . Затем вычисляем внешний интеграл по переменной х:
. Затем вычисляем внешний интеграл по переменной х:  .
.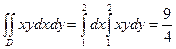
 (3)
(3) (4)
(4)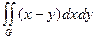 , если область G ограничена линиями: y = 0, y = x2, x = 2.
, если область G ограничена линиями: y = 0, y = x2, x = 2. y
y =
= 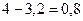
 , если область G ограничена линиями
, если область G ограничена линиями

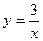 ,
,
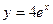 ,
у = 3,
у = 4
,
у = 3,
у = 4
 ,
,
 ,
у = 2,
у = 5
,
у = 2,
у = 5
 ,
у = 2,
у = 7
,
у = 2,
у = 7
 ,
,
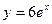 ,
у = 1,
у = 6
,
у = 1,
у = 6
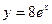 ,
у = 3,
у = 8
,
у = 3,
у = 8
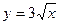 ,
,
 ,
, 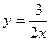 ,
х = 4
,
х = 4
 ,
,
 ,
, 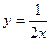 ,
х = 16
,
х = 16
 ,
, 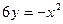

 ,
, 
 х = 0
х = 0
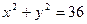 ,
, 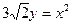

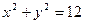 ,
, 


 y
y

 до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна:
до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна: