 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегрирование по частям в определенном интеграле
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
Выбор u и dv осуществляется также как и в неопределенном интеграле. Пример 3. Решение. Выполним замену. Положим
Практическое занятие №21 Наименование занятия: Решение прикладных задач с помощью Определенного интеграла Цель занятия:Научиться вычислять определенные интегралы, находить площади фигур, ограниченных линиями. Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной». Литература:
Задание на занятие: ВАРИАНТ 1 1. Вычислить работу, совершенную при сжатии пружины на 8 см, если для сжатия ее на 1 см нужно приложить силу в 10 Н.
2. Скорость движения точки меняется по закону v = 4t – t2, где v – скорость, м/с; t – время, с. Вычислить: путь, пройденный точкой за третью секунду движения; путь, пройденный точкой за промежуток времени [0; 6].
3. Найти площадь фигуры, ограниченной линиями: 1) y = x² – 8x + 16; y = 6 – x 2) 3) у = х2 – 2 (х≥0), у = – 1, у = 7, х = 0
4. Найти объем тела, образованного вращением вокруг оси Оу кубической параболы
ВАРИАНТ 2 1. Вычислить работу, совершенную при растяжении пружины на 6 см, если длясжатия ее на 3 см нужно приложить силу 15 Н.
2. Скорость точки, движущейся прямолинейно, задана уравнением v = 6t²– 4t – 10, см/с. Вычислить: путь, пройденный точкой за первые 4 секунды движения; путь, пройденный точкой за четвертую секунду движения.
3. Найти площадь фигуры, ограниченной линиями: 1) y = x² – 6x + 9; 3x – y – 9 = 0 2) 3) 4. Вычислить объем тела, полученного от вращения вокруг оси Ох трапеции, образованной прямыми
ВАРИАНТ 3 1. Вычислите работу, совершаемую при сжатии пружины на 0,05 м, если для ее сжатия на 0,02 м нужна сила в 10 Н.
2. Скорость точки, движущейся прямолинейно, задана уравнением v = 3t² – 2t – 1, м/c. Вычислить: путь, пройденный точкой за 5 секунд после начала движения; путь, пройденный точкой от начала движения до ее остановки.
3. Найти площадь фигуры, ограниченной линиями: 1) y = – x² + 6х – 5, y = 0; 2) y2 = x, y = x2 3) у = 16х3, у = 2, осью ординат 4. Вычислить объем тела, полученного от вращения вокруг оси Оу трапеции, образованной прямыми у = 3х, у = 2, у = 4 и осью ординат
ВАРИАНТ 4 1. Вычислить работу, совершенную при сжатии пружины на 6 см, если для растяжения ее на 1 см нужно приложить силу в 10 Н.
2. Скорость точки, движущейся прямолинейно, задана уравнением v=24t – 6t²¸ м/с. Вычислить: путь, пройденный точкой от начала движения до ее остановки; путь, пройденный точкой за вторую секунду движения.
3. Найти площадь фигуры, ограниченной линиями: 1) у = х2 + 1, у = 2х + 9, х = 0, у = 0 2) 3) x + 2y - 8 = 0, у = 1, у = 3 4. Криволинейная трапеция, ограниченная гиперболой
ВАРИАНТ 5 1. Вычислить работу, которую нужно затратить, чтобы растянуть пружину на 6 см, если сила 1 Н растягивает ее на 1 м.
2. Скорость движения точки меняется по закону v = 4t – t2, где v – скорость, м/с; t – время, с. Вычислить: путь, пройденный точкой за первые 3 секунды движения; путь, пройденный точкой от начала движения до ее остановки.
3. Найти площадь фигуры, ограниченной линиями: 1) y = x² – 2x + 3, y = x+3 2) у3 = х, у = 1, х = 8 3) 4. Найти объем тела, полученного от вращения кривой Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Поиск по сайту: |
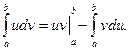

 ,
,  ; тогда
; тогда  ,
,  . Подставив в формулу интегрирования по частям, получим
. Подставив в формулу интегрирования по частям, получим .
. х = -3, х = – 1, осью абсцисс
х = -3, х = – 1, осью абсцисс в пределах от у = 1 до у = 8
в пределах от у = 1 до у = 8 ,
, 
 , у = 1, у = 0, х = 0
, у = 1, у = 0, х = 0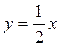 , х = 4, х = 6 и осью абсцисс
, х = 4, х = 6 и осью абсцисс ,
,  , х = 1
, х = 1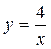 и прямыми х = 3, х = 12 вращается вокруг оси Ох. Найти объем тела вращения.
и прямыми х = 3, х = 12 вращается вокруг оси Ох. Найти объем тела вращения. , у = 1, у = 4, осью ординат
, у = 1, у = 4, осью ординат вокруг оси Оу в пределах от у = 1 до у = 5
вокруг оси Оу в пределах от у = 1 до у = 5