 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Практическое занятие №24
Наименование занятия: Вычисление двойных интегралов Цель занятия:Научиться вычислять двойные интегралы. Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции нескольких действительных переменных». Литература:
Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Двойные интегралы
Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0.
0 x
Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область D. С геометрической точки зрения D - площадь фигуры, ограниченной контуром. Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dхi, а по оси у – на Dуi. Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны Si = Dxi × Dyi . В каждой частичной области возьмем произвольную точку Р(хi, yi) и составим интегральную сумму
где f – функция непрерывная и однозначная для всех точек области D. Если бесконечно увеличивать количество частичных областей Di, тогда, очевидно, площадь каждого частичного участка Si стремится к нулю. Если при стремлении к нулю шага разбиения области D интегральные суммы
С учетом того, что Si = Dxi × Dyi получаем:
Вычисление двойного интеграла
Поиск по сайту: |
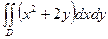









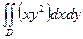
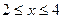





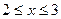





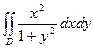

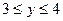

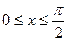







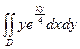





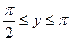








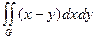 G: x = 0, y = 0, x + y = 2
G: x = 0, y = 0, x + y = 2
 G: x = 1, y = х2, y =
G: x = 1, y = х2, y = 
 G: x = 1, y = -х3, y =
G: x = 1, y = -х3, y = 
 G: y = 0, y = x, х = 1
G: y = 0, y = x, х = 1
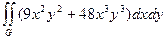 G: x = 1, y = -х2, y =
G: x = 1, y = -х2, y =  G: x = 1, y = х3, y =
G: x = 1, y = х3, y = 
 G: x = 1, y = х3, y =
G: x = 1, y = х3, y =  G: x = 1, y = -х2, y =
G: x = 1, y = -х2, y =  G: y = х3, x = 0,x + y = 2
G: y = х3, x = 0,x + y = 2
 G: x = 1, y = -х3, y =
G: x = 1, y = -х3, y =  G: y = 0, y = cos x, y = x + 1
G: y = 0, y = cos x, y = x + 1
 G: x = 1, y = х2, y =
G: x = 1, y = х2, y =  G: x = 1, y = -х2, y =
G: x = 1, y = -х2, y = 
 y
y
 имеют конечный предел, то этот предел называется двойным интеграломот функции f(x, y) по области D.
имеют конечный предел, то этот предел называется двойным интеграломот функции f(x, y) по области D.
