 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Практическое занятие №20
Наименование занятия: Вычисление определенных интегралов Цель занятия:Научиться вычислять определенные интегралы Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной» Литература:
Задание на занятие:
Вычислить определенные интегралы
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Приращение F(b) – F(a) любых из первообразных функций F(x) + С при изменении аргумента от х=а до х=b называется определенным интегралом от функции f. Вычисляется определенный интеграл по формуле Ньютона – Лейбница:
Свойства определенного интеграла 1) При перестановке пределов изменяется знак интеграла:
2) Интеграл с одинаковыми пределами равен нулю:
3) Отрезок интегрирования можно разбить на части:
4) Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов 5) Постоянный множитель можно вынести за знак определенного интеграла.
Пример 1. Вычислить определенный интеграл Решение. Применяя формулу Ньютона-Лейбница и свойства определенного интеграла, получим:
Замена переменной в определенном интеграле Пусть задан интеграл Введем новую переменную в соответствии с формулой x = j(t). Тогда если 1) j(a) = а, j(b) = b 2) j(t) и j¢(t) непрерывны на отрезке [a, b] 3) f(j(t)) определена на отрезке [a, b], то
Пример 2. Решение. Выполним замену (аналогично замене переменной в неопределенном интеграле): Введем новые переменные интегрирования. Полагая х = 0 и х = 4, подставим их в замену и получим t = 9 и t = 25. Следовательно,
Поиск по сайту: |
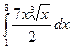
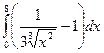
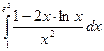
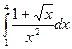
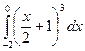
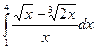
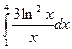
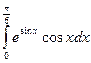
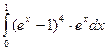
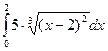
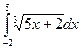
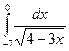
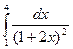
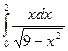
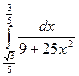
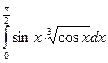
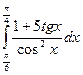
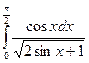
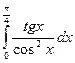
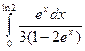
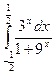
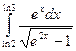
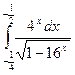
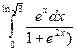
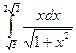
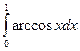
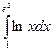
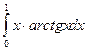
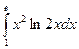
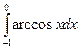
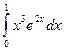
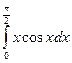
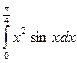
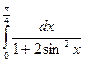
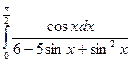
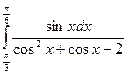
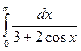
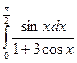
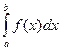= F(b) – F(a)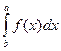
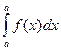= 0
+ 
= 
- 
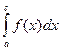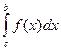
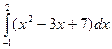
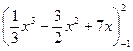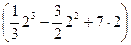= 19,5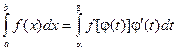
; 
; 
.
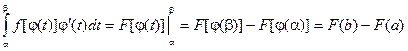
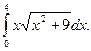
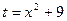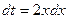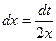