 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
СЛУЧАЙ 2. Выборки зависимые
Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей. Такая задача возникает, когда имеются данные об изменении интересующего признака у каждого пациента. Например, если группа пациентов получала изучаемый метод лечения, и у каждого пациента измерялось значение признака до и после лечения. В данном случае предстоит проверить нулевую гипотезу о равенстве нулю изменений этого признака в результате получения терапии. При подобных исследованиях все наблюдения можно представить в виде n-пар измерений (например, до и после) Для каждой пары вычисляется разность di, где i=1, n Для полученного ряда вычисляется среднее Далее вычисляется значение критерия Стъюдента
Проверка гипотезы производится по таблицам распределения Стьюдента (Приложение 2) для выбранного уровня значимости и числа степеней свободы f= п-1. Если │tвыч │<tкрит то принимается Н(0)
Если │tвыч│≥tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями «до» и «после».
Контрольное задание 5: 1. На каком уровне значимости можно утверждать, что содержание сахара в крови лиц основной и контрольной групп одинаково
Таблица 19. Данные к заданию
2. По данным из таблицы 20 сформулируйте нулевую и альтернативную гипотезы. Какая из гипотез будет принята. Таблица 20. Данные к заданию
Поиск по сайту: |
 и среднеквадратичное отклонение
и среднеквадратичное отклонение 
 (15)
(15) (уд/мин)
(уд/мин)
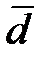 (уд/мин)
(уд/мин)