 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методы простой экстраполяции
Метод среднего уровня ряда – прогнозируемый уровень изучаемой величины принимается равным среднему значению уровней ряда этой величины в прошлом. Этот метод используется, если средний уровень не имеет тенденции к изменению, или это изменение незначительно (нет явно выраженного тренда, рисунок 32А)
Где yi – значение iого уровня n – база прогноза В некотором смысле отрезок динамического ряда, охваченный наблюдением, можно уподобить выборке, а значит полученный прогноз будет выборочным, для которого можно указать доверительный интервал
где – среднеквадратичное отклонение временного ряда
tα –критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n1).
Метод скользящих средних– метод прогнозирования на краткосрочный период, основан на процедуре сглаживания уровней изучаемой величины (фильтрации). Преимущественно используются линейные фильтры сглаживания с интервалом m т.е.
Доверительный интервал
Где
tα –критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n1).
Метод экспоненциального сглаживания –в процессе выравнивания каждого уровня используются значения предыдущих уровней, взятых с определенным весом. По мере удаления от какогото уровня вес этого наблюдения уменьшается. Сглаженное значение уровня на момент времени t определяется по формуле
где St – текущее сглаженное значение; yt – текущее значение исходного ряда; St – 1 – предыдущее сглаженное значение; α сглаживающая параметр S0 берется равным среднему арифметическому нескольких первых значений ряда Для расчета α предложена следующая формула
По поводу выбора α нет единого мнения, эта задача оптимизации модели пока еще не решена. В некоторых литературных источниках рекомендуется выбирать 0,1 ≤ α ≤ 0,3. Прогноз рассчитывается следующим образом
Доверительный интервал
Рассмотренные методы прогнозирования являются простейшими, и в тоже время самыми приближенными – это видно из широких доверительных интервалов в приведенных примерах. Большая погрешность прогноза наблюдается в случае сильных колебаний уровней. Также неправомерно использовать эти методы при наличии явной тенденции к росту (или падению) исходного временного ряда. Но все же для краткосрочных прогнозов их применение бывает оправданным.
Поиск по сайту: |
 (59)
(59)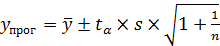 (60)
(60)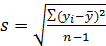 (61)
(61) (62)
(62) (63)
(63)
 (65)
(65)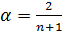 (66)
(66)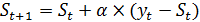 (67)
(67) (68)
(68)