 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
СЛУЧАЙ 1. Выборки независимые
В этом случае нулевая гипотеза Н(0) звучит так: • две генеральные средние равны • или - две выборки извлечены из одной генеральной совокупности • или - две совокупности имеют одинаковое распределение В медицинских задачах гипотеза может быть сформулирована, например, таким образом: содержание гемоглобина у городских и сельских жителей одинаково (подразумевая, что одинаково его распределение). Проверяемый t-критерий вычисляется по формуле
где m1, m2 - стандартные ошибки средних значений сравниваемых выборок.
Находим по таблице tкрит для заданного α и числа степеней свободы f =n1 + n2 – 2 (12)
Если │tвыч │<tкрит то принимается Н(0) (нет аргументов, чтобы ее отвергнуть)
Если │tвыч│≥tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями на соответствующем уровне значимости. Условие равенства двух генеральных дисперсий проверяется по критерию Фишера, который равен отношению большей выборочной дисперсии к меньшей:
Fкрит находится по таблице (Приложение 7) для заданного αи числа степеней свободы f1=n1-1 и f2=n2-1 (14) Если Fвыч≥ Fкрит , то гипотеза о равенстве генеральных дисперсий отвергается
Если Fвыч< Fкрит , то принимается нулевая гипотеза о равенстве.
Поиск по сайту: |
 (11)
(11) – выборочные средние
– выборочные средние (13)
(13)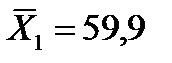

 (мг%)
(мг%)