 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Поставленную задачу можно сформулировать следующим образом: определить влияние многоуровневого фактора на случайную величину. Рассмотрим более простой случай - влияние рациона питания на привес животных. Было проведено исследование на 4 группах животных: первая группа потребляла обычный рацион, вторая – питалась только макаронами, третья – мясом, четвертая – овощами. Изучаемым фактором является рацион питания, который имеет четыре уровня, случайная величина – это привес животных. Нужно определить есть ли разница хотя бы между двумя средними в этих группах. Прежде чем приступить к решению данной задачи, вспомним, что дисперсия является характеристикой разброса случайной величины относительно среднего. В идеале, внутри каждой группы вес животных должен бы быть одинаковым, так как они питаются одинаковым рационом (например, все едят овощи). В реальности внутри групп будет наблюдаться разброс в привесе, в связи с тем, что кроме рациона на вес животных влияют другие факторы: особенности обмена веществ, поведенческих реакций, стрессоустойчивость и др. Эти факторы, которые мы будем называть неучтенными факторами, приводят к появлению внутригрупповой дисперсии Dвнутргр. Средние по группам также имеют разброс (относительно общей средней), который объясняется влиянием изучаемого фактора - разных рационов. Это приводит к появлению межгрупповой дисперсии Dмежгр. Рассмотрим случай, приведенный на рисунке 22. Видно, что внутри групп разброс показателя веса больше, чем разброс средних значений по группам. Можно предположить, что вес животных в этих группах не сильно зависит от рациона питания, а на него больше влияют неучтенные в данном исследовании факторы.
Рисунок 22. Внутригрупповая дисперсия
Другой случай представлен на рисунке 23.
Рисунок 23. Межгрупповая дисперсия
Таким образом, чтобы оценить влияние многоуровневого фактора на какую-то величину, необходимо сопоставить межгрупповую и внутригрупповую дисперсии. Межгрупповая дисперсия вносится изучаемым фактором, внутригрупповая дисперсия вносится какими-то другими (неучтенными) факторами. Если Если Если Мы бы воспользовались этим правилом, если бы нам была доступна генеральная совокупность, но выборочные данные, в том числе выборочные дисперсии, ошибочны и в этом случае необходимо прибегнуть к теории проверки статистических гипотез. Выдвигаем Н(0) – фактор не влияет на изучаемый признак Задаемся уровнем значимости α Вычисляем выборочную внутригрупповуюдисперсию, как среднее значение дисперсий по группам
Где Ивыборочную межгрупповую дисперсиюкак отклонение средних в каждой группе от общей средней
ni –количество объектов в i –той группе
Вычисляем критерий Фишера
Сравниваем с
где k – число групп, n-общее количество объектов обследования
Если вычисленное значение критерия Фишера меньше критического, то Н(0) принимается и делается вывод, что фактор не влияет на исследуемый показатель. В противном случае принимается Н(1).
Контрольное задание 11: Используя факторный дисперсионный анализ определить, отличается ли число тромбоцитов у детей разного возраста:
Таблица 50. Данные к заданию
ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
Обратимся к диаграмме на рисунке 24, на которой представлены значения роста и веса 14 испытуемых, отложенные на соответствующих осях, а на их пересечении поставлены точки. Эта диаграмма носит название диаграммы рассеяния. Из нее видно, что при увеличении роста вес также увеличивается, хотя это бывает не всегда – из практики мы знаем, что встречаются маленькие полные и высокие худые люди. Но общая тенденция все же такая, и мы можем даже провести воображаемую линию, по которой происходят изменения. То есть между ростом и весом имеется определенная связь – изменение роста приводит к изменению веса, и эта связь носит линейный характер.
Рисунок 24. Зависимость веса от роста Степень выраженности связи между случайными величинами отражает понятие корреляция. Количественно взаимосвязь между случайными величинами определяет коэффициент корреляции – r. • Коэффициент корреляции лежит в пределах -1 ≤ r ≤ 1. • Если r> 0, то связь прямая - с увеличением значений одной величины другая также в среднем возрастает. • Если r < 0, то связь обратная - с увеличением величины Х1 соответствующие им значения X2 в среднем также уменьшаются. Значения линейного коэффициента корреляции и характер связи приведены в таблице 51
Таблица 51. Значения коэффициента корреляции
Оценить корреляцию между признаками можно и по диаграмме рассеяния. Чем ближе точки на графике к прямой линии, тем больше коэффициент корреляции (рисунок 25).
Рисунок 25. Диаграммы рассеяния
При прямой связи воображаемая линия направлена слева на право вверх, при обратной – слева на право вниз. В случае r = ±1 все точки диаграммы лежат на одной прямой линии – значит одна величина на сто процентов зависит от другой.Корреляция может быть и нелинейной как это видно из рисунка 26, на котором отражена зависимость ЧСС от возраста.
Рисунок 26. Нелинейная корреляция
Надо помнить, что корреляция выражает лишь математическую связь и, опираясь только на него, нельзя делать выводы о причинно-следственных отношениях. Например, может получиться высокий коэффициент корреляции между массой тела и знанием биостатистики, однако вряд ли одно является следствием другого, возможно оба признака меняются под воздействием третьего – возраста человека. В статистике используются параметрические и непараметрические коэффициенты корреляции. Для двух количественных случайных величин Х1 и Х2 (n -объем каждой выборки), если они нормально распределены, их линейную взаимосвязь можно вычислить используя параметрический коэффициент корреляции Пирсона
Одной из задач корреляционного анализа является проверка коэффициента корреляции на значимость. Дело в том, что выборочный коэффициент корреляции отличается от генерального, т.е. имеет определенную ошибку. При этом не исключена возможность, что взаимосвязь между величинами вовсе отсутствует. Поэтому требуется проверка нулевой гипотезы о равенстве нулю генерального коэффициента корреляции Н(0): r=0
Проверяется гипотеза по критерию Стъюдента:
Критическое значение критерия находится по таблице для заданного уровня значимости α и числа степеней свободы f=n-2 (Приложение 2). Если │ tвыч│≥ tкрит то принимается Н(1) и делается вывод, что между величинами существует значимая корреляция. Если │ tвыч│< tкрит то принимается Н(0) и делается вывод о независимости исследуемых величин (коэффициент корреляции незначим). Полезно также вычислять величину r2 (в %). Она показывает, какая доля изменчивости одной величины объясняется влиянием другой величины.
Поиск по сайту: |
 то фактор не влияет
то фактор не влияет то фактор влияет
то фактор влияет то неопределенность
то неопределенность (43)
(43) - дисперсия показателя в каждой из kгрупп
- дисперсия показателя в каждой из kгрупп (44)
(44) - общая средняя
- общая средняя (45)
(45) (Приложение 7) для заданного α и числа степеней свободы
(Приложение 7) для заданного α и числа степеней свободы
 (46)
(46)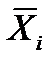
 66,9
66,9



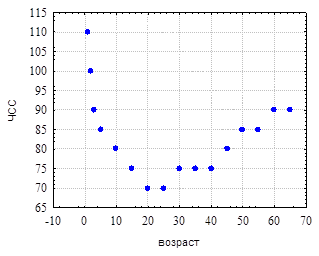
 (47)
(47) (48)
(48)