Проверка гипотезы о нормальности распределения случайной величины

Гистограмма, построенная по выборочным данным, и ее огибающая дают нам лишь качественное (несколько искаженное) представление о законе распределения случайной величины. Для более точной оценки «нормальности» распределения можно использовать показатели, характеризующие форму кривой.

Коэффициент ассиметрииAs – показатель отклонения кривой распределения от симметричности.

(9)

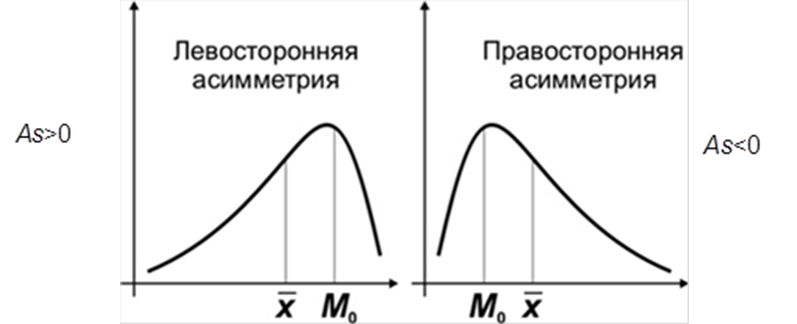
Как видно из рисунка 15 отрицательный коэффициент ассиметрии означает, что кривая распределения скошена влево от центра, положительный – вправо. При нормальном распределении As близок к нулю.

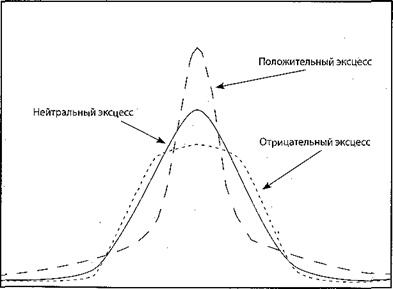
Рисунок 15. Ассиметрия

Коэффициент эксцессаEx характеризует степень заостренности кривой распределения (положительный коэффициент свидетельствует о об более острой вершине, отрицательный – о более пологой).

(10)

Рисунок 16. Эксцесс

Для нормального распределения эти коэффициенты должны быть близки к нулю. Но, поскольку они являются выборочными, то на практике точное равенство нулю почти не встречается. Поэтому для проверки нормальности распределения рекомендуется использовать соответствующие таблицы (Приложение 1), в которых указаны критические точки для этих коэффициентов при различных уровнях значимости и объемах выборки. Если рассчитанное значение для ассиметрии или эксцесса по модулю превосходят эти критические точки, то нулевая гипотеза о нормальности распределения отвергается, в противном случае - принимается.

Пример.Проверить на нормальность распределения систолического артериального давления по выборке из 25 значений. 108, 115, 133, 102, 110, 118, 118, 120, 120, 127, 127, 127, 110, 100, 105, 120, 120, 130, 135, 140, 135, 146, 145, 160, 155 Н(0): распределение систолического давления соответствует нормальному распределению Таблица 12. Результаты статобработки   п =25 125,04 s=15,9 As=0,424 Ex=-0,655 α=0,05 As крит=0,711 Exкрит=0,869   Поскольку вычисленные значения коэффициентов меньше соответствующих табличных (Приложение 1), то принимается нулевая гипотеза.

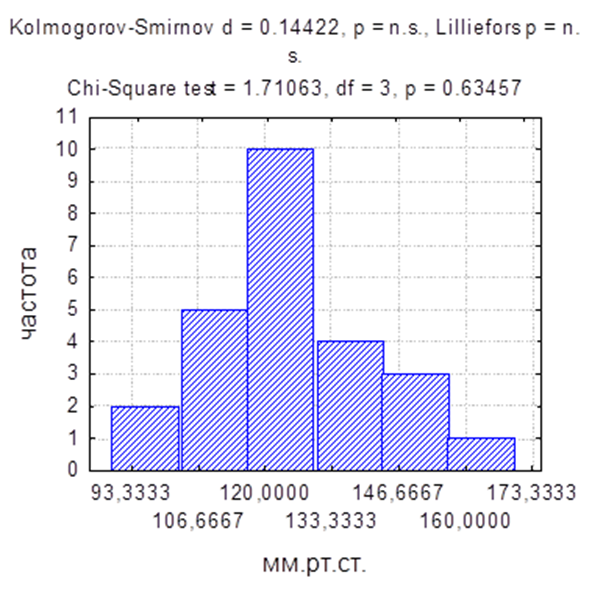
Проверка гипотезы о нормальности распределения может быть осуществлена и на основе других критериев: хи-квадрат, Колмогорова-Смирнова, Шапиро-Уилкса. Эти процедуры заложены во многих пакетах статистического анализа. Ниже приведены результаты обработки данных в ППП STATISTICA (Рисунок 17).

Рисунок 17. Проверка на нормальность распределения

По критерию Колмогорова-Смирнова получен результат n=n.s. (отличие от нормального статистически незначимо), по критерию хи-квадрат р=0,63, что также указывает на статистическую незначимость отличий распределения давления от нормального.

Контрольное задание 4:

По данным из таблицы 13 проверить нулевую гипотезу о нормальности распределения случайной величины

Таблица 13. Данные к заданию

п =50

4,43

s=1,25

α=0,05

As=0,655

Ex=-0,901

Поиск по сайту: