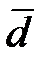|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Доверительный интервал для разности генеральных средних двух независимых групп
Если разность двух генеральных средних оценивается по выборкам, то она, эта разность, является случайной величиной и имеет ошибку (Рисунок 21). Для генеральной разницы также можно указать доверительный интервал. Для этого сначала надо вычислить объединенное среднеквадратичное отклонение:
Тогда доверительный интервал находится в пределах
от
где t – критическое значение двустороннего t-критерия Стъюдента для заданного α и (п1+ п2-1) степеней свободы.
Рисунок 21. Ошибка генеральной разности Интерпретация. · Если доверительный интервал для разности средних включает в себя ноль, то принимается нулевая гипотеза о равенстве двух генеральных средних. · Верхний и нижний предел доверительного интервала для разности может быть использован для клинической оценки разности двух средних.
Доверительный интервал для разности генеральных средних двух зависимых групп При сравнении одних и тех же объектов «до» и «после» оценивается средняя разность Доверительный интервал генеральной средней разности лежит в пределах
от
где t – критическое значение двустороннего t-критерия Стъюдента для заданного α и (п-1) степеней свободы. Интерпретация. · Если доверительный интервал для средней разности включает в себя ноль, то принимается нулевая гипотеза о равенстве двух генеральных средних. · Верхний и нижний предел доверительного интервала для разности может быть использован для клинической оценки разности двух средних.
Поиск по сайту: |
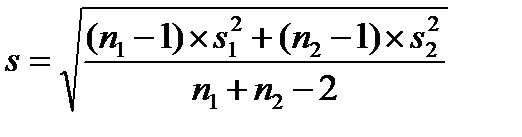 (21)
(21)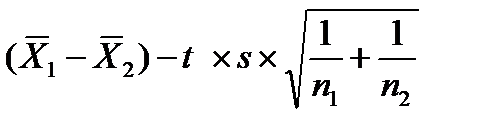 до
до 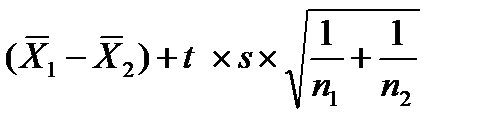 (22)
(22)
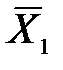
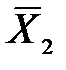
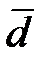 значений признака, измеренного «до» и «после», а также среднеквадратическое отклонение этих разностей sd .
значений признака, измеренного «до» и «после», а также среднеквадратическое отклонение этих разностей sd . до
до 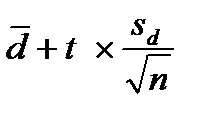 (23)
(23)