 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
АНАЛИЗ МЕДИКО-БИОЛОГИЧЕСКИХ ДАННЫХ НА ОСНОВЕ ИХ ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ
Вернемся к примеру с анализом роста в группе людей. Если группа достаточно большая, то мы получим очень большой ряд данных: 175, 172, 180, 188, 166, 168, 170, 175, 178, 182, 188, 169 175, 172, 180, 188, 166, 168, 170, 175, 178, 182, 188, 169 175, 172, 180, 188, 166, 168, 170, 175, 178, 182, 188, 169……… и затруднимся дать обобщающую характеристику этой совокупности. Для более наглядного представления данных обычно используются графики, рисунки, диаграммы, таблицы. Воспользуемся подобным методом и мы – разобьем весь диапазон роста от минимума до максимума на равные интервалы по 10 см и посчитаем сколько объектов попадет в каждый из этих интервалов (частоту встречаемости), а затем построим график, как показано на рисунке 6А – по оси абсцисс отложим интервалы, а по оси ординат – частоту встречаемости (абсолютную или относительную в %). Полученный график называется гистограммой распределения, он показывает, насколько часто встречаются те или иные значения изучаемой случайной величины (его вероятность), в данном случае роста, или другими словами как рост распределен по различным диапазонам. Теперь по этому графику попытаемся дать обобщенную характеристику изучаемой группе.
Минимальный рост лежит в пределах от 140 до 150 см, самые высокие имеют рост 190-200 см. Наиболее часто встречается средний рост (170-180 см) в 25% всех случаев. По мере удаления от среднего роста в меньшую и большую сторону частота встречаемости снижается. Низкорослые и высокие встречаются реже, чем лица среднего роста. Самые маленькие (140-150 см) составляют 10% совокупности, самые высокие (190-200 см) - 12%. Представим, что количество обследованных бесконечно увеличивается, а длина интервалов бесконечно уменьшается, тогда мы получим график, который изображен на рисунке 6 в виде огибающей гистограммы. Это кривая дает нам представление о законе распределения случайной величины (иногда говорят просто распределение). Она может иметь различную форму. Распределение многих случайных величин имеет симметричный колоколообразный вид, и такое распределение называется нормальным (еще его называют Гауссовским распределением). Нормальное распределение имеет важное значение в статистике, поскольку обладает рядом замечательных свойств, о которых мы поговорим позже. Кроме нормального существуют и другие виды распределения. Так, форма гистограммы, представленной на рисунке 6Б, явно не соответствует колоколообразному виду. В статистике широко используются биноминальное, логарифмическое, хи-квадрат распределения, распределения Стъюдента, Фишера и др. Надо отметить, что оценка закона распределения по кривой огибающей гистограммы является не совсем корректной, качественной, учитывая также и то, что гистограмма строится по ограниченным выборочным данным. Существуют специальные статистические процедуры и критерии, которые позволяют строго количественно оценить закон распределения. Им будет посвящена специальная глава. В медицинских исследованиях при построении гистограмм длительность интервалов может быть не одинаковой, а их границы заранее оговорены. Например, в возрастной физиологии приняты следующие возрастные периоды, приведенные в таблице 1.
Таблица 1. Возрастные периоды
При анализе частоты пульса возможны такие интервалы: меньше 60 уд/мин, 60-80 уд/мин, больше 80 уд/мин.
Опишите гистограмму с указанием: · общего количества обследованных. · минимального и максимального значения анализируемой величины, (с указанием % случаев) · наиболее часто и редко встречающегося значения анализируемой величины (с указанием % случаев) .
Поиск по сайту: |


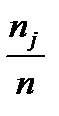 и процент случаев
и процент случаев  .
.