 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
СЛУЧАЙ 2. Выборки зависимы
Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей. Такая задача возникает, когда имеются данные об изменении интересующего признака у каждого пациента. Например, если группа пациентов получала изучаемый метод лечения и у каждого пациента измерялось значение признака до и после лечения. В данном случае предстоит проверить нулевую гипотезу о равенстве нулю среднего изменения этого признака в результате получения терапии. При подобных исследованиях все наблюдения можно представить в виде n-пар измерений (например, до и после) Для каждой пары вычисляется разность di, i=1, n Для полученного ряда вычисляется среднее
Критерий Стъюдента определяется по формуле
tкрит находится по таблице для заданного α и числа степеней свободы f =n-1
Если │tвыч │<tкрит то Н(0)
Если │tвыч│≥tкрит то Н(1) и делается заключение о наличии статистически значимых различий между средними значениями «до» и «после» на соответствующем уровне значимости. · Доверительный интервал для разницы генеральных средних двух зависимых групплежит в пределах от
где t – критическое значение двустороннего t-критерия Стъюдента для заданного α и (п-1) степеней свободы. Работа с преподавателем.В группе из 6 больных гипертонией изучалось влияние лекарственного препарата, снижающего артериальное давление. В результате опыта получилось 2 вариационных ряда систолического давления: первый – до приема препарата, второй – после приема: Таблица 1.
Определить, изменяется ли в генеральной совокупности систолическое артериальное давление после приема препарата и насколько статистически значимы полученные результаты, если известно,что данные имеют нормальное распределение и две генеральные дисперсии равны? Для наглядности представим данные в следующей таблице: Таблица 2.
Н(0): Н(1):
Для разностей давлений:
Определим tвыч:
Определим по таблице Стьюдента tкрит для α=0,05 и числа степеней свободы f=n-1= tкрит= (двусторонний критерий). Вывод:
Сведем результаты расчетов в таблицу
Определим доверительный интервал для средней разницы двух зависимых групп. .
Контрольные вопросы 1. Основные задачи биостатистики 2. Генеральная совокупность и выборка. Какие бывают выборки. 3. Понятие распределения, нормальное распределение и его свойства 4. В каком случае две совокупности считаются не отличающимися по данному признаку 5. При каких условиях две нормально распределенные совокупности не отличаются по данному признаку. 6. Понятие статистических гипотез 7. Как проверяются гипотезы 8. Уровень значимости и достигнутый уровень значимости 9. Виды критериев, как выбрать критерий 10. Какие гипотезы проверяются при помощи критерия Стъюдента 11. Понятие доверительного интервала 12. Интерпретация доверительного интервала
Контрольное задание:
Поиск по сайту: |
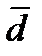 и среднеквадратичное отклонение
и среднеквадратичное отклонение 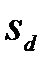 , стандартную ошибку средней
, стандартную ошибку средней 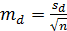
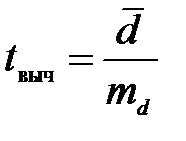
 до
до 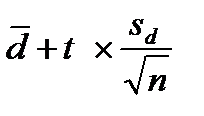
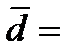
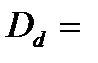
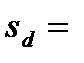
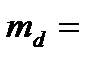
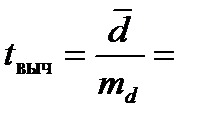
 (мм.рт.ст.)
(мм.рт.ст.)
 (мм.рт.ст.)
(мм.рт.ст.)