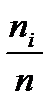Работа с преподавателем

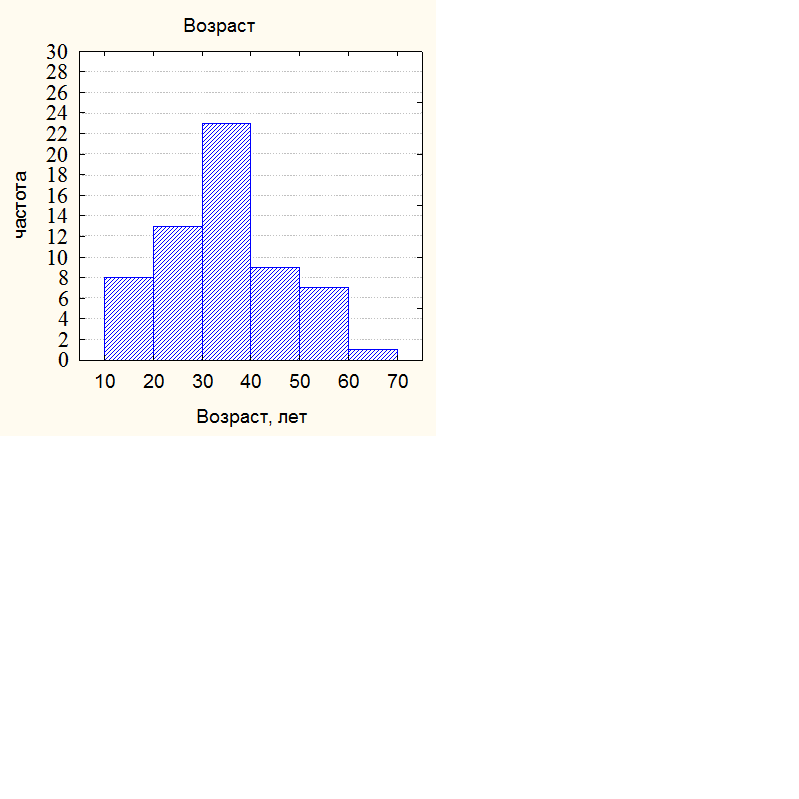
Задача: Даны значения пульса у 25 испытуемых (объем выборки n=25). Представить выборку в виде таблицы частот и построить гистограмму.

70 75 63 64 72 77 80 85 79 64 63 60 55 56 58 58 73 72 65 65 66 68 69 66 68

Необходимо выполнить следующие шаги:

1. Элементы выборки объемом n=25 расположить в ранжированный ряд (по возрастанию или убыванию)

2. Вычислить размах R (разность между минимальным и максимальным значением случайной величины):

R=x_max-x_min=

3. Разбить вариационный ряд на k непересекающихся интервалов. k вычисляют по формуле Стерднесса, предусматривающей выделение оптимального числа интервалов:

k=1+3.322lg(n) (округлить до целого)

Можно воспользоваться следующими рекомендациями

4. Определить длину одного интервала:

b=R/k

5. Определить границы каждого интервала

6. Определить частоты - количество ni элементов выборки, попавших в i-й интервал (элемент, совпадающий с правой границей интервала, относится к последующему интервалу)

Наряду с частотами одновременно подсчитываются также относительные частоты и процент случаев относительно общего объема выборки

Полученные результаты сводятся в таблицу, называемую таблицей частот группированной выборки.

Для нашей задачи результаты группировки представлены в следующей таблице:

Номер интервала, i	Границы интервала	Частота, ni	Относительная частота	Процент случаев
	ИТОГО	Σ=	Σ=	Σ=

7. Далее строится гистограмма. По оси абсцисс откладываются интервалы, по оси ординат могут откладываться абсолютная частота встречаемости, или относительная частота встречаемости, или же процент относительно общего объема выборки.

В данном случае исследуемый признак – это пульс, который является случайной величиной X (x₁, x₂, x₃ …..x_i…… x_n)

Этот график дает нам информацию о законе распределения случайной величины и носит название гистограммы распределения. Он показывает, насколько часто встречаются те или иные значения случайной величины.

По оси ординат могут откладываться

• Абсолютная частота встречаемости

• Процент относительно общего объема выборки

• Относительная частота встречаемости

Огибающая гистограммы дает нам качественное представление о законе распределения случайной величины (иногда просто говорят распределение). Этот закон характеризует вероятность того, что случайная величина примет то или иное значение. Существует множество различных законов распределения. Наиболее распространенным является нормальное распределение – оно имеет симметричный колоколообразный вид.

Какую информацию дает нам этот график.

Самостоятельная работа:Согласно своему варианту для случайной величины из таблицы данных построить гистограмму распределения. Описать полученные результаты.

Задание к ТЕМЕ 1 Опишите приведенную ниже гистограмму с указанием:

· общего количества обследованных.

· минимального и максимального значения анализируемой величины, (с указанием в скольких процентов случаев)

· наиболее часто и редко встречающегося значения анализируемой величины (с указанием в скольких процентов случаев)

· в каких пределах в основном лежит анализируемая величина.

· дайте качественную оценку функции плотности распределения данной случайной величины (нормальное или отличное от нормального).

Контрольные вопросы

1. Основные задачи биостатистики

2. Какую информацию несет гистограмма

3. Что понимается под термином «распределение»

4. Какая величина откладывается по оси ординат при построении гистограммы

5. Какая величина откладывается по оси абсцисс при построении гистограммы

6. Как определяется число интервалов при построении гистограммы

7. Какими свойствами обладает нормальное распределение

8. В каком случае две совокупности считаются не отличающимися по данному признаку

9. При каких условиях две нормально распределенные совокупности не отличаются по данному признаку.

Поиск по сайту: