 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
СРСП 2. Проверка гипотезы о нормальности распределения случайной величины
Для проверки нормальности распределения случайной величины можно использовать коэффициент ассиметрии и коэффициент эксцесса. Коэффициент ассиметрииAs – показатель отклонения кривой распределения от симметричности.
Отрицательный коэффициент ассиметрии означает, что кривая распределения скошена влево от центра, положительный – вправо. При нормальном распределении As близок к нулю. Коэффициент эксцессаEx характеризует степень заостренности кривой распределения (отрицательный коэффициент свидетельствует о об более острой вершине, положительный – о более пологой).
Для нормального распределения эти коэффициенты должны быть близки нулю. Но, поскольку они являются выборочными, то на практике точное равенство нулю почти не встречается. Поэтому для проверки нормальности распределения рекомендуется использовать соответствующие таблицы (Приложение), в которых указаны критические точки для этих коэффициентов при различных уровнях значимости и объемах выборки. · Если оба рассчитанные значение для ассиметрии и эксцесса по модулю меньше этих критических точек, гипотеза о нормальности распределения принимается. · Если хотя бы один коэффициент больше критического значения, то распределение отличается от нормального Пример.Проверить на нормальность распределения систолического артериального давления по выборке из 25 значений. Н(0): распределение систолического давления соответствует нормальному распределению Выполним вычисления
Поскольку вычисленные значения коэффициентов по модулю меньше соответствующих табличных (см. Приложение), то принимается нулевая гипотеза, т.е. распределение соответствует нормальному. Контрольные вопросы 1. Что понимается под термином «распределение» 2. Классификация признаков, к каким признакам применимо понятие распределение 3. Что характеризуют коэффициент ассиметрии и коэффициент эксцесса. 4. Какими свойствами обладает нормальное распределение 5. Как проверить нормальность распределения Задание к СРСП 2. По данным из таблицы построить гистограмму распределения, провести эмпирическую кривую распределения, вычислить коэффициенты ассиметрии и эксцесса, проверить гипотезу о нормальности распределения.
Поиск по сайту: |
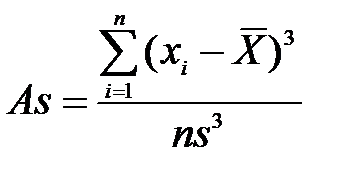
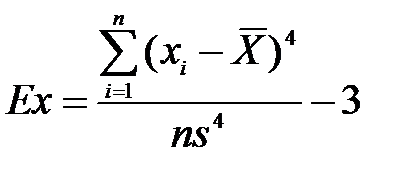
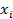
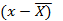
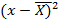
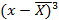
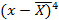
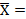 127
127
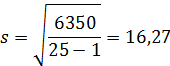


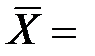 127
127