 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КАК МЕТОД ПОЗНАНИЯСтр 1 из 35Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение Высшего образования «Севастопольский государственный университет» А.Ф. ХРУСТАЛЕВ ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Севастополь 2015
УДК 519.7(075) ББК 22р. я73
Рецензенты: д-р физ.-мат. наук, профессор кафедры физики Севастопольского государственного университета, С.Ф. Барановский; д-р физ.-мат. наук, профессор кафедры высшей математики А.А. Ярошенко. Научный редактор – д-р техн. наук, профессорА.И. Песчанский
Хрусталев А.Ф. Основы математического моделирования: Учеб. пособие. Издание 2-е, переработанное.
Учебное пособие представляет собой авторскую разработку спецкурса по основам математического моделирования, являющегося необходимым компонентом современной подготовки специалистов. В него включены вопросы, связанные с построением и исследованием математических моделей задач, условия которых содержат нематематические понятия. Материал излагается доступно и широко иллюстрируется примерами из химии, физики, географии, экономики и других дисциплин. Книга предназначена широкому кругу научных работников, инженеров и в качестве учебного пособия для аспирантов, студентов и школьников.
ПРЕДИСЛОВИЕ Цель этой книги – изложить в доступной форме для аспирантов, студентов и школьников задачи, методологические принципы и рабочие приёмы научной и учебной дисциплины «математическое моделирование», являющейся необходимым компонентом современной подготовки специалистов. В учебном пособии рассматриваются вопросы построения и исследования математических моделей задач, взятых из химии, физики, экономики, техники, географии и других областей знания. С понятием математической модели по существу знакомы все, и даже те, которые и не пользовались этим термином [40, с.12]. Так, если нужно определить площадь пола комнаты прямоугольной формы, то для выполнения такого задания пол считают прямоугольником, измеряют его длину и ширину, а затем перемножают полученные числа. Вот этот прямоугольник идеализированный, математический вместе с его параметрами: Заметим, что для непосредственного (прямого) измерения указанной площади необходимо иметь, например наборы квадратных плиток со сторонами 1м, 1дм и 1см, которыми можно покрыть весь пол, а затем, пересчитав их, выразить результат в квадратных метрах. Как видим, прямое измерение площади пола даже прямоугольной формы представляет собой непростую задачу. Ясно, что такой способ неприемлем для определения площади большого сельскохозяйственного поля. Поэтому нужна модель, которая дает возможность непосредственно измерить линейные размеры а и b, т.е. использовать результаты более простого эксперимента, и по ним путем умножения найти площадь. Именнотакая мысль нашла отражение в поэме А. С. Пушкина "Борис Годунов": "Учись мой сын: наука сокращает нам опыты быстротекущей жизни... ". Уже из рассмотренного примера видно, что при построении математических моделей используют не материальные предметы, такие как дерево, пластмасса …, а идеализированные, математические объекты: фигуры, уравнения, параметры, произведение, равно, формула и т.п. И вы знаете, что при решении различных задач наиболее часто применяются уравнения и теоремы. Поэтому ДЕВИЗ нашей книги: ПОСРЕДСТВОМ УРАВНЕНИЙ, ТЕОРЕМ МЫ УЙМУ В качестве девиза нами взяты слова отца английской поэзии Джефри Чосера, который, говоря о специалисте, умеющем применять математику, писал: «Посредством уравнений, терем он уйму всяких разрешал проблем: И засуху предсказывал, и ливни. Поистине его познанья дивны». Важной частью пособия является поставленное на стыке фундаментальных дисциплин расчётно-графическое задание по оптимизации. Выполняя это задание, обучающиеся решают не только конкретную задачу, но и, что более важно, убеждаются в справедливости основной теоремы системного анализа: если система состоит из нескольких взаимодействующих между собой подсистем, то оптимум всей системы не определяется оптимумом для каждой из подсистем. Будущие специалисты должны понимать, что системный подход является основой их действий в повседневной жизни. В пособии основное внимание уделено не математическому аппарату, а постановке задач, построению отличных друг от друга математических моделей, их анализу и интерпретации полученных результатов. Поэтому некоторые задачи в нём встречаются более одного раза, но каждый раз создаётся и исследуется другая модель. Для практических приложений важно не единственное решение, полученное на основе анализа одной математической модели, а конкуренция, соперничество, «спор моделей» [3, с. 21]. При этом наибольшего доверия заслуживают те выводы, которые оказываются практически одинаковыми при различных моделях, разных подходах к задаче. Отметим, что пособие существенно опирается на общие вопросы математического моделирования, мастерски изложенные в книгах [3, 6, 29]. В нём также использованы материалы международных студенческих научных конференций, проведенных в Севастопольском национальном техническом университете в 2005 – 2014 годах. Приношу благодарность, студентам, аспирантам, рецензентам, всем своим коллегам, особенно И.А. Меканиной и А.С. Папковой за сотрудничество, полезные советы, замечания и помощь. И, конечно же, автор с благодарностью примет все предложения и пожелания, направленные на совершенствование этой книги.
Сентябрь 2015 г. А.Ф. Хрусталев
Законы природы записаны на языке математики. Г. Галилей ВВЕДЕНИЕ
В параграфе «Зачем нужны модели?» [6, с. 10] сначала приводятся примеры, поясняющие, что такое модель. Когда архитектор готовится построить новое здание, то прежде чем воздвигнуть его, он сооружает здание из кубиков на столе, чтобы посмотреть, как оно будет выглядеть. Это – модель. Если макет того же здания создается с помощью компьютера, то это тоже модель, но в другом исполнении. Если же есть чертеж того же проектируемого здания, то и это – модель и т.д. Таким образом, объект вообще и здание в частности может иметь несколько разных моделей, в зависимости от того, какие и как моделируются его особенности. Для объяснения функционирования системы кровообращения, лектор демонстрирует плакат, на котором стрелочками изображены направления движения крови. Это тоже модель. Какова же их роль и назначение? Конечно, архитектор мог бы построить здание без предварительного рассмотрения его модели. Но он не уверен, что здание будет хорошо смотреться. Уж лучше сначала построить соответствующую модель. «Конечно, лектор мог бы для демонстрации воспользоваться подробным анатомическим атласом. Но и эта подробность ему совершенно не нужна при изучении системы кровообращения. Более того, она мешает изучению, так как отвлекает внимание сосредоточиться на главном. Лучше уж воспользоваться плакатом» [6, с. 10]. В этих примерах некоторый объект сопоставляется с другим объектом, который его заменяет: реальное здание – здание из кубиков; система кровообращения – схема на плакате. И хотя здание из кубиков намного меньше настоящего, оно позволяет судить о внешнем его виде. И хотя плакат и не имеет ничего общего с системами живого организма, но он позволяет судить о том, откуда и куда течет кровь. К этому добавим, что в наше время широко применяются компьютерные средства визуализации процессов моделирования. Прежде всего – это трёхмерная графика и анимация, которые заняли достойное место в создании прототипов и имитации динамики в кино, архитектурных презентациях и других областях, связанных с построением и использованием моделей. Итак, модель – это такой материальный или мысленный объект, который замещает объект-оригинал, сохраняя некоторые важные для понимания и познания типичные егочерты Главное назначение модели состоит в том, что с ее помощью выявляются наиболее существенные свойства исходного объекта, поскольку сама модель отражает лишь некоторые его характеристики. Процесс построения модели называется моделированием. Существуют две основные цели моделирования: научный прогноз и организация разумного поведения. Различают две основные группы моделирования: материальное (предметное) и идеальное. Ко второй относится математическое моделирование, при котором исследование объекта осуществляется посредством модели, сформулированной на языке математики. Ярким примером математического моделирования является описание и исследование основных законов классической механики математическими средствами. Подавляющее большинство будущих специалистов изучают математику для того, чтобы уметь её применять. Но как раз применению математики уделяется очень мало внимания, как в средней, так и в высшей школе. А ведь многие задачи из физики, химии и других дисциплин формулируются на словесном, «гуманитарном», доматематическом уровне, моделируются средствами естественного языка, т.е. задаются в виде текстов, без формул и буквенных обозначений неизвестных и к решению так поставленных задач в первую очередь надо научиться применять математику. Именно такие формулировки задач значительно облегчают построение их математических моделей, поскольку по таким текстам достаточно правильно осуществить перевод условия с обычного языка на язык математических символов, уравнений, неравенств и т.п. и только после этого для решения задачи применять изученный математический аппарат. Итак, математическими методами решают не только абстрактные задачи о геометрических фигурах, числах, уравнениях, дифференциалах…, но и прикладные, условия которых содержат нематематические понятия.
…математика предлагает весьма общие и достаточно четкие модели для изучения окружающей действительности… В. Успенский МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КАК МЕТОД ПОЗНАНИЯ От ясности первого понятия зависит успех всех знаний. Н.И. Лобачевский
Поиск по сайту: |
 – длиной,
– длиной, 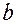 – шириной, формулой для вычисления площади:
– шириной, формулой для вычисления площади:  и есть математическая модель рассматриваемой задачи, а сам прямоугольник – геометрическая модель пола.
и есть математическая модель рассматриваемой задачи, а сам прямоугольник – геометрическая модель пола.