|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие математической модели
Если говорить о познании, то наше время характеризуется проникновением математического образа мышления во все основные сферы. Уже давно существуют такие научные и учебные дисциплины как математическая логика, математическая физика и математическая статистика и относительно недавно, во второй половине XX века, появились новые названия: «математическая экономика», «математическая биология», «математическая лингвистика»... И какую бы науку ни взять, теперь вряд ли кому-нибудь покажется невозможным присоединение к ее наименованию эпитета «математическая» [26, с.5–11]. Теперь уже можно говорить о математизации не только науки, но и жизни, в которую все более активно входит словосочетание «математическая модель». Дело в том, что при решении прикладных задач, т. е. таких, условия которых содержат нематематические понятия, математика применяется не непосредственно к реальному объекту, а к его математической модели [29, с.12], причём термин «объект» понимается в самом широком смысле: это может быть и задача, и процесс, и ситуация, и т.п. Для многих математика стала точным языком выражения мысли, и как литература и искусство, особым способом познания. По аналогии с художественными образами уместно говорить о «математических образах» или более точно и современно о «математических моделях» как форме отражения действительности. И, как, изучая художественные образы, мы познаем отраженную в них жизнь, так исследуя математические модели, мы познаем объективную реальность. Как уже говорилось, с понятием математической модели по существу знакомы все. Так, если нужно определить площадь пола комнаты прямоугольной формы, то для выполнения такого задания пол считают прямоугольником, измеряют его длину и ширину, а затем перемножают полученные числа. Вот этот прямоугольник идеализированный, математический вместе с его параметрами: Ивсе жемы построим здесь такую модель. Но прежде заметим, что для непосредственного измерения указанной площади необходимо иметь, например наборы квадратных плиток со сторонами 1м, 1дм, и 1см, которыми можно покрыть весь пол, а затем, пересчитав их, выразить результат в квадратных метрах. Как видим, прямое измерение площади фигуры в виде прямоугольника представляет непростую задачу в особенности, если нужно найти площадь большого сельскохозяйственного поля даже прямоугольной формы. Вот почему нужна модель, которая дает возможность непосредственно измерить линейные размеры
Рисунок 1.1 из которого очевидно, что площадь квадрата со стороной
Именно с помощью такой модели совсем легко вычислить площадь пола прямоугольной формы: для этого достаточно измерить длину и ширину комнаты, а затем перемножить полученные числа. Заметим, что измерить непосредственно объём прямоугольного параллелепипеда, пользуясь геометрическими моделями соответствующих кубов, ещё сложнее. А по формуле, т.е. косвенно, с помощью математической модели, совсем просто: для этого достаточно измерить длину, ширину и высоту параллелепипеда, а затем перемножить полученные числа. Здесь уместно привести высказывание Д.И. Менделеева: «Наука начинается с тех пор, когда начинают измерять». Итак, с математической моделью связано одно существенное свойство: её участие в эксперименте, в его планировании. В старинной восточной сказке рассказывается: «Царь обещал дать тому, кто взвесит его слона, столько золота, сколько весит сам слон. Бедняк перевозчик ввел слона в свою большую лодку и отметил уровень, до которого она погрузилась в воду. Затем он вывел слона на берег и нагрузил лодку золотом до прежней отметки. Вес золота равнялся весу слона». Теперь осталось взвесить золото частями на весах, допускающих соответствующие нагрузки, и сложить полученные результаты. Вот это арифметическое соотношение, выражающее совсем простую идею, и есть математическая модель, позволяющая косвенно взвесить неделимое тело весом равного груза, который можно взвешивать частями. Чтобы определить сделана ли корона царя Гиерона из чистого золота или ювелир подмешал в неё серебро, Архимед составил следующий план эксперимента. Сначала он сделал слиток из золота того же веса, какой был у короны. Затем наполнил до половины большой сосуд водой, опустил в него золотой слиток и отметил черточкой уровень воды, до которого она поднялась. Вынул золотой слиток и опустил в сосуд корону: черточка соответствующая этому опыту оказалась значительно выше отмеченной. Итак, объем слитка золота оказался меньше объема короны того же веса. Так, с помощью модели в виде неравенства, ювелир был уличен в мошенничестве. Отметим, что координатная или числовая ось, с которой мы познакомились ещё в школе, является в частности математической моделью хронологии исторических событий, причём её отрицательная полуось отражает события, происшедшие до н.э., положительная – моделирует хронологию событий н.э., а начало координат соответствует Рождеству Христову. А математическая модель, представляющая золотую пропорцию (деление отрезка в среднем и крайнем отношении) широко применяется в живописи и архитектуре при создании целостной гармонической формы, наиболее полно выражающей содержание произведения [18, с. 6]. На карте автомобильных дорог, которой пользуются водители, путь от Москвы до Севастополя представляет ломаную линию, состоящую из криволинейных или прямолинейных отрезков. Это – графическая (геометрическая) модель дороги. Можно построить и математическую (аналитическую) модель той же дороги, представив ломаную линию в виде совокупности систем, состоящих из уравнений и неравенств. Но и эта модель лишь приближенно будет отображать реальную дорогу. А вот как определяет обсуждаемое понятие академик А.Н. Тихонов: «Математическая модель –приближенное описание какого – либо класса явлений внешнего мира, выраженное с помощью математической символики» (МАТЕМАТИЧЕСКАЯ ЭНЦИКЛОПЕДИЯ. – М.: СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, 1982.– Т. 3, С. 574)
Поиск по сайту: |
 – длиной,
– длиной, 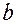 – шириной, формулой для вычисления площади:
– шириной, формулой для вычисления площади:  и есть математическая модель рассматриваемой задачи.
и есть математическая модель рассматриваемой задачи. и
и  и по ним уже математически найти площадь.
и по ним уже математически найти площадь. При построении такой модели будем исходить из того, что площадь квадрата со стороной
При построении такой модели будем исходить из того, что площадь квадрата со стороной  . Теперь получим формулу для определения площади прямоугольника со сторонами
. Теперь получим формулу для определения площади прямоугольника со сторонами  равна сумме площадей квадратов со сторонами
равна сумме площадей квадратов со сторонами  , а потому имеем уравнение:
, а потому имеем уравнение:  , из которого находим:
, из которого находим: