 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Адаптивна система управління на базі НМ персептронного типу
w1 w2 e2 p x
u y - + U
y T - + e1
Рис.9.4. Структура системи
w1, w2 – векторні коефіцієнти зв’язку; Т (target) – завдання; НР – нейромережовий регулятор; НІ – нейромережовий ідентифікатор; ОУ – об’єкт; Р – дані прогнозів. Система відпрацьовує завдання Т. Нейромережовий регулятор НР на основі кінцевої послідовності попередніх значень сигналу похибки управління e1=Т–У та даних прогнозу р формує u. Нейромережовий ідентифікатор НІ обробляє сигнали u і у та формує вихідний сигнал х, який порівнюється з у. Оптимізатори 01 і 02 в процесі навчання НМ обробляють сигнали помилки e1=Т–У і e2=У–Х (управління та ідентифікації), визначають векторні коефіцієнти зв’язку w1 і w2 нейронних мереж НР і НІ. В результаті навчання формуються структура нейрорегулятора НР і модель об’єкта. Багатошарова НМ за топологією - дискретна решітка з визначеними числами шарів і нейронів в кожному з них. Конфігурація мережі обирається з урахуванням складності розв’язуваної задачі. Для опису нейронів використовується функціональна модель: Уі m=f (Zi m), і=1,...s; m=1,...n (9.13) Zi m= Уі m – вихідна величина m-го нейрона в і-му шарі; Zi m – величина внутрішнього стану активності на вході m-го нейрона в і-му шарі; Уі k – вихідна величина k-го нейрона попереднього j-го шару; Wijmk – коефіцієнт зв’язку між m-м та k-м нейронами відповід-них шарів; S – кількість шарів; n – число нейронів в шарі; f (× ) – нелінійна функція перетворення (функція активації), наприклад логістичного типу: у=р1| (1+exp (- p2 (z – p3))|, р1 > 0, p2 > 0 (9.14) р1 – параметр, який визначає максимальний рівень активності на виході нейрона; р2 – параметр крутизни логіста; р3 – параметр крутизни зсуву. Залежність (9.13) в спрощеному вигляді описує механізм синаптичного зв’язку між нейронами. ММ нейронної мережі в цілому опи-сується у вигляді узагальненого ряду Колмогорова-Габара – дискретний аналог нелінійного інтегрального оператора Вольтерра. Для НМ (рис.9.4) модель має вигляд:
U[t] – значення виходу НР в поточний дискретний момент часу t; e[t-i] – значення помилки управління в попередній момент часу [t-i]-й; m – число інтервалів часу; аі, aij, аijk – коефіцієнти ряду, які залежать від дискретних пара-метрів конфігурації мережі і коенфіцієнтів міжнейронного зв’язку. З виразу (9.15) видно, що нейронна мережа здатна враховувати нелінійні ефекти в інформаційних процесах, що підвищує ефективність обробки даних. Одна з головних проблем – настроювання коефіцієнтів зв’язку. Для цього можуть використовуватись процедури глобальної оптимізації, з урахуванням складного рельєфа цільової функції в багатовимірному параметричному пристрої коефіцієнтів зв’язку. В самій НМ динамічні процеси протікають порівняно швидко, а процеси оптимального настроювання параметрів є збіжними, але порівняно повільними. В системі можуть виникати численні рухи (“блуждания”), що приводить до перерегулювання. В зв’язку з цим спочатку проводять навчання нейромережового регулятора: - на моделі об’єкта; або: - в діючій системі при підключеному промисловому регуляторі (рис.9.5).
w1 w2 X UN - + Y T UR - + Рис.9.5. Схема системи з діючим регулятором
Оптимізатор 01 отримує сигнал m= UR – UN, за яким проводить настройку коефіцієнтів зв’язку нейромережового регулятора НР. Одночасно настроюється модель об’єкта в нейромережовому іденти-фікаторі НІ. Після закінчення процесу попереднього настроювання замість регулятора Р підключається нейромережевий регулятор НР. Може виникнути ситуація, коли в об’єкті відбуваються стрибко-подібні зміни структури, тоді необхідно передбачити реалізацію спеціальних режимів перенавчання нейронних мереж для уникнення значних похибок регулювання. Це може бути додаткова нейронна мережа для діагностики та відпрацювання аварійних ситуацій. В НМ із самоорганізацією проблема настройки параметрів мережі розв’язується по-іншому: замість процедури оптимізації використовуються статичні та динамічні моделі механізмів конкуренції між нейронами, а коефіцієнти міжнейронних зв’язків визначаються за значеннями поточного стану активності нейронів. Динамічна модель конкурентного типу описується системою нелінійних диференціальних рівнянь:
Zim – величина внутрішнього стану активності на вході m-го нейрона i-го шару; Xjk – вихідна величина k-го нейрона попереднього j-го шару; Yim – величина активності m-го нейрона i-го шару в процесі конкурентної взаємодії; Xim – вихідна величина m-го нейрону і-го шару; Wijmk, Cijmk – відповідно ваговий та нормований ваговий коефіцієнти зв’язку між m-ним та k-тим нейронами в і-му та j-му шарах; bik – ваговий коефіцієнт внутрішньошарового гальмування k-го нейрона i-го шару; Kim – кінетичний коефіцієнт швидкості зміни активності m-го нейрона і-го шару; g(×) – нелінійна функція обмеження. Процеси настроювання коефіцієнтів міжнейронного зв’язку в НМ із самоорганізацією можуть описуватись рівняннями, які визначають різні типи кривих росту рівня провідності синаптичних контактів між нейронами, які взаємодіють:
або:
Zim – величина внутрішнього стану активності m-го нейрона в i-му шарі; Xjk – вихідна величина k-го нейрона в j-му шарі. В результаті конкурентної взаємодії в процесі самоорганізації в НМ встановлюється певний розподіл активності нейронних елементів, який характеризує реакцію мережі на вхідне діяння. Динамічні рівняння, які описують стан НМ, можна розглядати як рівняння руху, які відповідають потенціальній функції, що визначає функціонал бажаної поведінки нейромережевої системи. Це може бути, наприклад, функціонал оптимальності управління або мінімума ентропії в деякій “синергетичній машині” для управління НМ в задачах розпізнавання образів. Приклад: для системи (рис.9.3), яка відпрацьовує заданий сигнал в умовах імпульсного діяння зовнішнього середовища, що приводить до збільшення інерційності об’єкта. НМ нейромережового регулятора складається з п’яти шарів, в кожному з яких 8,5, 5,5 і 1 нейрони відповідно. Нейроідентифікатор має три шари з числом нейронів 7,4,1. Початкова модель об’єкта – послідовно з’єднані інерційна та коли-вальна ланки:
На вхід подавався вхідний сигнал Т(t)=sin {[0,045+0,1sin (0,1t)]t} (9.20) В алгоритмах навчання НМ використані біологічні механізми типу флуктуація-мутація-відбір. Якщо відбуваються структурні зміні в об’єкті, то система з ПІД-регулятором стає нестійкою. Класичний регулятор задовільно працює в стаціонарних умовах, а нейромережовий – в умовах адаптації. Швидкість збіжності адаптивних процесів навчання залежить від: конфігурації мережі; алгоритмів настроювання; величини відхилень від умов нормальної роботи; Висновок: Нейрокомп’ютерні системи мають найширше застосу-вання при управлінні складними нелінійними об’єктами в умовах невизначеності і нестаціонарності. Апаратна реалізація нейрообчислювальних керуючих систем. Для роботи в реальному масштабі часу в умовах значних об’ємів оброблюваної інформації виникає необхідність виконання векторно-матричних операцій високої розмірності. Для цього в РЧ необхідно використовувати обчислювальні системи з паралельною обробкою даних, в першу чергу нейрокомп’ютери. Проблеми нейрокомп’ютерів почали обговорювати приблизно 50 років тому, але практична реалізація налічує буквально одиниці. В останній час знову виник підвищений попит на цю галузь, в 1998р. в ІПУ РАН відбулась IV конференція “Нейрокомп’ютери та їх застосування”, багато матеріалів в Internet. Нейрообчислювальний пристрій – система, орієнтована на реалі-зацію нейромережових алгоритмів. Головна особливість нейрокомп’ютерів – забезпечення високого паралелізму обчис-лень шляхом застосування спеціалізованого нейромережового логічного базиса або спеціальних архітектурних рішень. Реалізація нейромережових алгоритмів в цьому базисі дає можливість різко збільшити продуктивність (швидкодію) систем управління. Є багато визначень нейрокомп’ютера, але зручно розуміти під цим обчислювальну систему з MSIMD – архітектурою (обчислювальний пристрій з одним потоком команд та множинним потоком данних). Цифрові нейрокомп’ютери розробляються в таких напрямках: - програмна емуляція нейромережових алгоритмів на основі звичайних обчислювальних мереж та ППЗ моделювання НМ; - програмно-апаратна емуляція НМ на основі стандартних обчислювальних засобів з підключенням віртуального нейромережового блока, який виконує основні нейрооперації та відповідним ППЗ; - апаратна реалізація НМ. Найбільший ефект – при реалізації апаратними засобами, але це висока вартість і сьогодні існують одиничні спеціалізовані системи для конкретних задач. Наприклад, нейрокомп’ютер “Synaps 1” – представник нейрокомп’ютерів третього напрямку – має мультипроцесорну архітектуру, оригінальну будова підсистем пам’яті, а для виконання обчислювальних операцій застосовані сигнальні процесори матричного типу. Продуктивність (швидкодія) нейрокомп’ютера дякуючи цьому – декілька міліардів операц./сек. (множення та додавання). Програмне забезпечення – операційна система “ Synaps 1” з бібліотекою алгоритмів, а також ППЗ: - базова бібліотека НМ; - компілятор мови програмування нейроалгоритмів (nAPL); - набір бібліотечних функцій для С++ і т.д. Прикладні дослідження показали, що нейрокомп’ютери третього напрямку дозволяють підвищити продуктивність (швидкодію) звичайних обчислювальних систем мінімум на три порядки і моделю-вати НМ з міліонами з’єднань. Нейрокомп’ютер “ Synaps 1” дає можливість моделювати нейромережу з 64 млн з’єднань (синапсів) з використанням різноманітних активаційних функцій. Можна очікувати, що в подальшому з розвитком технології виробництва нейрочипів вартість обчислювальних систем буде зменшуватись, розширюватись область їх застосування. Найбільш поширений зараз нейрокомп’ютер “ Synaps 3”. Апаратна реалізація нейрообчислювального апаратно-програм-ного комплексу (АПК). АПК призначений для реалізації нейромережових алгоритмів. Для обробки сигналів АПК включає комплект датчиків і інтерфейсну плату (плати), що забезпечує спряження блоків датчиків з керуючою ЕОМ та первинну обробку інформації. В загальному випадку для апаратно-вимірювальних засобів застосо-вуються спеціалізований зовнішній контролер, з’єднаний з керуючою ЕОМ через інтерфейс IEEE-488, VXI bus, RS-485,-232 і т.д., а також віртуальний апаратний вимірювальний засіб, який може функціонувати лише тоді, коли приєднується до материнської плати ЕОМ через системну шину, наприклад ISA, EISA, PCI, Multibus, VMEbus і інше. Попередня обробка інформації та формування сигналів управління зараз може здійснюватись інтерфейсними платами на основі сигнальних процесорів. Основна умова ефективної роботи АПК – забезпечення РМЧ, коли система реагує на подію раніше, ніж наступить чергово подія. Нейрообчислювальний блок може реалізуватись на основі: - стандартного CISC мікропроцесора. Це фактично нейроемулятор і паралельні операції в РМУ не виконуються; - сигнальних процесорів або спеціалізованого нейроме-режового логічного базиса. В залежності від застосовуваних спеціалізованих засобів нейрообробки виділяють АПК: - з функціями нейроемулятора; - на базі каскадного з’єднання сигнальних процесорів; - нейрокомп’ютери (на основі нейромережового логічного базису).
9.4. Методи реінжинірінгу при створенні складних систем управління
Поиск по сайту: |

 i,j=1,...,s; k=1,...n
i,j=1,...,s; k=1,...n (9.15)
(9.15) m
m (9.16)
(9.16)
 ; i,j=1,...s; m,k=1,...n (9.17)
; i,j=1,...s; m,k=1,...n (9.17)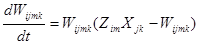 (9.18)
(9.18) (9.19)
(9.19)