 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Багатокритеріальні ЗПР
Приймемо: Х=(Х1,Х2...Хn) – n – вимірний вектор. Компоненти Хі зв’язані з конкретними фізичними та економічними показниками задачі, тобто обмежені:
Gj – векторна функція; bj – фіксована скалярна величина; Сj – деяка сукупність фіксованих величин (скаляр, вектор...). Ці умови визначають область допустимих стратегій Ωх, тобто з цієї області ОПР обирає стратегію в даній ситуації.
Ее= Ее (Ае,Х), е=1,к (8.8) Ае – сукупність фіксованих факторів. Частинним випадком відображення Х® Ее є функціональна залежність між критерієм Ее і стратегією Хj. Одночасне досягнення мети операції за всіма локальними крите-ріями при одній стратегії неможливо, тому рішення полягає в знаходженні компроміса в досягненні локальних цілей. Тоді виникає задача: - стратегія Хopt повинна належати множині Ωх її допустимих значень; - стратегія повинна бути найкращою стосовно прийнятого принципу компроміса з урахуванням вектора Λ важливості критеріїв Еopt=E(Xopt)=opt [E(x), Λ] (8.9) хÎΩх Оператор opt визначає принцип оптимальності, вибір найкращого рішення. Принцип оптимальності – математична модель принципа компроміса. Область Ωх можна розділити: - Ωхс – область згоди, коли рішення може бути покращено одночасно за всіма показниками (або принаймі без зниження рівня будь-якого з критеріїв); - Ωхк – область компромісів, в якій покращення якості рішення за одними локальними критерями приводить до погіршення якості рішення по іншим. Оптимальне рішення належить області компромісів Ωхк. Для вибору варіанта рішення необхідно розкрити оператор opt, тобто знайти схему компроміса, що здійснює ОПР суб’єктивно. При аналізі схеми компромісу приймається, що локальні критерії нормалізовані (мають однакову розмірність або є безрозмірними) та мають однакову важливість. Використовуючи область допустимих критеріїв, можна записати: Еopt=E(Xopt)=opt[E(X), Ù]=opt[E, Ù] хÎΩх ЕÎΩЕк (8.10) Схеми компромісу: (принципи) рівномірність; справедливої поступки; виділення одного оптимізуємого критерія; послідовних поступок і інш. 1.Для забезпечення одночасно екстремума функцій f1(x), f2(x)...fn(x) використовується лінійна згортка:
Ci – додатні числа, нормовані наприклад так: При такому способі згортки вводиться відношення еквівалентності різних критеріїв, а величини Ci показують, наскільки змінюється функція F(х) при зміні критерія fі(x) на одиницю: Значення Ci – результат експертизи, вони дають уявлення оперуючої сторони про зміст компромісу (вимушеного). Зміст компроміса – ранжування цілей, яке разом з призначенням вагових коефіцієнтів є додатковою гіпотезою для зведення багатокритеріальної задачі до однокритеріальної.
Цільову функцію подають у виді
і шукають вектор х, який забезпечує максимальне значення F(х). Наприклад:
f2(x)=x2 f2*(x)=2 f1(x)=6x f3*(x)=8 1. х=1 2. х=2 В чому смисл? При даному значенні вектора Х величина F(x) дає значення найгіршого показника fi(x). Значить умова F(x) ®max означає вибір таких конструктивних параметрів х, які максимізують відношення і-го реально досягнутого значення критерія до його контрольного значення. Якщо значення fi* жорстко не задаються, то вони можуть визначатись в результаті експертного опитування. 3. Виділення одного критерія. Якщо є контрольні показники fi* відносно яких критерії fi(x) повинні задовольняти умовам:
то серед них можна визначити основний f1(x) ®max 4. fі(x) ®max; i=1,n, а в і-й задачі знайдемо вектор х=хі, який доставляє max критерію fі(x):
Сукупність скалярних величин
визначає в просторі критеріїв деяку відстань від точки, яка відповідає даному вектору х, до точки “абсолютного максимума”. В частинному випадку, коли R – одинична матриця
- евклідова відстань від точки (f1(x1), f2(x2)... fn(xn)) до точки ( В цьому випадку мінімізація h як нового критерія дає корисну інформацію – показує граничні можливості досягнення “абсолютного максимума”. 5. Компроміси Парето Смисл згортки критеріїв – одна задача замінюється іншою, але можна підійти до аналіза багатокритеріальних задач з інших позицій: спробувати скоротити множину початкових варіантів, тобто виключити з аналізу ті варіанти рішень, які будуть наперед незадовільними. Один з шляхів – економіст В.Парето (1904, Італія).
fі( причому хоча б одна нерівність – строга. Тоді зрозуміло, що вибір Допустимо, що цілі об’єкта визначаються двома однозначними функціями f1(x)®max, f2(x)®max (рис.8.2)
Рис.8.2. Площина критеріїв
Тоді кожному допустимому значенню змінної х відповідає одна точка на площині, (f1, f2), а рівності f1= f1(х), f2= f2(х) визначають параметричне завдання деякої кривої abcd на цій площині. Але до множини Парето можна віднести далеко не всю криву: так дільниця bc, очевидно, не належить до множини Парето, бо з ростом f1 відбувається зростання і f2. Це значить, що на цій дільниці зміні х відповідає одночасне зростання обох цільових функцій, і ці варіанти треба виключити з розгляду. Так само виключається дільниця а/b, бо для кожної її точки e можна знайти на cd точку, в якій значення обох функцій f1 і f2 більші, чим в точці e. Таким чином, на належність до множини Парето можуть претендувати лише дільниці аа/ і cd , причому точка а/ повинна виключатись. Принцип Парето не виділяє єдиного рішення, він лише звужує кількість альтернатив. Прийняття рішень в умовах невизначеності. Задача прийняття рішень (ЗПР) в умовах невизначеності – вибір оптимальної стратегії в операції, результат якої крім стратегій оперуючої сторони і ряду фіксованих факторів (детермінованих, стохастичних або і тих, і інших) залежить від невизначених факторів, невідомих в момент прийняття рішень, не залежних від оперуючої сторони. Тому кожній стратегії оперуючої сторони відповідає не єдиний (як в детермінованому випадку), а множина можливих результатів. Необхідно розрізняти стохастичні і невизначені фактори. Щодо стохастичних факторів, то для них існує достатньо повна стохастична інформація, а невизначені фактори проявляються внаслідок недостатньої інформації щодо “природи” операції: невідомі характеристики процесів та властивості об’єктів, зовнішні умови. Можна виділити дві групи факторів, які викликають невизначеності нестохастичної природи: - стратегічні невизначеності, коли в операції приймають участь кілька оперуючих сторін, які мають різні цілі, і кожна сторона приймає рішення в умовах, коли дії інших учасників невідомі; - концептуальні невизначеності – невизначені фактори для особ-ливо складних рішень з довгостроковими наслідками, нечіткими уявленнями про власні цілі інших учасників. Тут часто виникає конфліктна ситуація, для аналізу якої і прийняття рішення в умовах активної дії кількох учасників використовуються теорія ігор та мінімакса (максиміна). З конфліктними ЗПР пов’язані передумови: - кожному учаснику відомі цілі і стратегії інших; - кожен учасник є розумним та активним, тому визначальними в його поведінці вважається прагнення максимального досягнення власних цілей. Це спрощує підхід до прийняття рішень, на цьому засновані теорія ігор і теорія мінімакса. З урахуванням “природи” ситуації ЗПР ускладнюється: їй не можна приписати свідомо поставлених цілей, але людина поступово вивчає закони природи і знижує, зменшує невизначеності.
- результат операції: sj, j=1,m приймають: А – виграш ОПР, А – втрати. Тоді в табличному вигляді або матриці втрат (виграшів) задається:
aij=A(xi, sj) – виграш для рішення xi при sj.
r(x/)=РА/ (x/, sj) – число, ризик, пов’язаний з стратегією x/. Тоді: найкращою є стратегія (якщо вона існує) Х*ÎХ, яка мінімізує ризик на множині Х:
xi ÎХ Критерії оптимальності вибору рішень ОПР за умови відсутності апріорної інформації щодо результатів операції sj. Критерій Лапласа. Приймається, що ймовірності результатів sj рівні. Тоді для кожного рядка матриці виграшів A=|aij| підраховується середнє значення оцінок, а оптимальна стратегія – максимальне значення цього середнього:
Критерій Вальда. Оптимальною вважається стратегія, коли міні-мальний виграш є максимальним, тобто гарантується виграш, не менший, ніж максимін:
Цей критерій орієнтує ОПР на найгірші умови та рекомендує обирати стратегію, для якої в гірших умовах виграш максимальний (принцип – “завжди необхідно розраховувати на гірше”). Це – критерій крайнього песимізму. Критерій Севіджа. Можна в кожному стовбці матриці виграшів A=|aij| обрати max aij і скласти нову матрицю: 1£ і £ n rij=max aij - aij (8.18) 1£ і £ n Матриця ризиків R=| rij | дає можливість обрати стратегію, за якою величина ризику приймає найменше значення в самій несприятливій ситуації:
Сутність критерія – за будь-яких умов уникнути великого ризику при прийнятті рішень. Це теж критерій крайнього песимізму, але гіршим тут є не мінімальний виграш, а максимальний ризик – максимальна втрата виграшу в порівнянні з тим, що можна було досягнути за даних умов. Критерій Гурвиця. Між крайнім песимізмом (розрахунок на гірше) та легковажним оптимізмом (розрахунок на краще) при виборі стратегії в умовах невизначеності критерій Гурвиця рекомендує розраховувати на деякий середній результат:
a - коефіцієнт оптимізму, 0 £ a £ 1. При a=1 критерій Гурвиця перетворюється в критерій крайнього песимізму Вальда, при a=0 – критерій крайнього оптимізма, коли рекомендується обирати стратегію, за якої в найкращих умовах виграш максимальний; при 0 < a < 1 – середня оцінка між крайнім песимізмом та крайнім оптимізмом, a - міра песимізму ОПР. Чим більш небезпечна ситуація, тим більше намагаються “підстрахуватись”, a®1. Критерій Байєса. В цьому випадку на множині всіх ситуацій вва-жається відомим апріорне розподілення ймовірностей Р(sj). Цей критерій мінімізує середні втрати, тобто ризик тут – математичне сподівання:
Найкраща стратегія мінімізує ризик:
Поиск по сайту: |
 В загальному випадку стратегія оперуючої сторони Хі, i=1,n може бути скаляром, вектором, матрицею або ще більш складним утворенням.
В загальному випадку стратегія оперуючої сторони Хі, i=1,n може бути скаляром, вектором, матрицею або ще більш складним утворенням. Gj= Gj(Сj,Х) ³ bj, j=1,m (8.7)
Gj= Gj(Сj,Х) ³ bj, j=1,m (8.7)

 Ефективність дій оперуючої сторони оцінюється сукупність локальних критеріїв Е1, Е2...Ек, які мають коефіцієнти відносної важливості l1, l2,... lк. Тоді є два вектори: Ù=(le), e=1,к і Е=(Еe), e=1,к. Кожний критерій характеризує локальну мету операції і зв’язаний із стратегією відображенням.
Ефективність дій оперуючої сторони оцінюється сукупність локальних критеріїв Е1, Е2...Ек, які мають коефіцієнти відносної важливості l1, l2,... lк. Тоді є два вектори: Ù=(le), e=1,к і Е=(Еe), e=1,к. Кожний критерій характеризує локальну мету операції і зв’язаний із стратегією відображенням.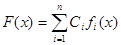 (8.11)
(8.11) .
. .
. (8.12)
(8.12) f1(x)=2x f1*(x)=4
f1(x)=2x f1*(x)=4 ;
;  ;
; 
 ;
;  ;
; 
 fi(x) ³ f*i , i=1,n,
fi(x) ³ f*i , i=1,n, fі(xі)=
fі(xі)=  , i=1,n
, i=1,n ,
,  ,...
,... 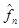 ) є недосяжною в просторі критеріїв. Вводиться додатньо визначена матриця R=(rij). Тоді скалярна величина:
) є недосяжною в просторі критеріїв. Вводиться додатньо визначена матриця R=(rij). Тоді скалярна величина: (8.13)
(8.13) (8.14)
(8.14) такий, що для всіх критеріїв fі(x) мають місце нерівності:
такий, що для всіх критеріїв fі(x) мають місце нерівності: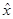 ) ³ fі(х*), i=1,n,
) ³ fі(х*), i=1,n, кращий х1* і можна одразу всі вектори х*, які задовольняють умові, виключити з розгляду. Має смисл співставляти і аналізувати лише ті вектори х*, для яких не існує
кращий х1* і можна одразу всі вектори х*, які задовольняють умові, виключити з розгляду. Має смисл співставляти і аналізувати лише ті вектори х*, для яких не існує  ) ³ fі(х*) для будь-якого і випливає fі(
) ³ fі(х*) для будь-якого і випливає fі( 
 f2 a c
f2 a c

 a/ q
a/ q е
е b d
b d f1
f1 - ОПР може обрати один з n можливих варіантів рішень хі, і=1,n;
- ОПР може обрати один з n можливих варіантів рішень хі, і=1,n;
 A=|aij|, A=|aij|, (8.15)
A=|aij|, A=|aij|, (8.15) r(x*)=min r(xi), і=1,n (8.16)
r(x*)=min r(xi), і=1,n (8.16) (8.17)
(8.17)
 (8.19)
(8.19)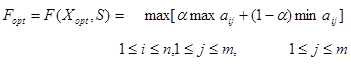 (8.20)
(8.20) (8.21)
(8.21) (8.22)
(8.22)