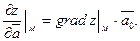|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ №7⇐ ПредыдущаяСтр 20 из 20
Література: [1], т. І, с.200-217, 239-260, [2], с.373-431, [3], с. 217-262, 341-377. Правило, за яким кожній парі чисел (x;y)Î D ставиться у відповідність єдине число z, називається функцією двох змінних, що визначена на множині D. Позначення: z= f (x,y). Частинною похідною за змінною x від функції z=f(x,y) називається функція, яка одержана при диференціюванні f(x,y) за змінною x у припущенні, що y=const:
Повним диференціалом функції двох змінних z=f (x;y)називається вираз dz= який є головною частиною повного приросту функції, лінійного відносно dx, dy. Градієнт функції z в точці M(x0;y0):
Похідна функції z в точці М за напрямом вектора
Перед виконанням завдання № 7 рекомендується опрацювати приклади 7.21-7-26 глави ІІ. РЕКОМЕНДОВАНА ЛІТЕРАТУРА
Основна література 1. Барковський В.В., Барковська Н.В. Математика для економістів. Вища математика. - К.: Національна академія управління, 1999 р. – 399 с. 2. Валєєв К.Г., Джалладова І.А. Вища математика: Навч. посібник: У 2-х ч. – Ч.1. – К.: КНЕУ, 2001. – 546 с. 3. Васильченко І.П. Вища математика для економістів. - Видавництво "Знання", 2007 - 456c.
Додаткова література 1. Бобик О.І., Гладунський В.Н., Засадна Х.О. Математика для економістів: Вища математика. Навч. посібник у 3-х ч. – Ч.1. – Львів: Вид-во УБС НБУ, 2007. – Ч.2. – Львів: Вид-во УБС НБУ, 2008. 2. Бугір М.К. Математика для економістів. Навч. посібник.– К.: Альма Матер, 2003. 3. Бондарев Б.В., Шурко И.Л. Финансовая математика. Учебное пособие. – Донецк: Кассіопея, 1998. 4. Бакаев Л.О. Кількісні методи в управлінні інвестиціями: Навч. Посібник. – к,: КНЕУ, 2000. 5. Башарин Г.П. Начала фининсовой математики. М.: ИНФРОА – М, 1997 6. Вітлінський В.В. Моделювання економіки: Навч. посібник. – К.: КНЕУ, 2003. 7. Гладунський В.Н. Вища математика й елементи логіки: означення, формули, приклади. Навч. посібник. – Львів: Афіша, 2005. 8. Григулецький В.Г., Ященко З.В. Высшая математика для экономистов. – Фенікс, 2004. 9. Єлейко Я.І., Кандибко О.М., Лапішко М.Л., Смовженко Т.С. Основи фінансового аналізу. – Львів: ЛБІ НБУ, 2000. 10. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник; МГУ им. М.В.Ломоносова. – 4-е изд., стереотип. – М.: Изд-во «Дело и сервис», 2004. 11. Кленко В.Ю., Голець В.Л. Вища математика в прикладах і задачах. Видання друге перероблене і доповнене. Навчальний посібник. – К.: УНЛ, 2006. 12. Кремер Н.Ш. и др. Высшая математика для экономистов — М.: Банки и биржи, ЮНИТИ, 1997. 13. Козицький В.А., Лавренюк С.П., Оліскевич М.О. Основи математичної економіки. Теорія споживання:Навч. посібник. – Львів: Видавництво «Піраміда». 2004. 14. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учеб. – 2-е изд., испр. – М.: Дело, 2001. – 688с. 15. Козицький В.А., Лавренюк С.П., Оліскевич М.О. Основи математичної економіки. Теорія фірми:Навч. посібник. – Львів: Видавництво «Піраміда». 2004. 16. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов. Уч. пособие для подготовки бакалавров экономического профиля. – Донецк, 1998. 17. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: Учебник: В 2-х ч. Ч.1. – М.: Финансы и статистика, 2001. – 224 с. 18. Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збірник задач та вправ. – Х.: Рубікон, 1999. – 320 с. 19. Тріщ Б.М. Основи вищої математики. – Львів: Вид. центр ЛНУ ім. Ів. Франка, 2006. 20. Четыркин Е.М. Финансовая математика: Учебник. – 5-е изд., испр. – М.: Дело 2005. ЗМІСТ
Поиск по сайту: |
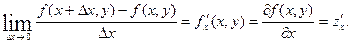
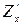 dx+
dx+  dy,
dy,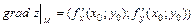
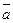 :
: