 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рекомендації до розв’язання типових прикладів розділу 5
5.1.Знайти довжину вектора Розв¢язання. 1) Якщо вектор
2) Якщо
3)Якщо
5.2.Знайти орт вектора Розв’язання.
Тоді Відповідь: 5.3.У трикутнику з вершинами А(2;-1;3), В(-2;2;5), С(1;2;3) знайти кут при вершині А.
cosj= j » arccos 0,763 »40°18¢. 5.4.Знайти точку D так, щоб чотирикутник АВСD був паралелограмом, якщо А(-2; 0), В(1; -3), С(2; 5). Розв¢язання.
Якщо АВСD- паралелограм, то
З умови рівності координат маємо: 2 –х = 3, 5-у =-3, звідси х = -1, у = 8. Отже, одержали координати точки D (-1; 8). 5.5.Знайти точку С на осі Оy так, щоб кут АВС був прямим, якщо задані точки А(6; 4), В(-2; 5). Розв¢язання. Введемо (0; у) –координати точки С. Необхідною та недостатньою умовою ортогональності векторів
Тоді маємо 8×2 -1×(у-5) =0, 16 – у + 5 =0, у = 21. Отже, маємо С(0; 21).
5.6.Розкласти вектор
Розв¢язання. Розкласти вектор
У результаті приходимо до системи рівнянь
вирішуючи яку, знаходимо:
Звідси
5.7.Скласти рівняння прямої, що проходить через точки М(-1; 3) та N(2; 5) Розв’язання. Скористаємося рівнянням прямої на площині, що проходить через точки М1(х1; у1)та М2(х2; у2):
Підставляючи в це рівняння наші дані, одержуємо
Рівняння має вигляд 2х –3у +11= 0. Корисно перевірити, що рівняння складено вірно. Для цього достатньо показати, що координати точок М та N задовольняють рівнянню прямої. Дійсно, рівності 2(-1)-3·3+11= 0, 2·2- 3·5 +11=0 виконуються тотожно.
5.8.Дані вершини трикутника: M(0;1); N(6;5) та С(12;-1). Скласти рівняння висоти трикутника, проведеної з вершини С. Розв’язання.
Скористаємося рівнянням прямої на площині, яка проходить через точку C(x0; y0)та має вектор нормалі A(х-х0) + В(у-у0) =0. Зі схематичного рисунка видно, що в якості вектора нормалі прямої СК можна взяти вектор 6(x-12) + 4(у+1) =0, звідки одержуємо 3х +2у –34 =0.
5.9.Скласти рівняння прямої, що проходить через точку М(-2; -5) і паралельно прямій 3х +4у +2 =0.
З схематичного рисунка бачимо, що вектор нормалі 3(х+2) + 4(у+5) =0, звідки 3х + 4у +26 =0.
5.10.Дані вершини трикутника А(-2; -3), В(5; 4) та С(-1; 2). Скласти рівняння медіани АМ. Розв’язання. Точка М –середина сторони ВС, тому
Використовуючи рівняння прямої, що проходить через точки А і М, знаходимо рівняння медіани АМ: 5.11.Провести серединний перпендикуляр відрізка АВ, де А(0; -2), В(4; 0). Розв’язання.
Маємо С(2; -1). Розглядаючи
5.12.Дані рівняння сторін трикутника: х + 3у –7= 0 (АВ), 4х –у- 2= 0 (ВС),6х +8у –35= 0 (АС). Знайти довжину висоти, проведеної з вершини В.
Визначимо координати точки В. Розв’язуючи систему рівнянь х + 3у –7= 0 та 4х –у- 2= 0, одержимо х=1,у= 2, тобто В(1;2). Скористаємося формулою для обчислення відстані від точки М0( х0;у0)до прямої Ах +Ву + С =0:
Знаходимо довжину висоти ВВ1 як відстань від точки В до прямої АС:
5.13.Знайти проекцію точки Р(4;9)на пряму, що проходить через точки А(3; 1) та В(5; 4). Розв’язання. Проекція точки на пряму- це основа перпендикуляра, опущеного з точки на пряму. Для її одержання достатньо розв”язати сумісно рівняння прямої АВ і прямої, що проходить через точку Р перпендикулярно АВ. Рівняння АВ запишемо, скориставшись рівнянням
Тоді
Поиск по сайту: |
 , якщо відомі координати точок А(2; -1), В(-3; 0), С(5; -2).
, якщо відомі координати точок А(2; -1), В(-3; 0), С(5; -2). має своїм початком точку А(х1; у1; z1), а кінцем точку В(х2; y2; z2), то координати вектора
має своїм початком точку А(х1; у1; z1), а кінцем точку В(х2; y2; z2), то координати вектора 
 то
то
 то довжина
то довжина  . Тоді
. Тоді 


 ,
,
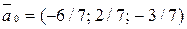
 Розв¢язання.
Розв¢язання. тоді
тоді

 а два вектори рівні, якщо рівні відповідні координати. Позначимо через х,у невідомі координати точки D. Тоді
а два вектори рівні, якщо рівні відповідні координати. Позначимо через х,у невідомі координати точки D. Тоді
 є рівність нулю їх скалярного добутку:
є рівність нулю їх скалярного добутку:  Скористуємося формулою для обчислення скалярного добутку:
Скористуємося формулою для обчислення скалярного добутку: де
де 
 по векторах
по векторах 
 та
та
 по векторах
по векторах  означає представити його у вигляді лінійної комбінації
означає представити його у вигляді лінійної комбінації - поки ще невідомі числа. Переходячи до координат, одержимо
- поки ще невідомі числа. Переходячи до координат, одержимо
 ,
,

 .
. або
або  .
.
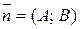 :
: . Тоді маємо:
. Тоді маємо: Розв’язання.
Розв’язання. даної прямої є і вектором нормалі шуканої прямої. Тоді, застосувавши рівняння з попередньої задачі, маємо:
даної прямої є і вектором нормалі шуканої прямої. Тоді, застосувавши рівняння з попередньої задачі, маємо: .
. звідки 3х-2у=0.
звідки 3х-2у=0.
 як вектор нормалі шуканої прямої, маємо: 4(х-2) +2(у+1) =0, звідки 2х + у –2 =0.
як вектор нормалі шуканої прямої, маємо: 4(х-2) +2(у+1) =0, звідки 2х + у –2 =0. Розв’язання.
Розв’язання.

 де
де  та
та  - відомі точки прямої.
- відомі точки прямої. або
або  .
.