 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачі, рекомендовані до розв’язання на практичних заняттях з розділу 5
1. За даними векторами 2. Маємо: 3. Маємо: | 4. Вектори a і b взаємно перпендикулярні, причому | 5. Вектори 6. Вектори 7. Якій умові повинні задовольняти вектори 8. Якій умові повинні задовольняти вектори 9. За даними векторами
10. Точка О є центром ваги трикутника АВС. Довести, що 11. Перевірити колінеарність векторів 12. Визначити, при яких значеннях a,b вектори 13. Перевірити та впевнитись, що чотири точки А(3; -1; 2), 14. Маємо точки А(-1; 5; -10), В(5; -7; 8), С(2; 2; -7) та D(5; -4;2). Перевірити і впевнитись, що вектори 15. Маємо дві вершини А(2; -3;-5), В(-1;3; 2) паралелограма АВСD і точку перетину його діагоналей Е(4; -1; 7).Визначити дві інші вершини цього паралелограма. 16. Маємо три вершини А(3; -4; 7), В(-5; 3; -2) та С(-4; 2; -3) паралелограма АВСD. Знайти його четверту вершину D, протилежну В. 17. Знайти орт вектора: а) 18. На площині є три вектори 19. Маємо три вектори 20. Маємо три вектори 21. Маємо чотири вектори 22. Вектори
24. Маємо вектори 25. Маємо точки А(-1; 3; -7), В(2; -1; 5) та С(0; 1; -5). Обчислити: 26. Маємо вершини чотирикутника А(1; -2; 2), В(1; 4; 0), С(-4; 1; 1) та D(-5; -5; 3). Довести, що його діагоналі АС та ВD взаємно перпендикулярні. 27. Визначити, при 28. Маємо вершини трикутника А(-1; -2; 4), В( -4; -2; 0) та С(3; -2; 1). Визначити його внутрішній кут при вершині В. 29. Обчисливши внутрішні кути трикутника А(1; 2; 1), В(3; -1; 7), С(7; 4; -2), впевніться, що цей трикутник рівнобедрений. 30. Вектор 31. Знайти вектор 32. Маємо два вектори: 33. Маємо пряму 2х+3у+4=0. Скласти рівняння прямої, що проходить через точку М0(2;1): 1) паралельно даній прямій; 2) перпендикулярно до даної прямої. 34. Маємо рівняння двох сторін трикутника 2х-3у+5=0, 3х+2у-7=0 і одна з його вершин А(2; -3). Скласти рівняння двох інших сторін цього прямокутника. 35. Знайти точку Q, симетричну точці P(-5; 13) відносно прямої 2х-3у-3=0. 36. Маємо середини сторін трикутника М1(2; 1), М2(5; 3) та М3(3; -4). Скласти рівняння його сторін. 37. Скласти рівняння прямої, якщо точка Р(2; 3) є основою перпендикуляра, опущеного з початку координат на цю пряму. 38. Сторони трикутника задані рівняннями 4х-у-7 =0, х+3у-31=0, х+5у-7=0. Визначити точку перетину його висот. 39. Маємо вершини трикутника А(1; -1), В(-2; 1) та С(3; 5). Скласти рівняння перпендикуляра, опущеного з вершини А на медіану, проведену з вершини В. 40. Знайти проекцію точки Р(-8; 12) на пряму, що проходить через точки А(2; -3) та В(-5; 1). 41. Визначити кут j між двома прямими: 1) 5х-у+7=0, 3х+2у=0; 2) 3х-2у+7=0, 2х+3у-3=0. 42. Точка А(-4; 5) є вершиною квадрата, діагональ якого лежить на прямій 7х-у+8=0. Скласти рівняння сторін і другої діагоналі цього квадрата. 43. Маємо дві протилежні вершини квадрата А(-1; 3) та С(6; 2). Скласти рівняння його сторін. 44. Встановити, які з вказаних пар прямих перпендикулярні: 1)3х-у+5=0, 2) 3х-4у+1=0, х+3у-1=0; 4х-3у+7=0. 45. Визначити кут j , утворений двома прямими: 1)3х –у +5 =0, 2х +у –7 =0;
46. Маємо дві вершини трикутника М1(-10; 2) та М2(6; 4); його висоти перетинаються в точці N(5; 2). Визначити координати третьої вершини М3. 47. Маємо дві вершини А(3; -1) та В(5; 7) трикутника АВС і точку N(4; -1) перетину його висот. Скласти рівняння сторін цього трикутника. 48. Знайти радіус і координати центра кола, заданого рівнянням х2+у2+8у-10х+37=0. 49. Встановити, яка лінія визначена рівнянням 4х2+9у2-8х+36у+4=0, і побудувати цю лінію. 50. Маємо дві точки М1(3; -1; 2) та М2(4; -2; -1).Скласти рівняння площини, що проходить через точку М1 перпендикулярно вектору 51. Скласти рівняння площини, що проходить через три точки: М1(3; -1; 2), М2(4; -1; -1) та М3(2; 0; 2), знайти відстань від точки Р(-2; 1; 0) до цієї площини. 52. Визначити, при яких значеннях l та m вказані пари рівнянь будуть визначати паралельні площини: 1) 2x +Ly +3z -5=0, mx- 6y -6z + 2=0; 2) 3x –y +Lz -9=0, 2x+ my +2z –3 =0. 53. Визначити, при яких значеннях L вказані пари рівнянь будуть визначати перпендикулярні площини: 1) 3x -5y +Lz -3=0, x+ 3y +2z + 5=0; 2) 5x –y -3z -3=0, 2x+ Ly -3z + 1 =0; 3) 7x -2y -z =0, Lх+ y -z – 1=0. 54. Визначити двогранні кути, утворені перетином таких пар площин:
55. Скласти рівняння площини, що проходить через початок координат паралельно площині 5х –3у +2z –3 =0. 56. Скласти рівняння площини, що проходить: 1) через точку М1(3; -2; -7) паралельно площині 2х –3z +5 =0; 2) через О(0,0,0); 3) через М1|| XOY; 4) через М1 і вісь OZ. 57. Встановити, що три площини x -2y +z –7 =0, 2x +y –z +2 =0, x -3y +2z –11 =0 мають одну загальну точку, і обчислити її координати. 58. Обчислити відстань d від точки Р(-1; 1; -2) до площини, що проходить через точки М1(1; -1; 1), М2(-2; 1; 3) та М3(4; -5; -2). 59. У кожному з наступних випадків обчислити відстань між паралельними площинами: 1) x -2y -2z –12 =0, 2) 2x –3y +6z –14 =0, x –2y –2z –6 =0; 4x –6y +12z +21 =0. 60. Скласти канонічні і параметричні рівняння прямої, що проходить через точку М1(2; 0; -3) паралельно: 1) вектору 2) прямій 3) осі Оy. 61. Скласти канонічні та параметричні рівняння прямої, що проходить через дві точки: 1) (1; -2; 1), (3; 1; -1); 2) (3; -1; 0), (1; 0; -3). 62. Скласти параметричні рівняння прямої, що проходить через точку М1(1; -1; -3) паралельно: 1) вектору 2) прямій 3) прямій x =3t –1, y =-2t +3, z =5t +2. 63. Знайти гострий кут між прямими: 64. Довести, що пряма x= 3t –2, y= -4t +1, z= 4t –5 паралельна площині 4x –3y –6z –5 =0. 65. Знайти точку перетину прямої і площини:
66. Скласти рівняння прямої, що проходить через точку М0(2; -3; -5) перпендикулярно до площини 6x -3y -5z +2 =0. 67. Скласти рівняння площини, що проходить через точку М0(1; -1; -1) перпендикулярно прямій 68. При якому значенні m пряма 69. При яких значеннях А і В площина Ax + By +3z –5 =0 перпендикулярна прямій x= 3 +2t, y= 5 –3t, z= -2 –2t ? 70. При яких значеннях L і C пряма 71. Знайти проекцію точки Р(2; -1; 3) на пряму x= 3t, y =5t-7, z =2t +2. 72. Знайти проекцію точки Р(5;2; -1) на площину 2x –y +3z +23 =0. 73. Витрати виробництва на 10 одиниць деякого товару складають 1000 грн.од., на 50 одиниць товару – 2000 гр.од. Визначити витрати виробництва на 30 одиниць товару за умови, що витрати залежать від об’єму продукції лінійно. 74. Скласти рівняння прямої, яке відображає зміну врожайності 1 га протягом сімнадцяти років, якщо в перший рік з 1 га було зібрано 9,1 ц зернових культур, а в останній рік – 21 ц. 75. Два однотипних підприємства А і В виробляють продукцію з однаковою оптовою відпускною ціною m за один вирыб. Але автопарк, який обслуговує підприємство А, оснащений більш новими і більш потужнішими грузовими автомобілями. У результаті цього транспортні витрати на перевозку одного виробу складають на 1 км: для підприємства А 10 грн.од., а для підприємства В – 20 грн.од. Відстань між підприємствами 300 км. Як територіально має бути розділений ринок збуту між двома підприємствами для того, щоб витрати користувача при навантажуванні виробів і їх транспортуванні були мінімальними. 76. Дві фірми реалізують продукцію з однією і тією же оптовою відпускною ціною p (гр. од.) за один комп'ютер. Транспортні витрати на перевезення одного комп'ютера складають для першої фірми ‑ 15 гр.од., а для іншої ‑ 30 гр. од. Відстань між фірмами 450 км. Дослідити, як територіально повинний бути розділений ринок збуту між двома фірмами для того, щоб витрати споживача при навантаженні виробів і їхньому транспортуванню були мінімальними? 77. Транспорті витрати на транспортування продукції від одного заводу в три рази дешевше, ніж від іншого. Відстань між двома заводами, що виробляють однакову продукцію, 200 км. Побудувати графік кривої і визначити всі райони, в яких однаково вигідно одержувати продукцію обох заводів.
Розділ 6. ЕЛЕМЕНТИ ТЕОРІЇ ГРАНИЦЬ ФУНКЦІЇ ОДНІЄЇ І БАГАТЬОХ ЗМІННИХ
Основні питання, що виносяться на практичні заняття за розділом 6: 1. Обчислення границь. Розкриття невизначеностей вигляду 2. Обчислення границь за допомогою першої особливої границі. 3. Обчислення границь за допомогою другої особливої границі. 4. Дослідження функції на неперервність. Знаходження точок розриву та їх класифікація.
Поиск по сайту: |
 і
і  побудувати кожен з наступних векторів: 1)
побудувати кожен з наступних векторів: 1)  Обчислити |
Обчислити | 
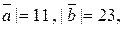 та |
та | 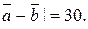 Визначити |
Визначити | 
 | та |
| та | 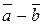 |.
|.
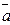 і
і 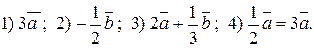

 {-6; 3; -9}. Визначити, який з них довше і у скільки разів, як вони направлені - в один бік чи в протилежні сторони.
{-6; 3; -9}. Визначити, який з них довше і у скільки разів, як вони направлені - в один бік чи в протилежні сторони. та
та  колінеарні; встановити який з них довше і у скільки разів, як вони направлені - в один бік чи в протилежні сторони.
колінеарні; встановити який з них довше і у скільки разів, як вони направлені - в один бік чи в протилежні сторони. =(7; -4). Визначити розклад кожного з цих трьох векторів, приймаючи в якості базису два інших.
=(7; -4). Визначити розклад кожного з цих трьох векторів, приймаючи в якості базису два інших. за базисом
за базисом 
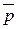 =(3; -2; 1),
=(3; -2; 1),  =(-1; 1; -2) та
=(-1; 1; -2) та  =(2; 1; -3). Знайти розклад вектора
=(2; 1; -3). Знайти розклад вектора  = (11; -6; 5) за базисом
= (11; -6; 5) за базисом 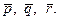

 (3; 7; -7). Визначити розклад кожного з цих чотирьох векторів, приймаючи в якості базису останні три.
(3; 7; -7). Визначити розклад кожного з цих чотирьох векторів, приймаючи в якості базису останні три. ; знаючи, що |
; знаючи, що | 

 ; знаючи, що |
; знаючи, що |  ,|
,|  та
та 
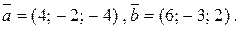 Обчислити:
Обчислити: 

 взаємно перпендикулярні.
взаємно перпендикулярні.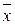 , колінеарний вектору
, колінеарний вектору  |=50, знайти його координати.
|=50, знайти його координати.


 .
.




 .
. паралельна площині x –3y +6z +7 =0 ?
паралельна площині x –3y +6z +7 =0 ? перпендикулярна площині 3x –2y +Cz +1 =0 ?
перпендикулярна площині 3x –2y +Cz +1 =0 ?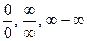 .
.