 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рекомендації до розв’язання типових прикладів розділу 3
3.1. Розв’язати систему лінійних рівнянь за правилом Крамера.
Складемо матрицю системи рівнянь, обчислимо визначник системи та додаткові визначники:
Відповідь: х = 2 ; y = -2 ; z = 1. 3.2. Розв’язати систему лінійних рівнянь, подану в прикладі 1, за допомогою оберненої матриці. При розв’язуванні попереднього прикладу ми склали матрицю системи А і обчислили визначник
Знайдемо обернену матрицю
Тоді
Відповідь:
3.3. Розв’язати систему лінійних рівнянь, подану у прикладі 1, методом Гаусса:
Виключаємо невідоме х із другого і третього рівнянь
y= – 2 3 z = 5 + y; 3z = 3; z = 1 x = – 3 – 2y + z; x = – 3 – 2 (–2) + 1 = 2 Таким чином, x = 2, y = -2, z = 1. Відповідь: x = 2, y = -2, z = 1. 3.4. Розв’язати систему лінійних рівнянь методом Гаусса:
Виключаємо невідоме х1 із другого і третього рівнянь
Розглянувши третє рівняння, робимо висновок, що система рівнянь не має розв’язків (система лінійних рівнянь несумісна). 3.5. Розв’язати систему рівнянь методом Гаусса
Ділимо перше рівняння на 3 і виключаємо невідоме х1 з другого і третього рівнянь
Ділимо друге рівняння на
Останнє рівняння є тотожністю, його можна відкинути. Одержимо систему
Покладаємо х3 = t. Тоді з другого рівняння
і з першого рівняння
Таким чином, загальний розв’язок системи рівнянь має вигляд
де t може приймати будь-які числові значення. Відповідь: 3.6. Розв’язати систему лінійних рівнянь, наведену у прикладі 1, методом Жордана – Гаусса.
Пояснення до розрахункової таблиці Обираємо розв’язувальний елемент а31 (розв’язувальний рядок – третій). Елементи стовпця контрольної суми ( S ) обчислюємо як суму елементів відповідного рядка (наприклад, для першого рядка: 1 + 2 + (-1) + (-3) = -1). Шляхом елементарних перетворень (множенням елементів розв’язувального рядка на (-1) і додаванням до відповідних елементів першого рядка та множенням елементів розв’язувального рядка на (-2) і додаванням до відповідних елементів другого рядка) обчислимо всі елементи першого та другого рядків, у тому числі і елементи стовпця контрольної суми (розв’язувальний рядок залишається без змін). У результаті виконаних дій одержуємо одиничний вектор у розв’язувальному стовпці. Робимо перевірку правильності розрахунків, порівнюючи суму елементів кожного рядка з відповідним елементом контрольного стовпця. На другому кроці розв’язувальним елементом може бути обраний будь-який, що не розташований у третьому рядку та першому стовпці, так як на першому кроці розв’язувальним був елемент а31. Обираємо, наприклад, а12 (тепер розв’язувальний рядок – перший). Слід звернути увагу на коефіцієнт при розв’язувальному елементі: він повинен дорівнювати одиниці. Щоб виконати дану умову, необхідно елементи розв’язувального рядка помножити на 1/3, і далі виконувати дії, як і на попередньому кроці. Таким чином, одержимо три одиничних вектори у перших трьох стовпцях розрахункової таблиці. Розв’язок системи знайдемо у стовпці вільних членів (bі) проти відповідних одиниць ( з першого рядка: у = -2, з другого рядка: z = 1, з третього рядка: х = 2).
Відповідь: x = 2, y = -2, z = 1.
3.7. Дослідити систему на сумісність.
Виконаємо елементарні перетворення над розширеною матрицею системи:
Визначимо ранг матриці А, розширеної матриці та кількість невідомих системи рівнянь: r (A) = r (A*) = n = 3 За теоремою Кронекера-Капеллі система визначена і сумісна.
Поиск по сайту: |



 . Визначник матриці А не дорівнює нулю, тому матриця А має обернену. Обчислимо алгебраїчні доповнення всіх елементів матриці:
. Визначник матриці А не дорівнює нулю, тому матриця А має обернену. Обчислимо алгебраїчні доповнення всіх елементів матриці:
 ,
, 

 .
.
 .
.







 і виключаємо х2 з третього рівняння
і виключаємо х2 з третього рівняння

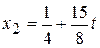
 .
. ,
, - будь-яке число.
- будь-яке число.

 .
.