 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основні властивості визначників
Визначник не зміниться, якщо його рядки поміняти місцями з відповідними стовпцями. При переставленні місцями будь-яких двох рядків визначник змінює знак на протилежний. Якщо відповідні елементи двох рядків визначника рівні або пропорціональні, то визначник дорівнює нулю. Якщо всі елементи якого-небудь рядка дорівнюють нулю, то визначник дорівнює нулю. Загальний множник всіх елементів рядка можна винести за знак визначника. Якщо кожний елемент деякого рядка визначника є сумою двох доданків, то цей визначник дорівнює сумі двох визначників, в одному з яких у тому ж рядку стоять перші доданки, а у другому – другі. Інші рядки у обох визначників однакові та співпадають з відповідними рядками даного визначника. Величина визначника не зміниться, якщо до елементів одного рядка додати відповідні елементи іншого рядка, помножені на одне й те ж саме число. Мінор Mij елемента аij визначника – це визначник, який одержано з даноговикресленням і-го рядка та j-го стовпця, на перетині яких знаходиться елемент. Алгебраїчне доповнення Аij елемента аij – це мінор Мij цього елемента, взятий з відповідним знаком за схемою Теорема (про розкладання визначника за елементами рядка або стовпця).Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення. Система т лінійних рівнянь з п невідомими має вигляд:
де
де при невідомих,
Розв’яком системи (1)називається така сукупність n чисел
Розглянемо систему трьох лінійних рівнянь з трьома невідомими:
Визначник
Складемо визначники:
Теорема (Крамера).Якщо визначник системи (2) не дорівнює нулю, то система має єдиний розв’язок, який знаходиться за формулами:
Матрицю А-1 називають оберненою по відношенню до квадратної матриці А, якщо
де Е – одинична матриця. Для того, щоб квадратна матриця А мала обернену, необхідно і достатньо, щоб визначник
Формула для знаходження оберненої матриці: де Матричний метод:Розв’язок квадратної системи (1’), визначник якої не дорівнює нулю, знаходиться за формулою:
Дві системи рівнянь називаються рівносильними,якщо вони мають однакову множину розв’язків. Від даної системи до рівносильної їй можна прийти за допомогою еквівалентних перетворень систем рівнянь, до яких відносяться множення обох частин рівнянь на ненульове число та складання відповідних частин рівнянь системи. Метод Гаусса(метод послідовних виключень) полягає в тому, що за допомогою елементарних перетворень система рівнянь приводиться до рівносильної системи ступінчастого (або трикутного) вигляду, з якої послідовно, починаючи з останніх за номером змінних, знаходяться усі інші змінні. Метод Жордана-Гаусса(метод повного виключення) полягає в тому, що за допомогою елементарних перетворень система рівнянь приводиться до рівносильної системи діагонального вигляду.
Розглянемо матрицю
Виділимо в ній будь-які k рядків та k стовпців. Елементи, розміщені на їх перетині, утворюють квадратну матрицю k –го порядку; визначник цієї матриці називається мінором k–го порядку матриці А. Рангом r(A) матриці Aназивається найбільший порядок відмінних від нуля мінорів цієї матриці. При знаходженні рангу користуються тим , що ранг не змінюється при виконанні елементарних перетворень над матрицею, до яких відносяться такі операції: 1) переставлення місцями будь-яких двох рядків (стовпців); 2) множення усіх елементів будь-якого рядка (стовпця) на відмінне від нуля число; 3) додавання до усіх елементів деякого рядка (стовпця) матриці відповідних елементів іншого рядка (стовпця), помножених на одне й те саме число; 4) відкидання нульового рядка (стовпця).
2. Матриця Теорема (Кронекера-Капеллі).Система лінійних рівнянь (1) сумісна тоді і лише тоді, коли ранг розширеної матриці системи дорівнює рангу матриці системи:
Перед виконанням завдання № 1 рекомендується опрацювати приклади 3.1-3.7 глави ІІ.
Поиск по сайту: |
 .
. (1)
(1) - дійсні числа, які називають коефіцієнтами системи,
- дійсні числа, які називають коефіцієнтами системи,  , i =1,…,m - вільні члени або праві частини рівнянь,
, i =1,…,m - вільні члени або праві частини рівнянь,  , j=1,…,n - невідомі. Якщо n=m, то система називається квадратною. Запис системи (1) в матричному вигляді:
, j=1,…,n - невідомі. Якщо n=m, то система називається квадратною. Запис системи (1) в матричному вигляді: , (1’)
, (1’) – матриця системи, складена із коефіцієнтів
– матриця системи, складена із коефіцієнтів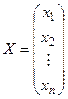 - вектор-стовпець невідомих,
- вектор-стовпець невідомих,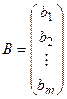 - вектор-стовпець вільних членів.
- вектор-стовпець вільних членів. , при підстановці яких кожне рівняння системи перетворюється на вірну рівність.
, при підстановці яких кожне рівняння системи перетворюється на вірну рівність.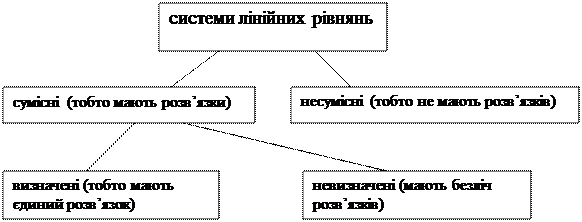
 (2)
(2)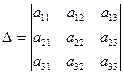 називається визначником системи (2).
називається визначником системи (2).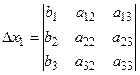 ,
,  .
. .
. ,
, матриці А не дорівнював нулю.
матриці А не дорівнював нулю.
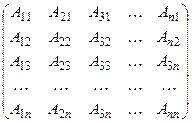 ,
, - алгебраїчні доповнення елементів аij.
- алгебраїчні доповнення елементів аij. .
. називається розширеною матрицею системи (1).
називається розширеною матрицею системи (1).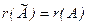 .
.