 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рекомендації до розв’язання типових прикладів розділу 2
2.1. На випуск одиниці двох видів продукції А1, А2 витрачаються комплектуючі В1, В2, В3, В4 у кількостях, що задаються матрицею
У свою чергу, на складання одиниці виробів В1, В2, В3, В4 витрачається продукція С1, С2, С3, задана матрицею
Визначити потрібну кількість елементів D1, D2, D3 вихідного матеріалу, коли відомо, що витрати їх на одиницю С1, С2, С3 задано матрицею
Матрицею витрат елементів D1, D2, D3 на одиницю кінцевої продукції А1 та А2 можна подати у вигляді добутку матриць K= S3·S2·S1, тобто
Знаючи виробничу програму випуску кінцевої продукції, можна визначити потрібну кількість вихідного матеріалу. Наприклад, якщо треба випустити готову продукцію А1=50, а А2=100 одиниць, то для цього матрицю K множимо на вектор
2.2. Три фірми випускають4 види виробів. Задано матриці випуску продукції в липні і серпні:
де аiкі bik Розв’язання: Обсяг продажу продукції на кожній фірмі за місяць: C = B – A Відповідь: місячний обсяг продажу виробів на кожній фірмі 2.3. Підприємство випускає три види продукції, що характеризуються матрицей ‑ планом Х = (1074). При випуску продукції використовують 5типів сировини. Задано матрицю витрат сировини: A = (aik) = S = а) необхідну кількість одиниць сировини кожного виду для забезпечення плану; б) вартість сировини для одиниці кожного виду продукції; в) загальну вартість сировини при виконанні плану випуску Х. Розв’язання: a) Знайдемо необхідну кількість одиниць сировини кожного виду для забезпечення плану С = Х б) Знайдемо вартість сировини для одиниці кожного виду продукції D = S в) Знайдемо загальну вартість сировини при виконанні плану випуску Х F = X 2.4. Виконати розрахунок заробітної плати, що припадає на кожне замовлення при виробництві різноманітних виробів, користуючись даними таких таблиць:
Розв’язання: Визначимо матриці: Q - кількість виробів, P – витрати робочого часу на кожне з робочих місць, J - годинна зарплата: Q = і виконаємо розрахунок зарплати (Q× P) × J = Відповідь: нарахування заробітної плати на замовлення K – 120, 52 гр.од., на замовлення L – 56,36 гр.од.; на замовлення M – 80, 01 гр.од.
2.5. Обчислити визначник
а) за правилом трикутника:
б) розкладанням за елементами першого рядка:
а11 = 1; А11 = (-1)1+1 ·
а12 = 0; а13 = 3, А13 = (-1)1+1 ·
2.6. Знайти обернену матрицю до матриці
Для визначника третього порядку знаки алгебраїчних доповнень будуть такими:
Виконаємо необхідні обчислення для відшукання оберненої матриці. Спочатку обчислимо її визначник, щоб переконатися, що обернена матриця існує: detA=4–2–6+1= –3.
Враховуючи чергування знаків в алгебраїчних доповненнях, дістанемо
Отже, матриця, обернена до матриці A, має такий вигляд:
Правильність знайденої оберненої матриці перевіряємо множенням матриці Aна обернену ліворуч або праворуч:
Поиск по сайту: |
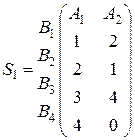 .
.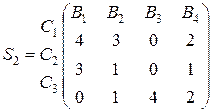 .
. .
.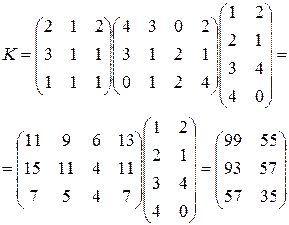 .
.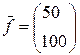 . Отже,
. Отже,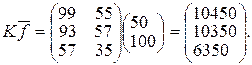
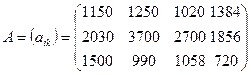 ,
, 
 (i = 1, 2, 3; k = 1, 2, 3, 4) - накопичений з початку року на кінець деякого місяця обсяг продажу виробів відповідного виду по одній фірмі. Знайти обсяг продажу виробів за місяць на кожній фірмі.
(i = 1, 2, 3; k = 1, 2, 3, 4) - накопичений з початку року на кінець деякого місяця обсяг продажу виробів відповідного виду по одній фірмі. Знайти обсяг продажу виробів за місяць на кожній фірмі. .
.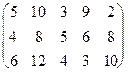
 , де aik ‑ витрати сировини на одну одиницю продукції визначеного виду (к ‑ тип сировини, i ‑ вид продукції). Матриця
, де aik ‑ витрати сировини на одну одиницю продукції визначеного виду (к ‑ тип сировини, i ‑ вид продукції). Матриця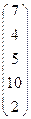 задає вартість однієї одиниці кожного виду сировини. Визначити:
задає вартість однієї одиниці кожного виду сировини. Визначити: А =
А =  =
= 

 .
.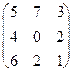 , P =
, P =  , J =
, J =  ,
,


 = 1 · 1 · 7 + 0 · 1 · 4 + (-2) · 5 · 3 – 4 · 3 ·1 – 7 · (-2) · 0 – 1 ·1 · 5 = - 40 ;
= 1 · 1 · 7 + 0 · 1 · 4 + (-2) · 5 · 3 – 4 · 3 ·1 – 7 · (-2) · 0 – 1 ·1 · 5 = - 40 ; = 1· (7 – 5) = 2 ;
= 1· (7 – 5) = 2 ; = 1· (-10 – 4) = -14 ;
= 1· (-10 – 4) = -14 ; .
. .
.








 .
. .
.