 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Явление сверхпроводимости
В предыдущих главах мы изучали квантово-механические явления на микроскопическом уровне. Оказывается, что в таких эффектах, как сверхпроводимость металлов и текучесть жидкого гелия, квантово-механические эффекты проявляются в макроскопических масштабах. Явление сверхпроводимости состоит в том, что при температурах, меньших некоторой критической, сопротивление ряда металлов и сплавов скачком уменьшается до нуля. Это явление было открыто в 1911 г. Камеринг-Оннесом. Отметим некоторые свойства сверхпроводников.
1. Сверхпроводящее состояние наблюдается в интервале температур от 0 до Tкр. При T=Tкр сопротивление скачком увеличивается до некоторого значения R¹0 и при дальнейшем росте температуры линейно возрастает. У нормального металла, т.е. металла, не переходящего в сверхпроводящее состояние, при T®0 сопротивление стремится к некоторому остаточному сопротивлению R0¹0, которое обусловлено рассеянием электронов на дефектах кристаллической решетки (рис. 34.1). 2. При пропускании через сверхпроводник тока создается магнитное поле и, когда индукция магнитного поля становится равной Bкр, сверхпроводящее состояние разрушается. Таким образом, значение сверхпроводящего тока ограничено сверху некоторым значением Bкр. 3. Различают сверхпроводники первого и второго рода. Сверхпроводники первого рода (чистые металлы) однородны по структуре и сверхпроводящее состояние у них возникает во всем объеме. Сверхпроводники второго рода (некоторые сплавы) в относительно слабых магнитных полях становятся неоднородными и разбиваются на сверхпроводящие зоны (области) и зоны нормального металла. Следует отметить также, что у сверхпроводников второго рода сверхпроводящие зоны могут сохраняться даже в очень сильных магнитных полях, что важно для практических целей. 4. Для сверхпроводников первого рода характерен эффект Мейснера, который состоит в том, что в процессе охлаждения металла в магнитном поле в момент перехода его в сверхпроводящее состояние магнитное поле полностью вытесняется из его объема. Это означает, что в сверхпроводнике может протекать только поверхностный ток (толщина слоя проводимости ~10-8 м). Магнитное поле этого тока компенсирует внешнее магнитное поле, так что внутри сверхпроводника полное поле равно нулю. Теория сверхпроводимости была создана в 1957 г. Д. Бардиным, Л. Купером и Д. Шриффером (теория БКШ) и усовершенствована Н.Н. Боголюбовым. Основная идея теории БКШ следующая. Двигающиеся в металле электроны окружены «облаком» положительного заряда, возникающего из-за притяжения к ним положительных ионов кристаллической решетки. К такой системе (электрон — «облако» положительного заряда) может быть притянут какой-либо другой электрон, который также окружен «облаком» положительного заряда. В том случае, если спины электронов противоположны, такая связь является устойчивой и образуется так называемая куперовская электронная пара. Поскольку спин куперовской пары равен нулю, то куперовские пары являются бозонами и при снижении температуры до 0 К они располагаются на самом низшем энергетическом уровне. Энергию связи куперовской пары обозначают 2D. В отличие от нормального металла у сверхпроводников между заполненными и незаполненными состояниями есть энергетическая щель шириной 2D (рис. 34.2).
Рис. 34.2 Рассеяние одного из электронов пары на неоднородности кристалла означало бы разрыв связи, на что необходима энергия 2D. При низких температурах и малых скоростях движения электрону неоткуда взять энергию для разрыва этой связи. В этих условиях куперовские пары могут свободно, без столкновений двигаться по всему кристаллу. Это означает полное отсутствие сопротивления: R=0. При повышении температуры ширина энергетической щели уменьшается и при T=Tкр значение 2D становится равным нулю — сверхпроводимость исчезает. Значения критической температуры Tкр для большинства металлов и сплавов очень малы. Например, для ниобия Tкр=9, свинца — 7,2 K, вольфрама — 0,01 K. Долгое время рекордное значение Tкр имела пленка из соединения Nb3Ge: Tкр=23 K. В 1986 г. сначала Г. Беднорз и А. Мюллер, а затем Р. Чу открыли высокотемпературную сверхпроводимость для соединений типа керамик, состоящих из смеси оксидов. Так, для керамики La2O3×BaO×CuO Tкр=33 K, а для керамики YO3×BaO×CuO Tкр=90 K. В 1988 г. было достигнуто рекордное значение Tкр=128 K. Механизм образование куперовских пар в высокотемпературных сверхпроводниках пока неясен — исследования в этом направлении продолжаются.
Как было отмечено, сверхпроводимость представляет собой явление, в котором квантово-механические эффекты обнаруживаются не в микроскопических, а в крупных, макроскопических масштабах. Особенно наглядно макроскопические квантовые свойства выражены в эффекте квантования магнитного потока в сверхпроводящем кольце с током. Установлено, что если через тороидальное сверхпроводящее кольцо пропустить электрический ток (рис. 34.3), то поток магнитного поля F через поверхность, охватываемую кольцом, может принимать лишь дискретные значения F=nF0, где Механизм квантования магнитного потока рассмотрен в прил. 9. В заключение рассмотрим некоторые практические применения явления сверхпроводимости. Для сглаживания пиков потребления электроэнергии уже сейчас используются сверхпроводящие индукционные носители (спины), которые могут аккумулировать до 4×103 кВт×ч, успешно конкурируя с гидроаккумулирующими агрегатами; созданы опытные образцы сверхпроводящих линий электропередачи, которые по стоимости превышают обычные всего в 2 раза. Сверхпроводники используют также при конструировании некоторых типов электрогенераторов, при создании транспортных систем. Особо следует выделить использование сверхпроводников в информатике и конструировании высокочувствительных приборов для измерения малых температур, слабых магнитных полей и др. Эффект Джозефсона Тонкий слой диэлектрика (обычно пленка окиси металла толщиной 1...2 нм), разделяющий два проводника, называется туннельным контактом.
В 1962 г. Б. Джозефсон теоретически предсказал возможность протекание сверхпроводящего тока через туннельный контакт. Схема для наблюдения эффекта Джозефсона показана на рис. 34.4. Напряжение, подаваемое на туннельный контакт, можно регулировать с помощью переменного сопротивления R. Вольтметр V показывает падение напряжения на туннельном контакте. Различают стационарный и нестационарный эффекты Джозефсона. Стационарный эффект состоит в том, что если ток через туннельный контакт не превышает некоторого критического значения I<Iкр, то падение напряжения на контакте равно нулю. Механизм этого явления состоит в следующем. При наложении внешнего электрического поля на контакт происходит смещение уровней энергии куперовских пар. Пусть величина смещения меньше энергетического зазора между заполненными и незаполненными уровнями, т.е. 2eU<2D (рис. 34.5, а). Тогда куперовская пара из одного сверхпроводника может туннелировать через слой диэлектрика в другой сверхпроводник. Поскольку куперовские пары являются бозонами, то такой процесс возможен даже тогда, когда соответствующий уровень энергии второго сверхпроводника занят.
Процесс туннелирования куперовской пары протекает без ее разрушения и сверхпроводимость туннельного контакта сохраняется, т.е. его сопротивление R=0, и, следовательно, падения напряжения на контакте U = IR = = I× 0 = 0. Нестационарный эффект Джозефсона состоит в том, что если через туннельный контакт пропустить электрический ток, больший критического, то на контакте возникает падения напряжения и контакт излучает электромагнитные волны. Критическому току соответствует некоторое напряжение U, при котором смещение уровней энергии куперовских пар становится равным ширине энергетического зазора между заполненными и незаполненными уровнями энергии: 2eU=2D (рис. 34.5, б). При туннелировании через контакт куперовская пара из верхнего заполненного уровня одного сверхпроводника попадает на нижний незаполненный уровень другого сверхпроводника и, следовательно, обладает избытком энергии по сравнению с другими куперовскими парами. Единственная возможность избавиться от избытка энергии состоит в излучении кванта электромагнитного излучения с энергией hn = 2eU. Таким образом, контакт излучает электромагнитные волны с частотой
Измерив на опыте частоту электромагнитного излучения, из соотношения (34.1) можно найти отношение двух фундаментальных констант Сверхпроводящее кольцо, разделенное двумя тонкими слоями из нормального металла, используется как устройство (называемое сквидом) для измерения слабых магнитных полей (до 10–18 Тл), малых токов (до 10–10 A) и напряжений (до 10–15 В). Высокая чувствительность таких приборов объясняется тем, что критический ток периодически зависит от внешнего магнитного поля (с периодом, равным кванту потока F0). Эффект Джозефсона лежит в основе детекторов СВЧ, быстродействующих логических устройств ЭВМ и др. Сверхтекучесть В 1938 г. П.Л. Капица обнаружил удивительную способность жидкого гелия при температурах T < Tкр=2,17 K протекать без трения через столь узкие капилляры (диаметром ~10–5 см), что обычная жидкость через такие узкие каналы не протекает вследствие ее вязкости и связанного с этим трения о стенки капилляра. Это явление было названо сверхтекучестью. Опыты показывают, что в процессе охлаждения жидкого гелия при некоторой температуре T = Tкр скачком изменяется его удельная теплоемкость, плотность коэффициент теплового расширения без выделения или поглощения теплоты. Поэтому переход жидкого гелия из обычного состояния в сверхтекучее является фазовым переходом второго рода (см. п. 10.4). Жидкий гелий, находящийся при температурах меньше критической (T < Tкр) в сверхтекучем состоянии, называют He II (гелий-два), в отличие от He I (гелий-один) — обычного жидкого гелия. Явление сверхтекучести проявляется не только при течении He II сквозь тонкие капилляры и узкие щели, но и при перетекании его из сосуда в сосуд непосредственно по их стенкам. Поместим пробирку со сверхтекучим гелием в ванну, заполненную, как и пробирка, He II. Если уровень жидкости в пробирке ниже, чем в ванне, то He II перетекает из ванны по стенкам пробирки до тех пор, пока уровни жидкости в пробирке и ванне не сравняются. Аналогичный эффект наблюдается, если уровень He II в пробирке выше, чем в ванне. Если же пробирку вынуть из ванны, то сверхтекучий гелий самопроизвольно начнет вытекать через край пробирки, потечет по ее внешним стенкам вниз с последующим образованием капель, падающих в ванну с нижнего конца пробирки. Теория сверхтекучести была разработана в 1941 г. Л.Д. Ландау, который предложил двужидкостную модель He II, состоящую из нормальной и сверхтекучей компонент. Атомы He4 имеют целочисленный спин и относятся к бозонам. При температурах ниже критической значительная часть атомов He4 переходит в состояние с наименьшей энергией — образуется так называемый бозе-конденсат. Все частицы бозе-конденсата описываются одной и той же волновой функцией, обладают одинаковой энергией и импульсом и поэтому их движение согласовано (когерентно). Бозе-конденсат образует сверхтекучую компоненту He II, а совокупность атомов, не вошедших в бозе-конденсат, составляет нормальную компоненту. Движение нормальной компоненты характеризуется всеми обычными свойствами течения вязкой жидкости, в то время как движение сверхтекучей компоненты как раз и ответственно за явление сверхтекучести. Из такой двужидкостной модели следует, что при вращении сосуда, заполненного He II, не имеющая вязкости сверхтекучая компонента должна оставаться неподвижной, а во вращательное движение будет вовлекаться его нормальная компонента. Однако, опыты показывают, что при достаточно больших скоростях вращения сосуда сверхтекучая компонента также вовлекается во вращательное движение. Такое поведение сверхтекучей компоненты объясняется ее взаимодействием с нормальной компонентой, приводящим к вовлечению первой из них во вращательное движение. При этом, как показали Л. Онсагер и Р Фейнман (1957 г.), вращательное движение сверхтекучей компоненты должно быть квантованным и его можно описать уравнением, аналогичным уравнению первого постулата Бора:
или
m — масса атома He4; l — длина окружности, которую описывает атом гелия. Из этого следует, что под влиянием внешнего воздействия скорость вращательного движения сверхтекучей компоненты не может изменяться непрерывно, а только скачком:
Эффект скачкообразного изменения скорости вращения сверхтекучей компоненты демонстрирует наличие квантовых свойств макроскопических систем, что было проверено экспериментом. Рассмотрим теперь жидкий гелий, состоящий из атомов изотопа He3, которые относятся к фермионам, поскольку имеют полуцелый спин. Согласно принципу Паули, фермионы не могут находиться в одинаковом состоянии и поэтому, казалось бы, жидкий He3 не может перейти в сверхтекучее состояние. Тем не менее, в 1972 г. сверхтекучесть He3 была установлена (Tкр=2,6×10-3 K, P=34 атм). Сверхтекучесть He3 объясняется тем, что при указанных условиях атомы He3 объединяются в куперовские пары, которые являются бозонами и могут образовывать бозе-конденсат. Аналогичный механизм возникновения сверхтекучести имеет место в нейтронных звездах.
Лекція 48. Основи квантової електронiки Взаємодiя випромiнювання з речовиною. Вимушене випромiнювання. Лазери.
Поиск по сайту: |
 Рис. 34.1
Рис. 34.1
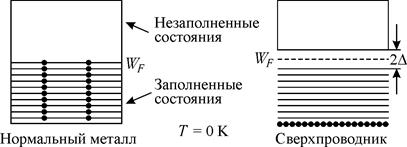
 Рис. 34.3
Рис. 34.3
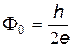 — квант магнитного потока, или флюксон.
— квант магнитного потока, или флюксон. Рис. 34.4
Рис. 34.4
 Рис. 34.5
Рис. 34.5
 .
.
 с точностью, которая значительно превосходит точность измерения другими методами.
с точностью, которая значительно превосходит точность измерения другими методами. (n=0, 1, 2, …),
(n=0, 1, 2, …), .
. .
.