 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 3. Електромагнетне поле. Струми зміщення
Фізичні поняття ·Струм зміщення – це темп зміни потоку електричної індукції
·Вихрове електричне поле – це електричне поле яке виникає внаслідок зміни в часі магнетного поля. ·Магнеторушійна сила– це циркуляція вектора напруженості магнетного поля вздовж замкненого контура
·Хвильове рівняння– це рівняння яке має вигляд
де ·Рівняння хвилі – це функція від координати і часу яка є розв’язком хвильового рівняння. ·Вектор Пойтінга– це вектор напрям якого вказує на напрям перенесення енергії електромагнетною хвилею, а величина дорівнює потужності яка припадає на одиницю площі хвильового фронту.
Постулати Ø Закон повного струму: циркуляція вектора напруженості магнетного поля вздовж будь-якого замкненого контура дорівнює сумі потоку вектора густини струму та потоку темпу зміни вектора електричної індукції через поверхню, яка спирається на цей контур.
Якщо використати означення магнеторушійної сили, струму провідності та струму зміщення, то цей постулат можна сформулювати простіше, а саме: магнеторушійна сила, яка виникає в певному замкненому контурі дорівнює сумі струмів провідності та зміщення що проходять через будь-яку поверхню, яка спирається на цей контур.
Задачі (256) За допомогою теореми Стокса подамо закон повного струму в диференціяльній формі.
Теорема Стокса стверджує, що циркуляція будь-якого вектора вздовж певного замкненого контура дорівнює потоку ротора цього вектора через поверхню, яка спирається на цей контур. Згідно з цією теоремою
а закон повного струму набирає вигляду
або
Оскільки інтегрування в лівій і правій частинах цієї рівності відбувається в одній і тій же області, то з їх рівності випливає рівність підінтегральних виразів, тобто
Ми отримали диференціяльну форму закону повного струму. Другий доданок в цій формулі – це густина струму зміщення.
(257) На основі означень струму провідності та струму зміщення покажемо, що на ділянці кола змінного струму, що містить конденсатор, сила струму в провідниках дорівнює силі струму зміщення між обкладками конденсатора.
Ми отримали, що струм провідності в провідниках дорівнює струму зміщення. Очевидно, що цей струм зміщення оскільки він є темпом зміни потоку вектора електричної індукції локалізований між обкладками конденсатора.
(258) Покажемо, що з рівнянь Максвелла випливає хвильове рівняння. Про диференціюємо закон повного струму за часом (у відсутності струмів провідності).
Підставивши сюди
дістанемо
В це рівняння підставимо закон електромагнетної індукції
Застосувавши формулу
і врахувавши, що в заданій області простору відсутні не тільки струми провідності, а й електричні заряди (
Як і для механічних хвиль можемо позначити
Тоді хвильове рівняння набуває вигляду
Очевидно, що в скалярній формі це рівняння має вигляд
і якщо вектор
Для вектора
(259) Доведемо, що будь-яка функція аргументом якої є Отже функція має вигляд
або узагальнюючи
Знаходимо похідні які фігурують у хвильовому рівнянні (задача 258)
Підставимо отримані другі похідні у хвильове рівняння. Дістанемо тотожність
яка свідчить, що дійсно функція (260) Представимо рівняння електромагнетної хвилі у вигляді
Оскільки будь-яка функція аргументом якої є
де Встановимо як пов’язана стала Міркуємо так. Напруженість поля електромагнетної хвилі набуває свого максимального значення за умови
Умова сусіднього максимуму є
Віднявши від другої рівності першу дістанемо
Але
Підставивши цей вираз в рівняння хвилі (1), дістанемо
або
Застосуємо означення періоду хвилі Т як часу протягом якого хвиля проходить відстань
або
Оскільки хвильове рівняння для вектора
також є рівнянням електромагнетної хвилі причому фази векторів
(261) На основі закону повного струму в диференціяльній формі доведемо, що вектори
Спрямуємо вісь
тому вектор
(262) На основі двох рівнянь Максвела, а саме закону електромагнетної індукції та закону повного струму знайдемо числове значення швидкості електромагнетної хвилі у вакуумі.
Застосуємо до цієї хвилі диференціяльну форму рівнянь Максвела. Позаяк струми провідності відсутні, то закон повного струму має вигляд
Знайдемо по черзі ліву і праву частини цієї рівності
Оскільки вектор
і
Тепер рівняння (1) має вигляд
Ця рівність, очевидно, можлива лише за умови
звідки
або
Закон електромагнетної індукції в диференціальній формі має вигляд
Знову знайдемо окремо ліву і праву частини цієї рівності
Представивши вектор
і на основі закону електромагнетної індукції (3)
Ця рівність можлива лише за умови
звідки
або
З цієї рівності, і рівності (2) та формул зв’язку між векторами напруженості та індукції електричного та магнетного полів дістанемо
звідки
(263) На основі двох рівнянь Максвела, а саме закону електромагнетної індукції та закону повного струму знайдемо вираз для швидкості електромагнетної хвилі в середовищі. Оскільки згадані рівняння Максвела однакові як у вакуумі так і в середовищі, то вивід формули для швидкості електромагнетної хвилі в середовищі буде такий самий як і для вакууму (попередня задача) аж до того моменту, коли нам слід буде використати формули зв’язку між величинам векторів напруженості та індукції відповідних полів, а саме
Таким чином формула для швидкості електромагнетної хвилі в середовищі буде мати вигляд
Позаяк для будь-якого середовища Величину
показує в скільки разів швидкість електромагнетної хвилі у вакуумі більша ніж в розглядуваному середовищі.
(264) На основі формул для густини енергії електричного та магнетного полів знайдемо вираз потужності яка припадає на одиницю площі фронту електромагнетної хвилі. Оскільки електричне і магнетне поле електромагнетної хвилі перебувають в одній і тій же фазі, то енергія цієї хвилі дорівнює сумі енергій електричного та магнетного полів, а об’ємна густина енергії дорівнює сумі відповідних об’ємних густин
Згідно з означенням об’ємної густини енергії
Підставивши сюди
Врахувавши, що
Ліва частина цього рівняння – це потужність яка припадає на одиницю площі фронту хвилі. Позначивши її буквою
Введемо вектор
де
Очевидно, що напрям вектора Пойтінга вказує на напрям в якому переноситься енергія. Додатки
Поиск по сайту: |
 .
.

 –стала величина,
–стала величина, 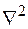 – оператор Лапласа.
– оператор Лапласа.



 .
.
 До ділянки кола з конденсатором (мал. 170) застосуємо послідовно означення сили струму, означення ємності, зв'язок напруженості електричного поля з напругою, формулу ємності плоского конденсатора, зв'язок між напруженістю та індукцією електричного поля та індукцією електричного поля та означенням потоку. Дістанемо
До ділянки кола з конденсатором (мал. 170) застосуємо послідовно означення сили струму, означення ємності, зв'язок напруженості електричного поля з напругою, формулу ємності плоского конденсатора, зв'язок між напруженістю та індукцією електричного поля та індукцією електричного поля та означенням потоку. Дістанемо


 ,
,


 тому
тому  згідно з теоремою Остроградського-Гауса) дістанемо хвильове рівняння
згідно з теоремою Остроградського-Гауса) дістанемо хвильове рівняння



 залежить лише від координати х, хвильове рівняння має вигляд
залежить лише від координати х, хвильове рівняння має вигляд
 отримаємо таке саме рівняння. Для цього слід зі згаданих двох рівнянь Максвелла виключити вектор
отримаємо таке саме рівняння. Для цього слід зі згаданих двох рівнянь Максвелла виключити вектор  (продиференціювати закон електромагнетної індукції і підставити в нього закон повного струму).
(продиференціювати закон електромагнетної індукції і підставити в нього закон повного струму). або
або  є розв’язком хвильового рівняння.
є розв’язком хвильового рівняння. ,
, .
.


 є розв’язком хвильового рівняння.
є розв’язком хвильового рівняння. .
. є розв’язком хвильового рівняння, то і функція
є розв’язком хвильового рівняння, то і функція (1)
(1) – стала величина, є його розв’язком, тобто є вона рівнянням хвилі.
– стала величина, є його розв’язком, тобто є вона рівнянням хвилі.


 – це відстань між двома сусідніми максимумами, тобто довжина хвилі
– це відстань між двома сусідніми максимумами, тобто довжина хвилі  , тому
, тому
 ,
,
 Тепер рівняння хвилі дістає вигляд
Тепер рівняння хвилі дістає вигляд

 взаємно – нормальні.
взаємно – нормальні. вздовж вектора
вздовж вектора  (мал. 172) і обчислимо його ротор.
(мал. 172) і обчислимо його ротор.
 Оскільки вектори
Оскільки вектори  та
та 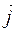 лежать в площині ху то і вектор
лежать в площині ху то і вектор  лежить в цій площині як їх лінійна комбінація, тобто він є нормальним до вектора
лежить в цій площині як їх лінійна комбінація, тобто він є нормальним до вектора 
 , який своєю чергою співнапрямлений з вектором
, який своєю чергою співнапрямлений з вектором  . Отже вектор
. Отже вектор  Поглянемо на хвильовий фронт плоскої електромагнетної хвилі яка поширюється у вакуумі вздовж осі х і візьмемо до уваги, що всі три вектори
Поглянемо на хвильовий фронт плоскої електромагнетної хвилі яка поширюється у вакуумі вздовж осі х і візьмемо до уваги, що всі три вектори  ,
, 
 напрямлений туди куди і вектор
напрямлений туди куди і вектор 


 . З цієї умови і останньої рівності дістанемо
. З цієї умови і останньої рівності дістанемо

 (2)
(2) (3)
(3)
 дістаємо, що
дістаємо, що

 , і тоді
, і тоді ,
,





 та
та  , то швидкість електромагнетної хвилі в середовищі менша ніж у вакуумі.
, то швидкість електромагнетної хвилі в середовищі менша ніж у вакуумі. позначають
позначають  і називають показником заломлення середовища. Бачимо, що показник заломлення
і називають показником заломлення середовища. Бачимо, що показник заломлення



 , де
, де 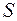 – площа хвильового фронту (мал. 173), помноживши отриману рівність на
– площа хвильового фронту (мал. 173), помноживши отриману рівність на  і поділивши на
і поділивши на  дістанемо
дістанемо

 ,
,  і
і  маємо
маємо
 маємо
маємо

 – одиничний вектор нормалі до хвильового фронту і назвемо його вектором Пойтінга. Бачимо, що вектор Пойтінга напрямлений як і вектор
– одиничний вектор нормалі до хвильового фронту і назвемо його вектором Пойтінга. Бачимо, що вектор Пойтінга напрямлений як і вектор  тому він задовольняє обидвом ознакам вектора який є векторним добутком двох векторів, а саме векторів
тому він задовольняє обидвом ознакам вектора який є векторним добутком двох векторів, а саме векторів 