 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 6. Магнетне поле в речовині
Фізичні явища · Механомагнетний ефект (Ефект Барнета) – це явище намагнечення тіла внаслідок його обертання. · Магнетомеханічний ефект (ефект Ейнштейна-де-Гааза) – це явище обертання тіла внаслідок його намагнечення. · Електронний парамагнетичний резонанс(ЕПР) – це явище поглинання парамагнетиком в магнетному полі електромагнетної хвилі з частотою, яка дорівнює частоті Лармора всіх електронів атома. · Ядерний магнетний резонанс (ЯМР) – це явище поглинання магнетиком у магнетному полі електромагнетної хвилі з частотою, яка дорівнює ларморівській частоті ядра. · Циклотронний резонанс (ЦР) – це явище поглинання вільними електронами твердого тіла в магнетному полі електромагнетної хвилі (фотонів) з частотою, яка дорівнює циклотронній частоті. · Магнетофононний резонанс (МФР) – це явище поглинання вільними електронами твердого тіла в магнетному полі теплової хвилі (фононів) з частотою, яка дорівнює циклотронній частоті. Фізичні поняття ·Орбітальний магнетний момент електрона – магнетний момент, який виникає внаслідок орбітального руху електрона в атомі. ·Спіновий магнетний момент електрона – магнетний момент, яким володіє кожен електрон (вільний чи зв’язаний з атомом). ·Магнетон Бора – це найменше значення орбітального магнетного моменту електрона (позначення ·Гіромагнетне відношення – це відношення орбітального магнетного моменту електрона до його орбітального моменту імпульсу. ·Спінове гіромагнетне відношення – це відношення спінового магнетного моменту електрона до його власного моменту імпульсу. ·Діамагнетик – речовина, у якій кожен атом чи молекула не мають магнетного моменту. ·Парамагнетик – речовина, у якій кожен атом чи молекула мАють магнетний момент, проте будь-який зразок цієї речовини не має магнетного момену. ·Феромагнетик – речовина, кожен атом чи молекула якої має магнетний момент, і в якій існуть мікрообласті (домени) з ненульовим магнетним моментом. Макрозразок цієї речовини може мати або не мати магнетного моменту залежно від його історії перебування в магнетних полях. ·Частота Лармора – це величина, на яку змінюється частота обертання електрона навколо ядра під впливом зовнішнього магнетного поля. ·Магнетний гістерезис – це явище залежності зміни намагнеченості феромагнетика в зовнішньому магнетному полі від його історії намагнечення. ·Точка Кюрі – температура, за якої феромагнетик переходить у парамагнетик. ·Намагнеченість (вектор намагнеченості) – це магнетний момент одиниці об’єму магнетика (позначення j)
·Магнетна сприйнятливість магнетика – це відношення його намагнеченості до напруженості зовнішнього магнетного поля, яка її спричинила (позначення
·Відносна магнетна проникність магнетика – це збільшена на одиницю його магнетна сприйнятливість (позначення
·Антиферомагнетик – речовина, в доменах якої атоми мають попарно протилежні магнетні моменти, а напрями магнетних моментів атомів у різних доменах різні. ·Феримагнетик – це нескомпенсований антиферомагнетик (в межах домена є атоми двох сортів з попарно протилежними за напрямом магнетними моментами, які мають різну величину). ·Множник Ланде (g - фактор) – величина, яка показує, у скільки разів гіромагнетне відношення електрона в атомі є більшим за спінове гіромагнетне відношення. ·Ефективна маса вільного електрона в твердому тілі – це маса такої частинки з зарядом електрона, яка під дією заданої зовнішньої сили набуває такого ж прискорення, як і вільний електрон у твердому тілі під впливом тієї ж зовнішньої сили.
Задачі (202) Знайдемо відношення орбітального магнетного моменту електрона в атомі Оскільки орбітальний момент імпульсу електрона
то магнетний момент представимо також через радіус орбіти Згідно з означенням магнетного моменту
Оскільки струм I створюється одним електроном, то через поперечний переріз уявного провідника за період Т проходить заряд е, тому, згідно з означенням сили струму
З двох останніх рівностей дістанемо
Звідси і з рівності для
Вектор моменту імпульсу спрямований за поступальним рухом правого гвинта, якщо гвинт крутити в напрямі руху електрона (мал. 134), а вектор магнетного моменту знаходимо за тим самим правилом правого гвинта, коли гвинт крутити в напрямі струму. А оскільки еквівалентний руху електрона струм тече проти напряму його руху, то вектор магнетного моменту є протилежним до вектора моменту імпульсу.
(204)Знайдемо числове значення магнетона Бора (на основі квантованості моменту імпульсу). З гіромагнетного відношення
Оскільки орбітальний момент імпульсу квантований
і найменше його значення буде за умови п=1. Це значення і є магнетоном Бора згідно з його означенням, тобто
Отже, магнетон Бора є квантом магнетного моменту.
(205) На основі того факту, що електрон має власний момент ім.пульсу
Отже, спінове гіромагнетне відношення
Очевидно, що, як і для орбітальних моментів, вектори
(206) Установимо, з яких складових складається магнетний момент атома та цілого магнетика. Очевидно, що магнетний момент атома як векторна величина складається з векторної суми магнетних моментів усіх електронів та ядра. Нагадаємо, що магнетний момент окремого електрона, своєю чергою дорівнює сумі орбітального та спінового магнетних моментів. Магнетний момент ядра також складається з його орбітального магнетного моменту (ядра насправді обертаються навколо спільного з електронами центра мас), власного магнетного моменту ядра та власних магнетних моментів нуклонів. Проте оскільки магнетний момент ядра на три порядки менший за магнетний момент електронів (ядерний магнетон Також очевидно, що магнетний момент магнетика (мактротіла) дорівнює сумі магнетних моментів усіх його атомів та вільних електронів (якщо такі є), кожен з яких володіє спіновим магнетним моментом.
(207) Покажемо, що гіромагнетне відношення електрона в атомі не дорівнює ні спіновому, ні орбітальному гіромагнетному відношеньню. Очевидно, що для вільного електрона, який має лише спіновий момент імпульсу та спіновий магнетний момент, гіромагнетне відношення дорівнює спіновому гіромагнетному відношенню, тобто
де g – множник Ланде (g – фактор), який для електрона в атомі Якщо в атомі не один електрон, то це гіромагнетне відношення яке тепер дорівнює відношенню сумарного магнетного моменту всіх електронів до такого ж сумарного моменту імпульсу можна трактувати як гіромагнетне відношення атома (якщо знехтувати магнетним і механічним моментом ядра).
(208) Покласифікуємо всі магнетики на діа- пара- та феромагнетики з погляду наявності магнетних моментів у їхніх електронів, атомів, мікро- та макрообластей.
Якщо ж кожен атом магнетика має магнетний момент, то це ще не означає, що магнетик має магнетний момент. Дійсно, внаслідок того, що магнетні моменти атомів спрямовані хаотично, то їхня сума величезної кількості доданків практично дорівнює нулеві, що означає, що парамагнетик, як і діамагнетик загалом, не має магнетного моменту (мал. 135 (а)). У феромагнетику, на відміну від парамагнетика, немає цілковитого хаосу в напрямах магнетних моментів атомів – там є цілі мікрообласті (домени), у яких магнетні моменти атомів упорядковані (мал. 135 (б)). Проте оскільки магнетні моменти окремих доменів спрямовані хаотично, то феромагнетик загалом, як і діа- та парамагнетик, не має магнетного моменту.
(209) З’ясуємо механізм виникнення доменів у феромагнетику.
Цей механізм подібний до механізму виникнення доменів у сегнетоелектрику. Може статися так, що в якийсь момент часу магнетні моменти двох сусідніх атомів виявляться співнапрямленими. При цьому магнетне поле, створене відповідними молекулярними струмами цих атомів, підсилить. Тоді під впливом цього поля упорядкується третій, четвертий і п’ятий атом, причому, що більше магнетних моментів упорядкується, то стійкішою стає ця система й активніше спонукає до упорядкування інші атоми. На перший погляд видається, що це упорядкування магнетних моментів має поширитися на весь кристал. Проте взявши до уваги те, що в інших областях кристалу виникають подібні флуктуації магнетного моменту, які поводяться так само, доходимо висновку, що весь кристал буде поділений на області з упорядкованими магнетними моментами, причому їхні напрями будуть різні в різних областях (доменах). Очевидно, що розміри цих областей будуть більші, що менша ймовірність виникнення флуктуації магнетного моменту.
(210) Покажемо, як за приблизними розмірами домену у феромагнетику можна знайти ймовірність його виникнення і навпаки. За означенням ймовірності, ймовірність виникнення домену
де
звідки бачимо, що більша ймовірність виникнення домену, то менший його об’єм.
(211) З’ясуємо природу діамагнетного ефекту, тобто покажемо, що діамагнетик намагнечується проти зовнішнього магнетного поля, що означає, що магнетне поле в діамагнетику послаблюється. Спочатку покажемо, що в магнетному полі електрони в одних атомах діамагнетика сповільнюють свою орбітальну швидкість, а в інших – прискорюють. Для цього поділимо атоми діамагнетика, який потрапив у магнетне поле, на два типи: ті, для яких нормальна до площини орбіти складова вектора індукції зовнішнього магнетного поля
З мал. 136 видно, що орбітальна швидкість електрона в атомі першого типу зменшується, а другого – збільшується. Дійсно, в магнетному полі до електричної сили притягання до ядра  та відцентрової сили інерції та відцентрової сили інерції 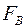 додається ще сила магнетного поля додається ще сила магнетного поля  , яка в першому випадку спрямована від центра, а в другому – до центра. Тоді рівнодійна сила вже не дорівнює нулеві і електрон починає сходити з орбіти: в першому випадку від ядра, а в другому – до нього. Як видно з того ж малюнка, це сходження з орбіти спричиняє виникнення рівнодійної сили , яка в першому випадку спрямована від центра, а в другому – до центра. Тоді рівнодійна сила вже не дорівнює нулеві і електрон починає сходити з орбіти: в першому випадку від ядра, а в другому – до нього. Як видно з того ж малюнка, це сходження з орбіти спричиняє виникнення рівнодійної сили  , яка в першому випадку гальмує орбітальний рух електрона, а в другому – прискорює. Це гальмування в першому випадку (мал. 136, а) приводить до зменшення орбітального магнетного моменту, а оскільки спіновий магнетний момент залишається незмінним, то результативний магнетний момент спрямований в бік спінового, тобто проти поля. У другому випадку (мал. 136, б) орбітальний магнетний момент зростає і результативний магнетний момент спрямований в бік орбітального, тобто знову ж таки проти зовнішнього поля (пам’ятаємо, що напрям орбітального магнетного моменту знаходимо, як напрям нормалі до площини струму). Отже, магнетне поле в діамагнетику послаблюється. , яка в першому випадку гальмує орбітальний рух електрона, а в другому – прискорює. Це гальмування в першому випадку (мал. 136, а) приводить до зменшення орбітального магнетного моменту, а оскільки спіновий магнетний момент залишається незмінним, то результативний магнетний момент спрямований в бік спінового, тобто проти поля. У другому випадку (мал. 136, б) орбітальний магнетний момент зростає і результативний магнетний момент спрямований в бік орбітального, тобто знову ж таки проти зовнішнього поля (пам’ятаємо, що напрям орбітального магнетного моменту знаходимо, як напрям нормалі до площини струму). Отже, магнетне поле в діамагнетику послаблюється.
Насправді електрон не сходить зі своєї орбіти, це забороняється квантовою фізикою, тому єдиним результатом дії магнетного поля є сповільнення чи прискорення його орбітального руху саме для того, щоб відцентрова сила інерції своїм зменшенням чи збільшенням забезпечила рівність нулеві рівнодійної сили. Ті електрони які рухаються під кутом до силових ліній очевидно мають рухатися гвинтовими лініями (задача 178). Проте, вони водночас рухаються навколо ядра атома. Оскільки електрон в атомі не може плавно змінити своєї орбіти (це заборонено квантовою механікою), то результатом цих двох рухів є поворот цілої площини орбіти електрона – так звана прецесія орбіти. При цьому вектор орбітального магнетного моменту описує конус навколо вектора індукції зовнішнього магнетного поля.
(212) Знайдемо вираз для зміни орбітальної частоти електрона в зовнішньому магнетному полі (частоти Лармора). Для цього напишемо основне рівняння динаміки в неінерційних системах відліку (НСВ) за відсутності та присутності магнетного поля. За відсутності магнетного поля сила електричного притягання електрона до ядра зрівноважується відцентровою силою інерції
або
де Як ми вже з’ясували (попередня задача), у зовнішньому магнетному полі орбітальна частота електрона змінюється. Позначимо її
або
Представивши лінійну швидкість через кутову, маємо
Віднявши рівняння (1) і (2), дістанемо
Оскільки
тоді
звідки
Це і є зміна орбітальної частоти електрона в зовнішньому магнетному полі, або інакше: величина, на яку зменшується чи збільшується орбітальна частота електрона під впливом зовнішнього магнетного поля. Цікаво приблизно обчислити цю зміну частоти в магнетному полі і порівняти її з частотою за відсутності поля. Для Очевидно, що так само мало змінюється і орбітальний магнетний момент електрона.
(213) Знайдемо зміну орбітального магнетного моменту електрона в магнетному полі. Зміна орбітальної частоти електрона спричиняє зміну його орбітального магнетного моменту. До внесення в магнетне поле, цей магнетний момент
Після зміни частоти на
Підставивши сюди вираз для частоти Лармора
Відносна його зміна
Бачимо, що зміна орбітального магнетного моменту така ж, як і зміна частоти обертання електора, а оскільки вона дуже мала (попередня задача), то діамагнетний ефект є дуже слабкий.
(214) Покажемо, що в пара- та феромагнетику магнетне поле підсилюється. Дійсно, атоми пара - чи феромагнетика володіють магнетним моментом, тому їхні магнетні моменти орієнтуються за силовими лініями поля, тим самим підсиливши його (задача 151 про вільний контур зі струмом в магнетному полі). Очевидно, що в пара - чи феромагнетику, як і в діамагнетику, також відбувається зміна орбітальної частоти електрона, проте вона, як ми показали (попередня задача), є дуже малою і тому практично не впливає на загальний ефект.
(215) Покажемо, що у феромагнетику на відміну від діа- чи парамагнетика, після виключення зовнішнього магнетного поля упорядкованість магнетних моментів не зникає цілком, тобто їм властиве явище гістерезису. Згадаємо механізм утворення домену: в деякій точці феромагнетика виникає досить сильна флуктуація магнетного поля унаслідок випадково однакової орієнтації двох чи більше магнетних моментів. У цьому полі магнетні моменти інших атомів також повертаються у напрямі поля і це поле стає ще сильнішим. Тоді воно легко зорієнтовує інші магнетні моменти і т.д. Цей процес поширюється у речовині, доки не натрапить на межу іншого домена. У межах одного домена напрям магнетних моментів не змінюється з часом, тобто він є стійким. Коли включається магнетне поле, магнетні моменти всіх доменів повертаються в напрямі поля, тобто весь магнетик стає одним великим доменом. Але як ми з’ясували, напрям магнетного моменту в домені є стійким і без поля, тому він залишається таким і після виключення зовнішнього магнетного поля. Проте ця упорядкованість буде частковою внаслідок руйнівної дії хаотичних теплових рухів атомів.
(216) Покажемо, що пара- та феромагнетику властиве насичення магнетного моменту в зовнішньому магнетному полі, тобто явище незростання магнетного моменту, починаючи з певних значень напруженості зовнішнього магнетного поля. Магнетний момент магнетика дорівнює сумі магнетних моментів усіх атомів або всіх доменів у випадку феромагнетика, тому коли зовнішне магнетне поле є достатньо сильним, щоб зорієнтувати магнетні моменти цих усіх атомів чи доменів в одному напрямі, то наступне збільшення індукції зовнішнього магнетного поля вже не приводить до збільшення магнетного момену.
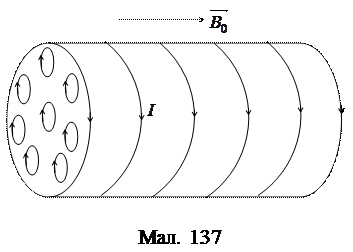
(217) Покажемо, що в магнетиках зовнішнє магнетне поле підсилюється в
 , паралельному до його осі (мал. 137). , паралельному до його осі (мал. 137).
Під впливом зовнішнього магнетного поля його магнетні моменти будуть упорядковані, тому і площини відповідних мікрострумів будуть упорядковані. Згідно з принципом суперпозиції полів, індукція магнетного поля всередині магнетика
З малюнка видно, що магнетні поля мікрострумів всередині магнетика компенсують один одного, а по краях – ні, тому весь магнетик ми можемо розглядати, як соленоїд з одним шаром витків зі струмом I, і густотою витків n. Тому
де ми послідовно застосували формулу магнетного поля соленоїда, означення густоти витків, означення магнетного моменту, означення намагнеченості, означення магнетної сприйнятливості та формулу зв’язку між напруженістю та індукцією магнетного поля. Для вектора
Підставивши останню формулу в (1), дістанемо
звідки бачимо, що в діамагнетиках, оскільки
(218) Оцінимо межі, у яких лежать магнетні сприйнятливості різних магнетиків.
Парамагнетики намагнечуються у напрямі зовнішнього магнетного поля (задача 210), тому для них Те ж саме стосується і феромагнетиків лише з тією різницею, що оскільки атоми феромагнетиків мають значний магнетний момент, то
(219) Пояснимо експериментальну криву магнетного гістерезису. На мал. 139 показана експериментальна крива магнетного гістерезису, тобто експериментальна залежність намагнеченості J від напруженості зовнішнього магнетного поля З цього графіка видно, що зі збільшенням індукції зовнішнього магнетного поля намагнеченість зростає, причому нелінійно, що говорить про те, що магнетна проникність не є сталою величиною (згадаємо, що
 не є константою, а функцією від зовнішнього поля, причому за кожного значення індукції цього поля магнетна проникність дорівнює тангенсу кута нахилу дотичної в цій точці до осі не є константою, а функцією від зовнішнього поля, причому за кожного значення індукції цього поля магнетна проникність дорівнює тангенсу кута нахилу дотичної в цій точці до осі  і, як бачимо з графіка, вона спочатку зростає до точки перегину кривої намагнечення, а потім спадає до свого мінімального для феромагнетика значення і, як бачимо з графіка, вона спочатку зростає до точки перегину кривої намагнечення, а потім спадає до свого мінімального для феромагнетика значення 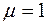 , за якого індукція поля всередині феромагнетика практично досягає насичення (задача 216). Дійсно, оскільки , за якого індукція поля всередині феромагнетика практично досягає насичення (задача 216). Дійсно, оскільки
то за умови насичення ( Якщо після досягнення насичення почати зменшувати індукцію зовнішнього поля, то ми бачимо, що крива не буде повертатися назад тим самим шляхом, а розміститься вище від кривої першого намагнечення. Це відбувається тому, що упорядкованість магнетних моментів доменів не зникає цілком, бо магнетним моментом доменів властива стійкість (задача 215). Коли зовнішнє магнетне поле зменшити до нуля, то поле в феромагнетику не дорівнюватиме нулю (залишкова намагнеченість). Для того, щоб поле у феромагнетику зменшилось до нуля, до нього слід прикласти зовнішнє поле протилежного напряму певної величини (коерцитивна сила). Якщо і надалі збільшувати зовнішнє поле в цьому напрямі, то поле у феромагнетику знову досягне насичення і за наступного зменшення зовнішнього поля все буде повторюватись – крива замкнеться (петля гістерезису). Якщо припинити змінювати зовнішнє поле в точці Як бачимо, намагнеченість феромагнетика залежить від того, в якому зовнішньому полі він перебував до того, тобто залежить від його історії намагнечення.
(220) Покажемо, що існує певна температура, за якої феромагнетик переходить у парамагнетик. Очевидно, що з підвищенням температури все більше проявлятиме себе руйнівна дія хаотичного теплового руху атомів і за певної температури упорядкованість магнетних моментів у доменах буде цілком зруйнована, тобто домени практично зникнуть і феромагнетик перетвориться на парамагнетик. Ця температура називається точкою Кюрі. Наприклад, для нікелю точка Кюрі становить 3580С, для заліза – 7800С, для кобальту – 11500С. Ідея експериментального вимірювання точки Кюрі полягає в тому, що коли нагрівати феромагнетний стержень, який є осердям трансформaтора, то за температури Кюрі магнетний потік в трансформаторі різко знизиться і сила струму у вторинній обмотці різко впаде. (221) Покажемо, що в неоднорідному магнетному полі парамагнетик рухається в бік сильнішого поля, тоді як діамагнетик – в бік слабшого поля (виштовхується з магнетного поля).
Описані явища підтверджуються експериментально. Подібними міркуваннями можна також довести, що в однорідному магнетному полі парамагнетний стержень витягнеться вздовж поля, а діамагнетний – нормально до нього.
(222) Покажемо, що обертання магнетика приводить до його намагнечення (механомагнетний ефект, Барнет, 1909 р.) і, навпаки, намагнечення магнетика викликає його обертання (магнетомеханічний ефект, Айнштайн і де-Гааз, 1915 р.). Нехай діамагнетик у вигляді циліндра обертається (мал. 141). Тоді його момент імпульсу Щодо атома типу 2, то його момент імпульсу, який напрямлений до нас, зменшиться на величину моменту імпульсу тіла, що спричинить зменшення орбітального магнетного моменту, який напрямлений від нас. Але тепер спіновий магнетний момент, який напрямлений до нас, вже не скомпенсований орбітальним, тому результативний магнетний момент спрямований, як і в атома типу 1, до нас.
Для феромагнетика міркування аналогічні, з тією різницею, що роль атомів типу 1 і 2 будуть відігравати домени типу 1 і 2. Очевидно, що вільні електрони також вноситимуть свій вклад у механомагнетний ефект у магнетиках, оскільки вони внаслідок обертання тіла також обертатимуться, що спричинить виникнення магнетного моменту, пов’язаного з цим обертанням, причому напрям цього магнетного моменту буде протилежним до вектора Отже, можна зробити висновок, що внаслідок обертання всі магнетики намагнечуються в напрямі, протилежному до вектора моменту імпульсу, зв’язаного з цим обертанням (мал. 143). Якщо ж, навпаки, намагнетити магнетик, то кожен атом, отримавши додатковий магнетний момент, отримає і додатковий момент імпульсу, – виникне магнетомеханічний ефект. (223) На основі закону відсутності в природі магнетних зарядів доведемо, що на межі двох магнетиків нормальна складова вектора індукції не змінюється. Подібно до того, як ми це робили для електростатичного поля (задача 55), виділимо на межі середовищ область, обмежену нескінченно малим кубом, площа грані якого dS (мал. 144). Очевидно, що в межах цього нескінченно малого куба магнетне поле можна вважати однорідним, тому ми можемо скористатися формулою потоку однорідного поля крізь плоску поверхню. Врахувавши, що потоки через бічні взаємно протилежні грані однакові за величиною і протилежні за знаком, робимо висновок, що потік через куб – це сума потоків через верхню та нижню грані.
де З останньої рівності маємо
а для вектора
або
що означає, що в середовищі з більшою відносною магнетною проникністю нормальна складова вектора
(224) На основі теореми про магнетну циркуляцію доведемо, що на межі двох магнетиків тангенціяльна складова вектора напруженості не змінюється.
де індекси Згідно з теоремою про магнетну циркуляцію, знайдена нами циркуляція
У випадку відсутності струмів
звідки
тобто тангенціяльна складова вектора
або
тобто за умови переходу в середовище з більшою відносною магнетною проникністю тангенціяльна складова вектора
Нехай для однозначності Знайдемо відношення тангенсів кутів
тобто відношення тангенса кута падіння до тангенса кута заломлення дорівнює відношенню відповідних магнетних проникностей.
Якщо тепер через цей парамагнетик пропустити електромагнетну хвилю різних частот у напрямі магнетного поля, то поглинатися буде лише хвиля тієї частоти
Якщо ж магнетний момент атома визначається спіновим магнетним моментом (що і є насправді), то в цьому випадку важко дати класичне пояснення, бо тоді слід прийняти, що спіновий магнетний момент електрона пов'язаний з його обертанням і частота Лармора – це зміна частоти обертання самого електрона навколо своєї осі, що не має підтвердження. Більш адекватно відображає дійсність квантовий підхід, який полягає в наступному: кожен енергетичний рівень атома в магнетному полі розщеплюється на два рівні, відстань між якими визначається частотою Лармора
Тоді атом має можливість поглинати енергію електромагнетної хвилі (інакше: енергію фотона), що дорівнює цій різниці енергії. Ця енергія фотона
тому його частота
Якщо електромагнетна хвиля монохроматична, то її поглинання буде відбуватися у магнетному полі індукцією
Цю індукцію поля можна встановити експериментально, вимірюючи коефіцієнт поглинання парамагнетика за різних значень індукції магнетного поля, – за цієї індукції поля він буде максимальним. Маючи це експериментальне значення резонансного поля, можна обчислити фактор Ланде атома g.
(227) Розкриємо природу ядерного магнетного резонансу (ЯМР). Згадаємо, що ядро також може мати магнетний момент. Це ядра з непарною кількістю нуклонів. Магнетні моменти таких ядер у зовнішньому магнетному полі будуть зорієнтовані за полем, що спричинить зменшення частоти еквівалентного обертання на величину частоти Лармора. Отже, зразок може поглинати електромагнетну хвилю з частотою, рівною частоті Лармора, тобто умова ЯМР така ж, як і для ЕПР:
Очевидно, що зафіксувати ЯМР можна як і ЕПР за зміною коефіцієнта поглинання електромагнетної хвилі, проте це можна зробити і інакше: якщо припинити дію електромагнетної хвилі, то ядра почнуть випромінювати поглинуту енергію у вигляді електромагнетної хвилі, яка в соленоїді, що охоплює зразок, буде індукувати ЕРС, яку можна зафіксувати. ЯМР широко застосовують у діагностиці ракових пухлин. Тут використовують той факт, що тканини пухлин намагнечуються сильніше, ніж здорові тканини.
(228) Розкриємо природу виникнення циклотронного та магнетофононного резонансу (ЦР та МФР). Нам відомо, що вільний електрон, потрапивши в магнетне поле, починає рухатися колом навколо вектора
Якщо тепер спрямувати на зразок вздовж вектора Отже, умовою резонансу є рівність частоти фотона циклотронній частоті
З цієї рівності бачимо, що для монохроматичної хвилі резонансне поглинання буде відбуватись за певного значення індукції магнетного поля
Бачимо також, що, вимірюючи експериментально це резонансне значення магненого поля та частоту фотона, можемо знайти величину m, яка в твердому тілі не є масою вільного електрона, а так званою ефективною масою. Розглянемо природу магнетофононного резонансу (МФР). За умови, що циклотронна частота дорівнює частоті фонона, електрон поглинатиме фонона, тобто умова МФР така ж, як і ЦР з тією різницею, що замість частоти фотона є частота фонона
Зауважимо, що МФР є внутрішнім резонансом, бо фонони є в самому зразку, їх не потрібно, як фотони постачати ззовні. Тому МФР, на відміну від ЦР, можна спостерігати лише за змінами магнетоопору. З останньої формули бачимо, що за даними МФР і ЦР можна обчислити ефективну масу електрона, яка, зауважимо, є інша в кожному твердому тілі.
Поиск по сайту: |
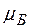 ).
).
 ).
).
 .
. до його орбітального моменту імпульсу
до його орбітального моменту імпульсу 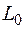 (орбітальне гіромагнетне відношення).
(орбітальне гіромагнетне відношення).
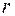 та швидкість електрона на орбіті
та швидкість електрона на орбіті  .
.
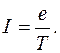

 маємо шукане відношення
маємо шукане відношення
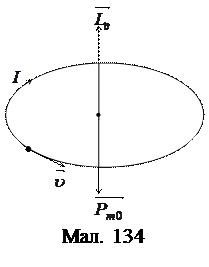 (203) Покажемо, що вектор моменту імпульсу електрона в атомі протилежний до вектора його орбітального магнетного моменту.
(203) Покажемо, що вектор моменту імпульсу електрона в атомі протилежний до вектора його орбітального магнетного моменту.
 , де
, де  – стала Планка, то і магнетний момент квантований
– стала Планка, то і магнетний момент квантований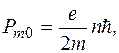
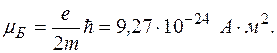
 та власний (спіновий) магнетний момент, який дорівнює магнетону Бора, знайдемо спінове гіромагнетне відношення.
та власний (спіновий) магнетний момент, який дорівнює магнетону Бора, знайдемо спінове гіромагнетне відношення.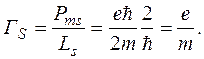
 та
та  взаємнопротилежні.
взаємнопротилежні. є меншим за магнетон Бора
є меншим за магнетон Бора  в
в  разів) то в багатьох задачах ним можна нехтувати.
разів) то в багатьох задачах ним можна нехтувати. Для електрона в атомі як момент імпульсу дорівнює векторній сумі орбітального та спінового моментів імпульсу, так і магнетний момент дорівнює векторній сумі орбітального та спінового магнетних моментів. Це означає, що гіромагнетне відношення електрона в атомі не дорівнює ні орбітальному
Для електрона в атомі як момент імпульсу дорівнює векторній сумі орбітального та спінового моментів імпульсу, так і магнетний момент дорівнює векторній сумі орбітального та спінового магнетних моментів. Це означає, що гіромагнетне відношення електрона в атомі не дорівнює ні орбітальному 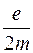 , ні спіновому
, ні спіновому  а якомусь проміжному значенню, яке залежить від кута між векторами орбітального та спінового моментів імпульсу, тобто
а якомусь проміжному значенню, яке залежить від кута між векторами орбітального та спінового моментів імпульсу, тобто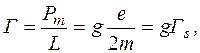

 В атомі може скластися така ситуація, що його сумарний магнетний момент дорівнюватиме нулеві (орбітальні магнетні моменти скомпенсовані спіновими). Такі речовини і є діамагнетиками. Зрозуміло, що оскільки в атомів відсутні магнетні моменти, то речовина загалом також не має магнетного моменту.
В атомі може скластися така ситуація, що його сумарний магнетний момент дорівнюватиме нулеві (орбітальні магнетні моменти скомпенсовані спіновими). Такі речовини і є діамагнетиками. Зрозуміло, що оскільки в атомів відсутні магнетні моменти, то речовина загалом також не має магнетного моменту.
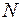 – кількість атомів у домені, тобто в одному випадку з
– кількість атомів у домені, тобто в одному випадку з 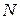 виникає флуктуація магнетного моменту, яка спричиняє виникнення домену. Представимо кількість атомів
виникає флуктуація магнетного моменту, яка спричиняє виникнення домену. Представимо кількість атомів  . Дістанемо
. Дістанемо
 співнапрямлена з його орбітальним магнетним моментом (мал. 136, (а)), і ті, для яких ця складова спрямована проти орбітального магнетного моменту, тобто за напрямом спінового магнетного моменту (мал. 136, (б)), оскільки в електрона в атомі діамагнетика орбітальний та спіновий магнетні моменти однакові й протилежні за напрямом.
співнапрямлена з його орбітальним магнетним моментом (мал. 136, (а)), і ті, для яких ця складова спрямована проти орбітального магнетного моменту, тобто за напрямом спінового магнетного моменту (мал. 136, (б)), оскільки в електрона в атомі діамагнетика орбітальний та спіновий магнетні моменти однакові й протилежні за напрямом.
 ,
, , (1)
, (1) – циклічна орбітальна частота електрона за відсутності магнетного поля.
– циклічна орбітальна частота електрона за відсутності магнетного поля. і напишемо основне рівняння динаміки в НСВ для цього випадку
і напишемо основне рівняння динаміки в НСВ для цього випадку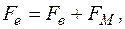
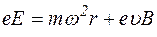 .
. (2)
(2)



 Тл дістаємо
Тл дістаємо  Гц, тоді як
Гц, тоді як  Гц, тобто
Гц, тобто 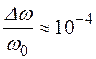 , що означає, що орбітальна частота електрона в магнетному полі змінюється на 0,01%.
, що означає, що орбітальна частота електрона в магнетному полі змінюється на 0,01%.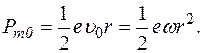
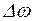 він зміниться на величину
він зміниться на величину
 дістанемо зміну орбітального моменту електрона в магнетному полі.
дістанемо зміну орбітального моменту електрона в магнетному полі.
 .
.
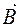 дорівнює сумі індукції зовнішнього
дорівнює сумі індукції зовнішнього  та внутрішнього
та внутрішнього  магнетних полів.
магнетних полів. (1)
(1)

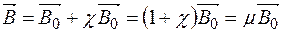 ,
,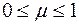 , магнетне поле послаблюється, а в пара- та феромагнетиках, оскільки
, магнетне поле послаблюється, а в пара- та феромагнетиках, оскільки 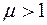 , – підсилюється, причому у феромагнетиках, для яких
, – підсилюється, причому у феромагнетиках, для яких  , в кілька порядків, разів.
, в кілька порядків, разів.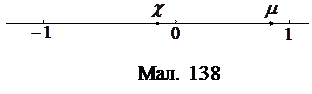 Нам відомо, що діамагнетики намагнечуються проти зовнішнього магнетного поля (задача 211), тобто вектор
Нам відомо, що діамагнетики намагнечуються проти зовнішнього магнетного поля (задача 211), тобто вектор  є протилежним до вектора
є протилежним до вектора  , а оскільки
, а оскільки  , то
, то  . Крім того, відомо, що цей ефект дуже слабкий (задача 213) тобто вектор
. Крім того, відомо, що цей ефект дуже слабкий (задача 213) тобто вектор  за своєю величиною значно менший за
за своєю величиною значно менший за  . Число
. Число  справа від нуля і близько до 1 (мал. 138).
справа від нуля і близько до 1 (мал. 138). і, відповідно,
і, відповідно,  .
. .
. (чи індукції магнетного поля в магнетику В від індукції зовнішнього магнетного поля
(чи індукції магнетного поля в магнетику В від індукції зовнішнього магнетного поля  ).
). Отже, для феромагнетика
Отже, для феромагнетика ,
, ,
, ), якщо
), якщо  то
то  . На перший погляд видається, що тоді
. На перший погляд видається, що тоді  , тобто
, тобто 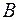 зростає пропорційно до
зростає пропорційно до  чи
чи  цим зростанням можна знехтувати і вважати, що практично
цим зростанням можна знехтувати і вважати, що практично  .
. , то феромагнетик залишиться постійним магнетом. Для того, щоб повернутися в точку 0, слід до феромагнетика прикласти зовнішнє поле протилежного напряму до поля в ньому, яке створить поле всередині феромагнетика такої ж величини і тоді виключити зовнішнє поле.
, то феромагнетик залишиться постійним магнетом. Для того, щоб повернутися в точку 0, слід до феромагнетика прикласти зовнішнє поле протилежного напряму до поля в ньому, яке створить поле всередині феромагнетика такої ж величини і тоді виключити зовнішнє поле. Раніше ми вже показали (задача 155), що магнетний диполь (коловий струм), як і електричний, в неоднорідному магнетному полі рухається в бік сильнішого поля. Оскільки парамагнетик і є системою замкнених мікрострумів, то на них діє сила в бік сильнішого поля, що і виявляє себе, як дія на весь парамагнетик.
Раніше ми вже показали (задача 155), що магнетний диполь (коловий струм), як і електричний, в неоднорідному магнетному полі рухається в бік сильнішого поля. Оскільки парамагнетик і є системою замкнених мікрострумів, то на них діє сила в бік сильнішого поля, що і виявляє себе, як дія на весь парамагнетик. Щодо діамагнетика, то він, як відомо, намагнечується проти зовнішнього магнетного поля, а це можна трактувати, як появу замкнених струмів (мал. 140) площини яких є нормальними до зовнішнього магнетного поля, причому напрями цих струмів такі, що їхні магнетні моменти спрямовані проти цього поля. З малюнка видно, що сила Ампера
Щодо діамагнетика, то він, як відомо, намагнечується проти зовнішнього магнетного поля, а це можна трактувати, як появу замкнених струмів (мал. 140) площини яких є нормальними до зовнішнього магнетного поля, причому напрями цих струмів такі, що їхні магнетні моменти спрямовані проти цього поля. З малюнка видно, що сила Ампера 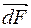 , яка діє на елемент струму в області сильнішого поля напрямлена в область слабшого поля і вона є більшою за ту ж силу, яка діє на елемент струму в області слабшого поля, тому рівнодійна цих сил спрямована в область слабшого поля, тобто діамагнетик виштовхується з магнетного поля.
, яка діє на елемент струму в області сильнішого поля напрямлена в область слабшого поля і вона є більшою за ту ж силу, яка діє на елемент струму в області слабшого поля, тому рівнодійна цих сил спрямована в область слабшого поля, тобто діамагнетик виштовхується з магнетного поля. спрямований в площину малюнка. Усі атоми цього тіла можна поділити на дві групи: 1) ті, у яких вектор їхнього орбітального моменту імпульсу проектується на напрям
спрямований в площину малюнка. Усі атоми цього тіла можна поділити на дві групи: 1) ті, у яких вектор їхнього орбітального моменту імпульсу проектується на напрям  Покажемо, що як в перших, так і в других атомів з’явиться магнетний момент, причому однакового напряму. Дійсно, момент імпульсу атома
Покажемо, що як в перших, так і в других атомів з’явиться магнетний момент, причому однакового напряму. Дійсно, момент імпульсу атома  збільшиться на величину моменту імпульсу тіла, що спричинить збільшення його орбітального магнетного моменту, оскільки вони пов’язані гіромагнетним відношенням (задача 202). Як видно з малюнка цей сумарний момент імпульсу спрямований в площину малюнка, тому орбітальний магнетний момент – з площини малюнка. Але оскільки він збільшився, то він вже не є скомпенсований спіновим магнетним моментом (пам’ятаємо, що йдеться про діамагнетик) і результативний магнетний момент вже не дорівнює нулеві і має напрям з площини малюнка.
збільшиться на величину моменту імпульсу тіла, що спричинить збільшення його орбітального магнетного моменту, оскільки вони пов’язані гіромагнетним відношенням (задача 202). Як видно з малюнка цей сумарний момент імпульсу спрямований в площину малюнка, тому орбітальний магнетний момент – з площини малюнка. Але оскільки він збільшився, то він вже не є скомпенсований спіновим магнетним моментом (пам’ятаємо, що йдеться про діамагнетик) і результативний магнетний момент вже не дорівнює нулеві і має напрям з площини малюнка. Розглянемо тепер парамагнетний циліндр. Парамагнетизм означає наявність в атомів магнетних моментів. Якщо циліндр у стані спокою (мал. 142), то магнетні моменти атомів типу 1 і 2 є взаємно протилежними (нехай магнетний момент атома визначається орбітальним магнетним моментом). Коли циліндр обертається, то в атома типу 1 внаслідок зростання моменту імпульсу, зростає і орбітальний магнетний момент, який спрямований проти моменту імпульсу (на мал. 142 до нас). Водночас в атома типу 2 момент імпульсу зменшується тому зменшується і магнетний момент, який спрямований від нас. У результаті сумарний магнетний момент атомів 1 і 2 вже не дорівнює нулеві, а має певну величину й напрям до нас, тобто проти вектора моменту імпульсу, викликаного обертанням парамагнетика.
Розглянемо тепер парамагнетний циліндр. Парамагнетизм означає наявність в атомів магнетних моментів. Якщо циліндр у стані спокою (мал. 142), то магнетні моменти атомів типу 1 і 2 є взаємно протилежними (нехай магнетний момент атома визначається орбітальним магнетним моментом). Коли циліндр обертається, то в атома типу 1 внаслідок зростання моменту імпульсу, зростає і орбітальний магнетний момент, який спрямований проти моменту імпульсу (на мал. 142 до нас). Водночас в атома типу 2 момент імпульсу зменшується тому зменшується і магнетний момент, який спрямований від нас. У результаті сумарний магнетний момент атомів 1 і 2 вже не дорівнює нулеві, а має певну величину й напрям до нас, тобто проти вектора моменту імпульсу, викликаного обертанням парамагнетика. . З мал. 141 та 142 також видно, що пов’язані з обертанням тіла магнетні моменти ядер послаблюють механомагнетний ефект.
. З мал. 141 та 142 також видно, що пов’язані з обертанням тіла магнетні моменти ядер послаблюють механомагнетний ефект. За теоремою Остроградського-Гауса для магнетного поля
За теоремою Остроградського-Гауса для магнетного поля ,
,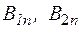 – нормальні до межі середовищ складові вектора
– нормальні до межі середовищ складові вектора 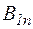 тому, що кут між вектором
тому, що кут між вектором  і вектором зовнішньої нормалі в першому середовищі тупий і косинус цього кута відповідно від’ємний).
і вектором зовнішньої нормалі в першому середовищі тупий і косинус цього кута відповідно від’ємний).
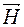
 ,
,
 Подібно до того як ми це робили для електростатичного поля (задача 54) побудуємо на межі магнетиків прямокутний замкнений контур зі сторонами
Подібно до того як ми це робили для електростатичного поля (задача 54) побудуємо на межі магнетиків прямокутний замкнений контур зі сторонами 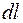 i
i  (мал. 145). Оскільки поле в межах цього нескінченно малого контура однорідне, то циркуляція вектора
(мал. 145). Оскільки поле в межах цього нескінченно малого контура однорідне, то циркуляція вектора  вздовж будь-якої сторони контура є добутком проекції вектора
вздовж будь-якої сторони контура є добутком проекції вектора 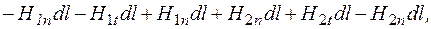
 i
i  означають нормальну й тангенціяльну до межі середовищ складову вектора
означають нормальну й тангенціяльну до межі середовищ складову вектора 
 дорівнює струму, який пронизує поверхню, обмежену цим контуром, тобто
дорівнює струму, який пронизує поверхню, обмежену цим контуром, тобто
 ,
, ,
, ,
, ,
, (225) Виведемо закон заломлення силових ліній на межі двох магнетиків.
(225) Виведемо закон заломлення силових ліній на межі двох магнетиків. Оскільки нормальна складова вектора
Оскільки нормальна складова вектора 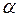 і
і  .
.
 (226) Розкриємо природу виникнення електронного парамагнетного резонансу (ЕПР).
(226) Розкриємо природу виникнення електронного парамагнетного резонансу (ЕПР). Якщо помістити парамагнетик у магнетне поле, то магнетні моменти атомів будуть зорієнтовані за напрямом поля (задача 151). Якщо магнетний момент атома визначається орбітальним магнетним моментом (сумарний орбітальний магнетний момент більший за сумарний спіновий), то в магнетному полі орбітальна частота, яка пов’язана з магнетним моментом, зменшується. Дійсно, додаткова сила з боку зовнішнього магнетного поля спричиняє сходження електрона зі своєї орбіти (мал. 147), що надалі зумовлює виникнення сили
Якщо помістити парамагнетик у магнетне поле, то магнетні моменти атомів будуть зорієнтовані за напрямом поля (задача 151). Якщо магнетний момент атома визначається орбітальним магнетним моментом (сумарний орбітальний магнетний момент більший за сумарний спіновий), то в магнетному полі орбітальна частота, яка пов’язана з магнетним моментом, зменшується. Дійсно, додаткова сила з боку зовнішнього магнетного поля спричиняє сходження електрона зі своєї орбіти (мал. 147), що надалі зумовлює виникнення сили  , яка дорівнює частоті Лармора
, яка дорівнює частоті Лармора  , або
, або








