 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 5. Електромагнетна індукція
Фізичні явища · Електромагнетна індукція – це явище виникнення ЕРС в замкненому контурі, який обмежує поверхню, що пронизується змінним магнетним потоком. · Самоіндукція – явище виникнення ЕРС в замкненому провідному контурі внаслідок зміни сили струму в цьому ж контурі. · Взаємоіндукція – явище виникнення ЕРС в провіднику внаслідок зміни сили струму в іншому провіднику. · Скін-ефект – це явище тенденції протікання змінного струму ближче до поверхні провідника.
Фізичні поняття · Вихрові струми (струми Фуко) – струми, які виникають у провідниках недротоподібної форми внаслідок явища електромагнетної індукції.
Фізичні величини · Індуктивність провідника – це відношення магнетного потоку через поверхню, обмежену провідником, до сили струму в провіднику, що спричинив цей магнетний потік (позначення L)
Фізичні системи й прилади · Флюксометр – маленький плоский соленоїд (діаметром приблизно 1см) приєднаний до гальванометра. Прилад призначений для вимірювання індукції магнетного поля.
Постулати Ø Закон електромагнетної індукції (Фарадея): якщо магнетний потік, крізь поверхню, яка обмежена замкненим провідним контуром, змінюється у часі, то в цьому контурі виникає ЕРС, що дорівнює темпу зміни цього магнетного потоку, причому індукований в контурі струм має такий напрям, що створений ним магнетний потік прагне компенсувати ту зміну магнетного потоку, яка його спричинила.
Ø Закон електромагнетної індукції (Максвелла): змінне магнетне поле спричиняє виникнення вихрового електричного поля, циркуляція напруженості якого вздовж будь-якого замкненого контура (уявного чи реального) дорівнює темпу зміни магнетного потоку крізь довільну поверхню, що обмежена цим контуром.
Задачі (187) Перевіримо закон електромагнетної індукції Фарадея для відрізка проводу, який рухається в однорідному магнетному полі нормально до його силових ліній. Перевірка закону електромагнетної індукції в цьому випадку зводиться до того, що слід показати, що в проводі виникне ЕРС, яка дорівнює темпу зміни магнетного потоку. Як тільки провід почне рухатися в магнетному полі з певною швидкістю
або
а для модулів цих векторів
звідки
або
Зазначимо, що оскільки процес розділення зарядів у проводі безперервний то різниця потенціялів між його кінцями є насправді електрорушійною силою, тобто
Представивши далі швидкість
Застосувавши означення ЕРС та магнетного потоку, останню рівність можемо представити
(188) З’ясуємо, у чому полягає різниця між формулюваннями закону електромагнетної індукції Фарадея та Максвелла. Закон електромагнетної індукції Фарадея передбачає існування провідного контура, у якому має виникнути струм внаслідок виникнення в ньому ЕРС індукції, тоді як це й же закон у формулюванні Максвелла стверджує, що наявність провідного контура не обов’язкова, вихрове електричне поле виникає незалежно від його існування, а цими контурами є замкнені силові лінії вихрового електричного поля.
(189) На основі закону електромагнетної індукції Фарадея та означення магнетного потоку проаналізуємо способи, якими можна отримати ЕРС індукції. Згідно з законом електромагнетної індукції та означенням магнетного потоку для випадку однорідного (не обов’язково стаціонарного) магнетного поля
де S – площа обмежена контуром, З останньої формули бачимо, що є принаймні три способи отримання ЕРС: 1) змінювати в часі індукцію магнетного поля 2) змінювати площу S,обмежену контуром, 3) змінювати кут Найбільш практичним є третій спосіб. Саме принцип обертання контура в магнетному полі міститься в основі роботи генераторів змінної ЕРС, які генерують електричний струм на теплових, водних, атомних, вітрових та припливних електростанціях, і забезпечують на нинішній день основну частку електроенергії, яку споживає людство.
(190). Знайдено напрям індукованого струму у таких випадках електромагнетної індукції: а) провідний коловий контур є в однорідному магнетному полі, індукція якого зменшусться(мал. 127, (а)); б) провідний коловий контур деформують в постійному однорідному магнетному полі(мал. 127, (б)); в) провідний контур рівномірно обертається в постійному однорідному магнетному полі(мал. 127, (в)).
а) Внаслідок зміни магнетного потоку через поверхню, обмежену контуром у ньому виникає ЕРС згідно з законом електромагнетної індукції. Струм, який потече в ньому, має два можливі напрями – за годинниковою стрілкою чи проти. Припустимо, що він тече за годинниковою стрілкою. Тоді створене ним магнетне поле в області, обмеженій контуром, буде співнапрямлене з зовнішнім полем, яке спричинило цей струм, тобто магнетний потік індукованого струму підтримуватиме магнетний потік зовнішнього поля, компенсуючи його від’ємну зміну, що цілком відповідає закону електромагнетної індукції. Отже, напрям індуктивного струму вибрано правильно. Очевидно, якщо б зовнішнє магнетне поле зростало, то струм потік би в протилежному напрямі. Зазначимо, що ту частину закону електромагнетної індукції Фарадея, яка говорить про напрям індукованого струму, називають правилом Ленца.
б) Оскільки площа контура зменшується, то магнетний потік крізь поверхню, обмежену ним, також зменшується і зміна магнетного потоку від’ємна (наступне значення магнетного потоку є меншим за попереднє). Згідно з правилом Ленца, магнетний потік ін.дукованого струму повинен компенсувати цю від’ємну зміну магнетного потоку, тобто магнетне поле індукованого струму повинно бути співнапрямлене із зовнішнім магнетним полем, а для цього струм, згідно з Законом Біо-Саваро-Лапласа, має текти за годинниковою стрілкою. в) За обертання контура в магнетному полі (мал. 127, (б)) за першу чверть періоду обертання магнетний потік буде зменшуватися внаслідок збільшення кута між вектором індукції та вектором нормалі до площини контура. При цьому, очевидно, індукований струм потече за годинниковою стрілкою, тобто так, щоб його магнетний потік підтримував магнетний потік зовнішнього поля (або інакше кажучи протидіяв від’ємній зміні магнетного потоку зовнішнього поля). У другій чверті періоду обертання контура магнетний потік знову зростатиме і струм потече в протилежній бік, тобто проти годинникової стрілки, компенсуючи, згідно з правилом Ленца, додатну зміну магнетного потоку. У наступних чвертях періоду струм знову змінюватиме свій напрям.
(191) Пояснимо, як вимірюють індукцію магнетного поля флюксометром.
Унаслідок проходження цього заряду стрілка гальванометра відхилиться на кут
де b – коефіцієнт пропорційності між З останньої формули видно, що кут відхилення стрілки гальванометра пропорційний до індукції магнетного поля з коефіцієнтом пропорційності а, який називають сталою флюксометра (коефіцієнт пропорційності b називають сталою гальванометра). Сталу флюксометра знаходять експериментально, вимірявши кут З останньої формули також видно, що, знаючи сталу флюксометра, шкалу гальванометра можна проградуювати в одиницях індукції магнетного поля, тобто в теслах.
(192) Пояснимо механізм виникнення вихрових струмів (струмів Фуко).
Вихрові струми є шкідливими в осердях електромагнетів та трансформаторів. Щоб їх зменшити, ці осердя роблять не з суцільного куска сталі, а з пластин, розміщених паралельно до магнетного поля і склеєних між собою діелектриком. Вихрові струми використовують у роторах асинхронних електродвигунів та в індукційних печах для нагрівання чи плавлення металів, а також у фізіотерапії для нагрівання органів та тканин людей (індуктотермія).
(193) Пояснимо механізм виникнення скін-ефекту.
Коли струм в провіднику спадає (мал. 130, б), вихрові струми потечуть так, що підсилюватимуть струм всередині, тобто не даватимуть йому спадати і послаблюватимуть по краях, тобто сприятимуть його спаданню. Отже, як у випадку зростання струму, так і у випадку його спадання, опір провідника буде більшим всередині і меншим по його краях. Очевидно, що цей ефект буде більшим, що більша буде частота зміни струму (бо тоді більшим буде темп зміни магнетного поля і, відповідно, більшими вихрові струми).
(194) Пояснимо природу явища самоіндукції і встановимо вираз для ЕРС самоіндукції. Уявимо собі замкнений контур (чи соленоїд), у якому тече змінний струм. Оскільки струм змінюється з часом, то поверхня, обмежена цим контуром, пронизується змінним магнетним потоком, що спричиняє виникнення ЕРС і, як наслідок, струму. Цей новий струм залежить не від величини струму, який тече в контурі, а від темпу його зміни. Дійсно, магнетний потік крізь поверхню, обмежену контуром, пропорційний до індукції поля струму, яке, своєю чергою, пропорційне до сили струму.
тобто
Коефіцієнт пропорційності між цими величинами позначають буквою L і називають індуктивністю, тобто
Згідно з законом електромагнетної індукції
(195) Представимо закон електромагнетної індукції у диференціяльній формі. Виходимо з інтегральної форми закону електромагнетної індукції:
Циркуляцію, у лівій частині цієї рівності, представимо згідно з теоремою Стокса, яка стверджує, що циркуляція якогось вектора вздовж будь-якого замкненого контура дорівнює потоку ротора цього вектора крізь будь-яку поверхню, яка спирається на цей контур, тобто
Переставивши місцями операції інтегрування та диферентціювання в правій частині цієї рівності, маємо
Оскільки тепер обидва інтеграли – це інтеграли за однією і тією ж поверхнею S, то їхня рівність означає рівність підінтегральних виразів, а саме
Ми отримали диференціяльну форму закону електромагнетної індукції.
(196) Знайдемо вираз для індуктивності нормального соленоїда, тобто виразимо цю величину через геометричні розміри соленоїда та густоту витків. Згідно з означенням, індуктивність – це відношення магнетного потоку до сили струму, яка є причиною цього магнетного потоку, тому
де ми, крім означення індуктивності, застосували послідовно означення магнетного потоку, формулу магнетної індукції нормального соленоїда, та означення густоти витків нормального соленоїда.
(197) Розкриємо принцип роботи прискорювача заряджених частинок бетатрона та встановимо умову, за якої заряджена частинка буде утримуватися в бетатроні на сталій орбіті. У бетатроні заряджені частинки прискорюються у порожнистому відпомпованому тороїді, який поміщений в неоднорідне і змінне в часі магнетне поле, що слабшає від центру до країв (мал. 131). Неоднорідність магнетного поля забезпечується зрізанням країв полюсів електромагнета.
Покажемо, що для того, щоб заряджені частинки оберталися на сталій орбіті, магнетне поле дійсно має бути неоднорідним, і встановимо наскільки. Очевидно, що для сталого обертання частинки відцентрова сила інерції має компенсуватись силою магнетного поля, яка виникне, як тільки вона почне рухатись, тобто
звідки
де Продиференціюємо останню рівність за часом
Згідно з основним рівнянням динаміки
тому
звідки
де Е – напруженість прискорювального вихрового електричного поля, яку знайдемо із закону електромагнетної індукції
Інтеграл зліва дорівнює EL, де L – довжина кола, а справа
звідки
Підставивши отриманий вираз для Е у формулу (1), дістанемо
Звідки
що означає, що для забезпечення стабільності орбіти зарядженої частинки індукція магнетного поля в області орбіти частинки має дорівнювати половині середнього значення магнетного поля по області, обмеженій цією орбітою. Зверніть увагу також на те, що для того, щоб прискорювати негативно заряджені частинки, магнетне поле має бути спадним, бо при цьому сила з боку магнетного поля буде протидіяти відцентрованій силі. Для прискорення позитивних частинок, навпаки, магнетне поле має зростати.
(198)Установимо закон спадання сили струму після розмикання кола постійного струму.
Згідно з другим правилом Кірхгофа, яке, очевидно, можна застосовувати не тільки до постійного струму, а й до будь-якого миттєвого значення змінного струму
де IR – напруга в колі. Розв’язок останнього диференціяльного рівняння
де С – стала, яку знаходимо з умови, що в початковий момент часу t=0, тобто в момент розмикання кола, сила струму мала певне початкове значення
або врахувавши закон Ома для замкненого кола
Як бачимо, темп падіння сили струму залежить від параметрів кола R i L – зі збільшенням R сила струму спадає швидше, а зі збільшення L – повільніше. Зауважимо, що як опір R, так і індуктивність L, не обов’язково мають бути відокремленими в якомусь елементі кола, а можуть бути розподілені по колі.
(199)Установимо закон зростання сили струму після замикання кола постійного струму. Після замикання кола постійного струму (мал. 133), як і після його вимикання (задача 198), виникне ЕРС самоіндукції, і тому в колі буде дві ЕРС – ЕРС самоіндукції та ЕРС джерела. Згідно з другим правилом Кірхгофа
або
Розв’язок цього неоднорідного диференціяльного рівняння першого порядку складається з розв’язку відповідного однорідного рівняння та свого частинного розв’язку. Частинний розв’язок цього рівняння знаходиться легко, бо шукаємо його як сталу величину для якої, очевидно,
Підставивши початкові умови, а саме t=0 та I=0, визначивши за цих умов
дістанемо
(200)Виразимо енергію магнетного поля через силу струму, який є джерелом цього поля. Енергію магнетного поля будемо шукати, як роботу сторонніх сил, яку вони виконують, щоб подолати ЕРС самоіндукції, яка виникає при вмиканні джерела постійної ЕРС. За означенням потужності елементарна робота
де P – потужність джерела ЕРС самоіндукції. Підставивши в цей вираз
Отже, енергія магнетного поля створеного струмом I
(201)Виразимо густину енергії магнетного поля через індукцію цього поля. Зробимо це для поля нормального соленоїда. В останній вираз для енергії магнетного поля підставимо вираз для індуктивності нормального соленоїда і отримаємо з цієї формули вираз для енергії магнетного поля цього соленоїда.
звідки, поділивши ліву й праву частину цієї рівності на об’єм соленоїда V, дістанемо густину енергії магнетного поля
або
Оскільки вектори
Поиск по сайту: |

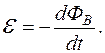

 (мал. 126), то з боку цього поля на електрони почне діяти сила
(мал. 126), то з боку цього поля на електрони почне діяти сила 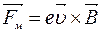 ,напрям якої, згідно з правилом правого гвинта, буде вниз, що спричинить рух електронів до цього кінця проводу. Цей рух, своєю чергою, призведе до порушення електронейтральності в проводі і, як наслідок, до виникнення електричного поля, спрямованого від верхнього кінця проводу до нижнього. Коли напруженість електричного поля зросте до такої величини, що його сила
,напрям якої, згідно з правилом правого гвинта, буде вниз, що спричинить рух електронів до цього кінця проводу. Цей рух, своєю чергою, призведе до порушення електронейтральності в проводі і, як наслідок, до виникнення електричного поля, спрямованого від верхнього кінця проводу до нижнього. Коли напруженість електричного поля зросте до такої величини, що його сила  зрівняється з силою магнетного поля, рух електронів до нижнього кінця проводу припиниться.
зрівняється з силою магнетного поля, рух електронів до нижнього кінця проводу припиниться.
 Умова цього стану
Умова цього стану




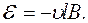
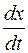 і внісши під знак похідної сталі
і внісши під знак похідної сталі  і B, дістанемо
і B, дістанемо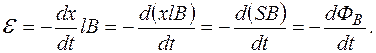

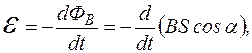
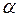 – кут між вектором індукції магнетного поля
– кут між вектором індукції магнетного поля 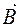 та нормаллю до цієї поверхні
та нормаллю до цієї поверхні 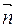 .
.
 Помістимо плоский соленоїд флюксометра, який має N витків, в ту область магнетного поля, де ми хочемо виміряти його індукцію нормально до його силових ліній, тобто так, щоб магнетний потік через нього був максимальним (мал. 128). Далі слід зробити так, щоб магнетний потік зменшився до нуля. Це, очевидно, можна зробити, виключивши струм, який створює це поле, або повернувши соленоїд на 900. При цьому внаслідок електромагнетної індукції через гальванометр пройде заряд
Помістимо плоский соленоїд флюксометра, який має N витків, в ту область магнетного поля, де ми хочемо виміряти його індукцію нормально до його силових ліній, тобто так, щоб магнетний потік через нього був максимальним (мал. 128). Далі слід зробити так, щоб магнетний потік зменшився до нуля. Це, очевидно, можна зробити, виключивши струм, який створює це поле, або повернувши соленоїд на 900. При цьому внаслідок електромагнетної індукції через гальванометр пройде заряд
 , який пропорційний до цього заряду, тобто
, який пропорційний до цього заряду, тобто
 і q,
і q,  – коефіцієнт пропорційності між
– коефіцієнт пропорційності між 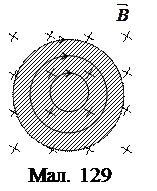 Розглянемо металеву пластину в магнетному полі (мал. 129). Нехай магнетний потік крізь цю пластину змінюється в часі. Тоді в кожному уявному контурі цієї пластини, згідно з законом електромагнетної індукції, виникає ЕРС, а оскільки ці контури провідні, то в них виникають струми, які будуть себе виявляти передовсім нагріванням пластини. Крім того, якщо пластина була нерухома (зміна магнетного потоку забезпечується, наприклад, зміною індукції магнетного поля), то вона може почати рухатися під дією сил Ампера, які почнуть діяти на вихрові струми з боку магнетного поля. Якщо ж зміна магнетного потоку забезпечується, наприклад, обертанням пластини в магнетному полі, то вона буде гальмуватись і т.п, тобто крім ефекту нагрівання можуть виникати різні механічні ефекти, пов’язані з дією магнетного поля на вихрові струми. Якщо в пластині зробити прорізи, наприклад, у радіальному напрямі, то вихрових струмів буде значно менше.
Розглянемо металеву пластину в магнетному полі (мал. 129). Нехай магнетний потік крізь цю пластину змінюється в часі. Тоді в кожному уявному контурі цієї пластини, згідно з законом електромагнетної індукції, виникає ЕРС, а оскільки ці контури провідні, то в них виникають струми, які будуть себе виявляти передовсім нагріванням пластини. Крім того, якщо пластина була нерухома (зміна магнетного потоку забезпечується, наприклад, зміною індукції магнетного поля), то вона може почати рухатися під дією сил Ампера, які почнуть діяти на вихрові струми з боку магнетного поля. Якщо ж зміна магнетного потоку забезпечується, наприклад, обертанням пластини в магнетному полі, то вона буде гальмуватись і т.п, тобто крім ефекту нагрівання можуть виникати різні механічні ефекти, пов’язані з дією магнетного поля на вихрові струми. Якщо в пластині зробити прорізи, наприклад, у радіальному напрямі, то вихрових струмів буде значно менше. Розглянемо змінний в часі струм, який тече в провіднику, і в якийсь момент часу він для прикладу, зростає (мал. 130, а). Тоді зростає і магнетне поле цього струму. Це зростаюче магнетне поле спричиняє до виникнення ЕРС в будь-якому контурі, що пронизується цим магнетним полем (контури А і В). Згідно з правилом Ленца, індукований струм потече так, що він підсилюватиме струм по краях і послаблюватиме його всередині.
Розглянемо змінний в часі струм, який тече в провіднику, і в якийсь момент часу він для прикладу, зростає (мал. 130, а). Тоді зростає і магнетне поле цього струму. Це зростаюче магнетне поле спричиняє до виникнення ЕРС в будь-якому контурі, що пронизується цим магнетним полем (контури А і В). Згідно з правилом Ленца, індукований струм потече так, що він підсилюватиме струм по краях і послаблюватиме його всередині.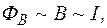





 замінимо на
замінимо на  . Дістанемо
. Дістанемо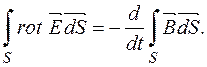



 Змінне магнетне поле, згідно з законом електромагнетної ін.дукції, спричиняє виникнення вихрового електричного поля, лінії напруженості якого замкнені й нормальні до силових ліній магнетного поля. Одна з таких силових ліній у випадку спадання магнетного поля показана на мал. 131. Це вихрове електричне поле і прискорює заряджені частинки.
Змінне магнетне поле, згідно з законом електромагнетної ін.дукції, спричиняє виникнення вихрового електричного поля, лінії напруженості якого замкнені й нормальні до силових ліній магнетного поля. Одна з таких силових ліній у випадку спадання магнетного поля показана на мал. 131. Це вихрове електричне поле і прискорює заряджені частинки.

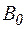 – індукція магнетного поля в області тороїда, r – радіус тороїда.
– індукція магнетного поля в області тороїда, r – радіус тороїда.
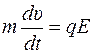

 (1)
(1)
 , де
, де 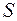 – площа круга, а
– площа круга, а  – середнє значення індукції магнетного поля в межах цього круга, тобто неоднорідне поле ми уявно замінили на однорідне, яке створює такий самий потік і має індукцію
– середнє значення індукції магнетного поля в межах цього круга, тобто неоднорідне поле ми уявно замінили на однорідне, яке створює такий самий потік і має індукцію  . Отже, остання рівність виглядає так:
. Отже, остання рівність виглядає так:



 Якщо розімкнути коло постійного струму, то струм, спадаючи, спричинить виникнення ЕРС самоіндукції вираз якої
Якщо розімкнути коло постійного струму, то струм, спадаючи, спричинить виникнення ЕРС самоіндукції вираз якої  де L – індуктивність кола (мал. 132).
де L – індуктивність кола (мал. 132).
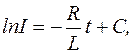
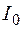 . Підставивши ці значення в розв’язок, дістанемо
. Підставивши ці значення в розв’язок, дістанемо  і остаточний розв’язок
і остаточний розв’язок




 . З цієї умови з останнього рівняння частинний розв’язок – це стала
. З цієї умови з останнього рівняння частинний розв’язок – це стала  Отже, загальний розв’язок
Отже, загальний розв’язок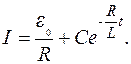

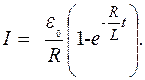
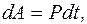
 і враховуючи, що
і враховуючи, що  дістанемо
дістанемо


 ,
,

 співнапрямлені, то
співнапрямлені, то