 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема1. Закон Ампера. Індукція магнетного поля. Провідник зі струмом у магнетному поліСтр 1 из 10Следующая ⇒
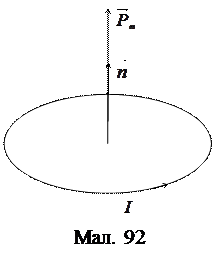
Розділ ІІІ. Магнетне поле Фізичні поняття · Магнетне поле − це субстанція, яка створюється електричними струмами й виявляє себе за дією на електричний струм. · Елемент струму − це добуток сили струму I на елемент довжини провідника · Сила Ампера − це сила, яка діє з боку магнетного поля на провідник зі струмом. · Силова лінія магнетного поля − це лінія, вздовж якої вистрояться дуже малі магнетні стрілки, якщо ними щільно заповнити простір, де є магнетне поле (інакше кажучи, це лінія, у кожній точці якої вектор магнетної індукції є дотичним до цієї лінії).
Фізичні величини ·Індукція магнетного поля − це вектор
де ·Магнетний момент замкненого струму – це вектор
де
Фізичні системи й прилади · Магнетна стрілка − це стрілка з магнетним моментом, спрямованим уздовж неї.
Постулати Ø Закон Ампера: сила, з якою магнетне поле з індукцією
Закон Ампера водночас є означенням індукції магнетного поля (так як другий закон Ньютона є означенням сили). Очевидно, що як і будь-який постулат, закон Ампера встановлений експериментально.
Задачі
(150) Знайдемо метод обчислення сили, яка діє з боку магнетного поля на провідник зі струмом довільної форми. Закон Ампера дає нам можливість обчислити силу, яка діє з боку поля лише на один елемент струму, тобто силу
(151) Установимо, як зорієнтується вільний контур зі струмом в однорідному магнетному полі.
Сили, які діють на дві сторони, паралельні до променя зору створюють обертальний момент. Тому контур буде обертатися проти годинникової стрілки, доки його площина не стане нормальною до ліній індукції і, відповідно, вектор магнетного моменту Отже, підсумовуючи, можна стверджувати, що як би не був початково розміщений вільний контур зі струмом в однорідному магнетному полі, він повернеться так, що його магнетний момент буде співнапрямленим з вектором магнетної індукції. Крім того, з мал. 94 (а) і закону Ампера випливає, що момент сил, який повертає контур, є найбільшим тоді, коли площина контура паралельна до вектора індукції (магнетний момент контура нормальний до вектора індукції).
(152) Знайдемо вираз для моменту сили, який обертає коловий контур зі струмом у випадку, коли площина контура паралельна до ліній магнетної індукції.
Ця елементарна сила створює момент
Додавши всі елементарні моменти, дістанемо момент, який повертає контур
де Від інтегрування за довжиною перейдемо до інтегрування за кутом
Оскільки вектор моменту сили
або врахувавши означення магнетного моменту
(153) Знайдемо силу, яка розтягає (стискає) коловий контур зі струмом, магнетний момент якого паралельний (антипаралельний) до вектора індукції однорідного магнетного поля.
На мал. 96 показана ця ситуація так, що вектор індукції нормальний до площини малюнка. Бачимо, що в кожній точці контура сила Ампера спрямована вздовж радіуса назовні, тобто вона розтягає його. Величина цієї сили розрахована на одиницю довжини, згідно з законом Ампера
Оскільки кут
Сила натягу яка розтягує кільце в будь-якій його точці (в точці А) – це проекція всіх сил Ампера прикладених до півкільця, на вісь нормальну до напряму АВ.
(154) Покажемо, що можливий стан рівноваги контура зі струмом за антипаралельного напряму його магнетного моменту щодо напряму зовнішнього однорідного магнетного поля, проте, цей стан рівноваги не є стійким.
Дійсно, якщо розмістити контур так, що його магнетний момент буде антипаралельним до вектора індукції (
(155) Покажемо, що в неоднорідному магнетному полі контур зі струмом не набуде стану спокою, а буде переміщуватися в область сильнішого поля.
Ця поведінка контура зі струмом в неоднорідному магнетному полі нагадує нам поведінку диполя в неоднорідному електричному полі (розділ 1, задача 16).
(156) Знайдемо вираз для величини орбітального магнетного моменту електрона в атомі. Справді, орбітальний рух електрона в атомі можна трактувати як струм, тому цей рух створює магнетний момент, величина якого
Згідно з означенням сили струму, в цьому випадку
де T − період обертання електрона навколо ядра (за час T через поперечний переріз уявного провідника проходить заряд, який дорівнює заряду електрона). З останніх двох формул та формули зв’язку між періодом та циклічною частотою дістанемо
або на основі формули зв’язку між кутовою та лінійною швидкостями
де
(157) Установимо вираз для магнетного моменту рівномірно зарядженого зарядом Кожен елементарний струм
Оскільки цей струм
де T − період обертання стержня, Тепер елементарний магнетний момент
і повний магнетний момент
де замість Незаряджений стержень, навіть металевий, не створює при обертанні магнетного моменту, хоча, на перший погляд, видається, що струм, створений упорядкованим рухом електронів, мав би спричинювати магнетний момент. Проте цей струм є скомпенсований таким же за величиною і протилежно спрямованим струмом позитивних йонів.
Поиск по сайту: |
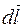 .
. , модуль якого
, модуль якого
 – модуль сили, з якою магнетне поле діє на елемент струму
– модуль сили, з якою магнетне поле діє на елемент струму 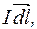
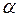 – кут між векторами
– кут між векторами  і
і 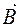 , а напрям вектора
, а напрям вектора 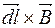 співнапрямлений з вектором
співнапрямлений з вектором 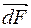 .
.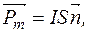
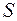 – площа обмежена струмом,
– площа обмежена струмом, 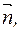 − одиничний вектор нормалі до
− одиничний вектор нормалі до 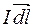 :
:
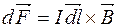 .
.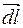 (мал. 93). Очевидно, що для того, щоб обчислити силу, з якою магнетне поле діє на весь провідник чи його частину скінченної довжини, слід додати всі елементарні сили
(мал. 93). Очевидно, що для того, щоб обчислити силу, з якою магнетне поле діє на весь провідник чи його частину скінченної довжини, слід додати всі елементарні сили  .
. На мал. 94 (а) показаний прямокутний чи круглий контур зі струмом (промінь зору паралельний до площини контура), який довільно зорієнтований щодо силових ліній магнетного поля. З цього малюнка видно, що згідно з законом Ампера, напрям сили, з якою поле діє на кожну сторону контура, різний, причому сили, які діють на сторону, яку ми бачимо і протилежну до неї, рівні за величиною і протилежні за напрямом – вони стискають контур.
На мал. 94 (а) показаний прямокутний чи круглий контур зі струмом (промінь зору паралельний до площини контура), який довільно зорієнтований щодо силових ліній магнетного поля. З цього малюнка видно, що згідно з законом Ампера, напрям сили, з якою поле діє на кожну сторону контура, різний, причому сили, які діють на сторону, яку ми бачимо і протилежну до неї, рівні за величиною і протилежні за напрямом – вони стискають контур.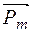 паралельним до них (мал. 94 (б)). У цьому стані на контур діятиме лише сила, яка його розтягає. Причому цей стан рівноваги є стійким, тобто за найменшого відхилення від нього виникають сили, які повертають контур у стан рівноваги.
паралельним до них (мал. 94 (б)). У цьому стані на контур діятиме лише сила, яка його розтягає. Причому цей стан рівноваги є стійким, тобто за найменшого відхилення від нього виникають сили, які повертають контур у стан рівноваги.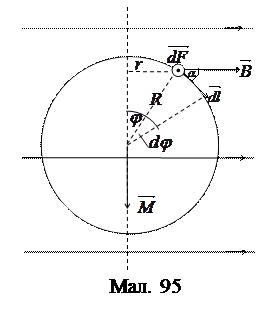 Виберемо на контурі довільний елемент струму
Виберемо на контурі довільний елемент струму 
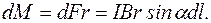

 − довжина контура.
− довжина контура. . З малюнка видно, що
. З малюнка видно, що 
 i
i  . Підставивши ці вирази в останній інтеграл, дістанемо
. Підставивши ці вирази в останній інтеграл, дістанемо

 спрямований вздовж осі обертання (за правилом правого гвинта), тобто туди ж, куди і векторний добуток
спрямований вздовж осі обертання (за правилом правого гвинта), тобто туди ж, куди і векторний добуток  то
то

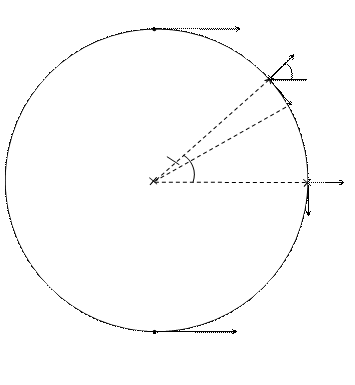 Ми вже з’ясували (задача 151), що вільний контур зі струмом в однорідному магнетному полі повертатиметься доти, доки його магнетний момент не буде паралельним до вектора магнетної індукції, після чого обертальний момент зникне і залишиться лише сила, яка розтягає контур.
Ми вже з’ясували (задача 151), що вільний контур зі струмом в однорідному магнетному полі повертатиметься доти, доки його магнетний момент не буде паралельним до вектора магнетної індукції, після чого обертальний момент зникне і залишиться лише сила, яка розтягає контур.

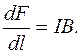


 мал. 97), то сила Ампера буде лише стискати контур і він буде нерухомим. Проте за найменшого відхилення контура від цього стану виникне момент сил Ампера, який буде лише збільшувати це відхилення, повертаючи контур, як вже нам відомо (задача 151), у стійкий стан з паралельним напрямом його магнетного моменту щодо зовнішнього магнетного
мал. 97), то сила Ампера буде лише стискати контур і він буде нерухомим. Проте за найменшого відхилення контура від цього стану виникне момент сил Ампера, який буде лише збільшувати це відхилення, повертаючи контур, як вже нам відомо (задача 151), у стійкий стан з паралельним напрямом його магнетного моменту щодо зовнішнього магнетного  поля.
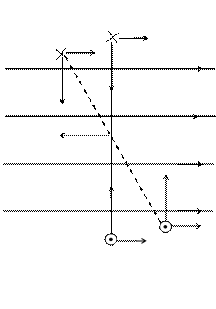
поля. Розглянемо випадок магнетного поля, для якого вектор індукції всюди однаковий за напрямом, але різний за величиною. Графічно таке поле зображується паралельними прямими, густота яких різна в різних областях простору (мал. 98 (а)). Бачимо, що контур, як і у випадку однорідного поля, повертатиметься, доки його вектор магнетного моменту не буде співнапрямлений з вектором індукції (мал. 98 (б)). Проте наступна його поведінка відрізнятиметься від поведінки в однорідному полі, а сам
Розглянемо випадок магнетного поля, для якого вектор індукції всюди однаковий за напрямом, але різний за величиною. Графічно таке поле зображується паралельними прямими, густота яких різна в різних областях простору (мал. 98 (а)). Бачимо, що контур, як і у випадку однорідного поля, повертатиметься, доки його вектор магнетного моменту не буде співнапрямлений з вектором індукції (мал. 98 (б)). Проте наступна його поведінка відрізнятиметься від поведінки в однорідному полі, а сам  е, внаслідок різної індукції поля у різних місцях контура сила Ампера буде різною (більшою в області сильнішого поля), їхня рівнодійна не дорівнюватиме нулеві і, як наслідок, контур буде переміщуватися в область сильнішого поля.
е, внаслідок різної індукції поля у різних місцях контура сила Ампера буде різною (більшою в області сильнішого поля), їхня рівнодійна не дорівнюватиме нулеві і, як наслідок, контур буде переміщуватися в область сильнішого поля.


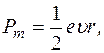
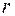 − радіус орбіти електрона.
− радіус орбіти електрона.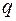 стержня довжиною
стержня довжиною 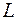 , який обертається з кутовою швидкістю
, який обертається з кутовою швидкістю  .
. створює магнетний момент (мал. 99)
створює магнетний момент (мал. 99)
 створюється обертальним рухом заряду
створюється обертальним рухом заряду 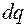 , який є на елементі радіуса стержня
, який є на елементі радіуса стержня  , то з означенням сили струму
, то з означенням сили струму

 − лінійна густина заряду стержня.
− лінійна густина заряду стержня.

 ми підставили
ми підставили  .
.