 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Розділ IV. Електричні коливання і електромагнетні хвилі
Тема 1. Змінний струм Фізичні явища · Синусоїдний змінний струм – змінний струм, сила якого змінюється з часом за синусоїдним законом. · Ефективне (діюче) значення змінного струму – це таке значення сили постійного струму, за якого його середня теплова потужність така ж, як і за цього змінного струму (інакше кажучи: це таке значення сили постійного струму, який дає такий самий тепловий ефект, як і цей змінний струм). · Квазістаціонарне коло змінного струму – це таке коло змінного струму, розміри якого значно менші за довжину електромагнетної хвилі, яка поширюється вздовж кола. · Активний опір– це векторна складова повного опору кола змінного струму, яка спричинена наявністю опору провідників. · Ємнісний опір – це векторна складова повного опору кола змінного струму, яка спричинена наявністю в цьому колі ємності (позначення
· Індуктивний опір – це векторна складова повного опору кола змінного струму, спричинена наявністю в цьому колі індуктивності (позначення
· Коефіцієнт трансформації – це відношення напруг у вторинній та первинній обмотках трансформатора (позначення k).
· Повний опір – це величина
· Резонанс напруг – це явище різкого зростання струму в нерозгалуженому колі змінного струму за умови рівності ємнісного та індуктивного опорів. · Резонанс струмів– це явище різкого зменшення сили струму в нерозгалуженій ділянці розгалуженого кола за умови рівності ємнісного та індуктивного опорів.
Фізичні поняття ·Фазна напруга – це напруга між нульовим і фазним проводом трифазного генератора. ·Лінійна напруга – це напруга між будь-якими двома фазними проводами трифазного генератора.
Фізичні системи й прилади ·Трансформатор– це прилад для підвищення чи зниження напруги змінного струму. ·Генератор змінного струму – прилад, який генерує змінну електрорушійну силу. ·Асинхронний двигун – це електричний двигун трифазного змінного струму, в якому обертове магнетне поле статора індукує в роторі струм, який, своєю чергою зазнаючи дії цього магнетного поля, спричиняє обертання ротора.
Задачі (229) На основі закону електромагнетної індукції встановимо часову залежність ЕРС індукції, яка виникає в контурі площею
Враховуючи, що
Величина
тобто рівномірне обертання контура в постійному магнетному полі спричиняє виникнення в ньому синусоїдної ЕРС. Це явище і закладено в основу роботи генераторів синусоїдної ЕРС. (230) Доведемо, що середнє значення синусоїдної змінної ЕРС за період дорівнює нулеві. За формулою середнього значення функції
Очевидно, що середнє значення змінної ЕРС і за будь-який проміжок часу, що дорівнює великій кількості періодів, дорівнює нулю. Проте це не означає, що змінний струм не здатний виконувати роботу.
(231) Покажемо, що середнє значення теплової потужності змінного струму за період не дорівнює нулеві. Середнє значення теплової потужності змінного струму за період (чи багато періодів)
де P – миттєве значення потужності, яке як і для постійного струму
звідки бачимо, що середнє значення теплової потужності змінного струму не дорівнює нулеві (на відміну від середнього значення змінного струму).
(232) Знайдено зв'язок між ефективним та максимальним значенням змінної ЕРС. Згідно з означенням ефективного значення змінного струму, нам слід прирівняти середнє значення теплової потужності змінного струму за період до теплової потужності постійного струму, величина якого дорівнює ефективному значенню цього змінного струму. У результаті розв’язання попередньої задачі ми знайшли, що середнє значення теплової потужності змінного струму
Потужність постійного струму з ефективним значенням цього змінного струму
Прирівнявши
тобто ефективне значення змінного струму є меншим за його максимальне (амплітудне значення) в
(233) Обґрунтуємо застосовність закону Ома та правил Кірхгофа до миттєвих, амплітудних та ефективних значень сили струму й напруги. Дійсно, оскільки миттєві значення сили струму та напруги можна вважати постійними, до них можна застосувати закон Ома та правила Кірхгофа. Амплітудне значення сили струму чи напруги – це одне з миттєвих значень, а ефективне значення – це зменшене в
(234) Доведемо, що в активному резисторі сила змінного струму збігається за фазою з напругою.
Величина
звідки бачимо, що під знаком синуса у виразі для струму як і у виразі для ЕРС одна і та ж величина
(235) Доведемо, що в індуктивному резисторі сила струму відстає від напруги за фазою на
Застосуємо до цього кола друге правило Кірхгофа. Оскільки в колі є дві електрорушійні сили – ЕРС джерела та ЕРС самоіндукції, яка виникає внаслідок протікання змінного струму через соленоїд (задача 194) і немає напруг (бо немає активного опору), то згідно з другим правилом Кірхгофа
звідки
Після інтегрування
Для того, щоб порівняти фази сили струму та ЕРС, слід останній вираз для сили струму представити через функцію sin, як і вираз для ЕРС.
де З отриманої рівності для сили струму Крім того, в ході цього виводу ми отримали, що максимальне значення сили струму
звідки бачимо, що величина
(236) Доведемо, що в ємнісному резисторіопорі сила струму випереджає напругу за фазою на
Розглянемо коло, у якому є, крім змінної ЕРС, тільки конденсатор з ємністю С (мал. 151). У цьому колі є одна ЕРС – це ЕРС джерела
Напругу
звідки
Для того, щоб отримати вираз для сили струму, продиференціюємо останню рівність за часом.
або
Представимо останню рівність через функцію sin
звідки, а також з закону зміни ЕРС Представимо закон зміни сили струму так (237) Розкриємо геометричний спосіб додавання гармонічних коливань (векторна модель додавання гармонічних коливань). Нехай нам слід додати декілька величин, які змінюються за гармонічним законом (наприклад, напруг, сил струмів чи величин будь-якої іншої природи). Для простоти візьмемо два гармонічні коливання
де Під кутом З малюнка бачимо, що проекція вектора
Отже, сумою двох чи більше гармонічних величин є гармонічна величина, амплітуду і фазу якої можна знайти геометрично. Додавання гармонічних коливань зводиться до додавання векторів, довжини яких дорівнюють амплітудам цих гармонічних коливань, а кут між цими векторами дорівнює різниці фаз між цими коливаннями. Слід зауважити, що згадані вектори не представляють відповідні фізичні величини, а представляють коливання фізичних величин, причому як векторних, так і скалярних.
(238) Користуючись векторною моделлю додавання гармонічних коливань виведемо закон Ома для ділянки кола змінного струму.
Силу струму, яка є однаковою всюди на цій ділянці кола, зобразимо вектором вздовж осі х (мал. 154). Оскільки напруга на активному опорі збігається за фазою з силою струму (задача 234), то вектор
Згідно з законом Ома, для ділянки кола
або підставивши
Ця рівність і є законом Ома для ділянки кола змінного струму. Якщо величину
Зауважимо, що при побудові векторної діаграми ми зображали не амплітудні значення відповідних величин, як це мало би бути згідно з векторною моделлю гармонічних коливань (задача 237), а ефективні їхні значення. Проте це нічого не змінює, бо ефективні значення відрізняються від амплітудних лише множником
(239) Установимо умову, за якої сила струму в нерозгалуженому колі змінного струму буде максимальною (умову резонансу напруг).
Із закону Ома для ділянки кола змінного струму маємо, що за умови
тобто за умови рівності ємнісного та індуктивного опорів, сила струму на цій ділянці кола буде максимальною
Крім того бачимо, що за умови резонансу напруг повний опір ділянки кола є мінімальним і дорівнює активному опору.
(240) Установимо умову, за якої сила струму в розгалуженому колі змінного струму буде максимальною (умову резонансу струмів).
Скористаємось векторною моделлю додавання гармонічних коливань. Оскільки напруга на всіх трьох опорах однакова, то вздовж осі х відкладаємо вектор напруги (мал. 156). Вектор, який представляє силу струму в активному опорі
звідки бачимо, що за умови
сила струму в нерозгалуженій ділянці кола буде мінімальною.
Якщо ж вилучити опір R (
(241) Установимо зв'язок середньої потужності змінного струму з ефективними значеннями сили струму та напруги. Згідно з виразом середнього значення функції, знайдемо середнє значення потужності змінного струму за період.
де P – миттєве значення потужності, яке, очевидно, пов’язане з миттєвими значеннями сили струму і напруги такою ж формулою, як і для постійного струму
Підставивши останній вираз замість підінтегральної функції та інтегруючи, дістанемо
і врахувавши формулу зв’язку між максимальними та ефективними значеннями як сили струму, так і напруги
Як бачимо, потужність змінного струму залежить не тільки від ефективних значень сили струму та напруги, а й від зсуву фаз між ними
(242) Покажемо, що коефіцієнт трансформації трансформатора дорівнює відношенню кількості витків вторинної та первинної обмотки. Якщо до однієї з обмоток трансформатора (первинної) принднати джерело змінного струму, то цей струм створить змінний магнетний потік через площу контурів як первинної, так і вторинної обмоток (мал. 157), що, своєю чергою, згідно з законом електромагнетної індукції, спричинить виникнення ЕРС в обидвох обмотках.
З цих двох формул
Покажемо, що для ненавантаженого трансформатора ЕРС За законом Ома для ділянки кола з ЕРС
звідки
Для ненавантаженого трансформатора
З цих рівностей та рівності (1)
Вважаючи потужності в обидвох обмотках однаковими, дістанемо з формули потужності для
(243) Покажемо, як принципово можна отримати трифазний стст.рум і напишемо закон його зміни з часом.
Згадаємо, що однофазну змінну ЕРС отримують обертанням дротяної рамки чи обмотки в магнетному полі (задача 228). Трифазну ЕРС можна отримати обертанням магнетного поля зі сталою кутовою швидкістю
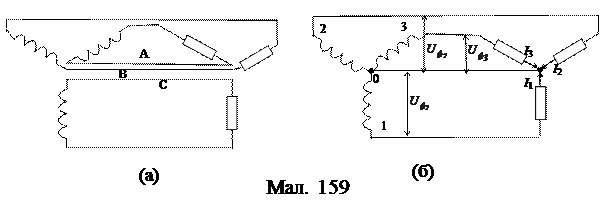
(244) За допомогою векторної діаграми для трифазних напруг встановимо співвідношення між лінійною та фазною напругами. З мал. 158 бачимо, що трифазний генератор забезпечує ЕРС для трьох кіл змінного струму, які схематично показані на мал. 159 (а). З’ясуємо, які напруги ми будемо мати, якщо з’єднати проводи А, В і С в один провід, який називають нульовим (мал. 159 (б)). Напруги між нульовим і кожним із фазних проводів 1, 2 і 3 називаються фазними, а напруги між самими проводами 1, 2 і 3 – лінійними. Установимо зв'язок між амплітудними значеннями лінійної та фазної напруг.
На мал. 160 показані нульовий та фазний проводи так, що вони спрямовані в площину малюнка. З цього малюнка бачимо, що
Згідно з векторною моделлю додавання гармонічних коливань, і враховуючи, що фази напруг З трикутника, складеного з двох фазних та однієї лінійної напруги, дістанемо зв'язок між їхніми амплітудними значеннями
Очевидно, що такий самий зв'язок буде і між ефективними значеннями цих напруг.
(245) Доведемо, що магнетне поле створене трифазним змінним струмом в трьох соленоїдах розміщених під кутом 1200 один до одного еквівалентне постійному полю з індукцією
Для цього знайдемо часову залежність результативного поля. На мал. 161 показані три соленоїди які розміщені один до одного під кутом 1200. Оскільки зсув фаз між струмами в кожному соленоїді становить 1200, то такий самий зсув фаз виникає і у відповідних магнетних полях тобто
де Виберемо систему координат як показано на мал. 162 і знайдемо відповідні проекції цих полів на вісь х.
а також х– проекцію результативного поля
Подібними діями отримаємо
і далі величину результативного поля
звідки бачимо, що величина поля стала, проте напрям вектора
звідки
що означає, що результативний вектор індукції магнетного поля рівномірно обертається з кутовою швидкістю Цю властивість трифазного струму створювати обертове магнетне поле використовують в трифазних двигунах, який вигідно вирізняється тим, що до рухомої його частини (якоря) не треба підводити струм (тому в ньому немає щіток), бо струм в ньому індукується цим обертовим полем. Далі цей індукований струм зазнає з боку обертового поля дії сили Ампера, яка і крутить якір. Саме через те, що в асинхронних двигунах немає щіток які іскрять їх потужність може бути будь-якою великою.
Поиск по сайту: |
 )
) .
. ).
). .
.

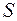 , що обертається з кутовою швидкістю
, що обертається з кутовою швидкістю  в однорідному магнетному полі з індукцією
в однорідному магнетному полі з індукцією 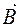 .
. Унаслідок обертання контура в магнетному полі в ньому виникає ЕРС індукції, спричинена зміною магнетного потоку крізь цей контур (мал. 148). Оскільки поле однорідне, а контур плоский, то магнетний потік
Унаслідок обертання контура в магнетному полі в ньому виникає ЕРС індукції, спричинена зміною магнетного потоку крізь цей контур (мал. 148). Оскільки поле однорідне, а контур плоский, то магнетний потік  і тоді, згідно з законом електромагнетної індукції
і тоді, згідно з законом електромагнетної індукції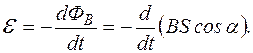
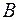 і
і 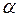 , будучи кутом між вектором
, будучи кутом між вектором  дістанемо
дістанемо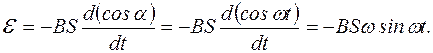
 має розмірність ЕРС і є її максимальним значенням, тому позначимо її
має розмірність ЕРС і є її максимальним значенням, тому позначимо її  . Дістанемо закон зміни ЕРС у контурі
. Дістанемо закон зміни ЕРС у контурі


 (очевидно, що миттєве значення змінного струму можна вважати постійним). Після підстановки цього виразу в останню рівність дістанемо
(очевидно, що миттєве значення змінного струму можна вважати постійним). Після підстановки цього виразу в останню рівність дістанемо



 до
до  дістанемо
дістанемо
 рази, що означає: для того, щоб від змінного струму отримати такий самий тепловий ефект, як і від заданого постійного струму, його амплітудне значення має бути в
рази, що означає: для того, щоб від змінного струму отримати такий самий тепловий ефект, як і від заданого постійного струму, його амплітудне значення має бути в  Розглянемо коло, у якому є синусоїдна ЕРС та активний опір R (мал. 149). Згідно з законом Ома, сила струму в колі
Розглянемо коло, у якому є синусоїдна ЕРС та активний опір R (мал. 149). Згідно з законом Ома, сила струму в колі
 має одиницю виміру сили струму і є її максимальним значенням, тому позначимо її
має одиницю виміру сили струму і є її максимальним значенням, тому позначимо її  . Дістанемо закон зміни сили струму
. Дістанемо закон зміни сили струму
 , тобто фази сили струму і напруги збігаються.
, тобто фази сили струму і напруги збігаються. .
. Розглянемо коло, у якому є лише синусоїдна ЕРС
Розглянемо коло, у якому є лише синусоїдна ЕРС 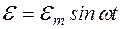 та соленоїд з індуктивністю L (мал. 150).
та соленоїд з індуктивністю L (мал. 150).





 та рівності для ЕРС
та рівності для ЕРС  ,
, має зміст опору. Цю величину називають індуктивним опором
має зміст опору. Цю величину називають індуктивним опором 
 та одна напруга – це напруга на конденсаторі
та одна напруга – це напруга на конденсаторі  , тому, згідно з другим правилом Кірхгофа
, тому, згідно з другим правилом Кірхгофа



 ,
, .
.
 , де
, де  звідки бачимо, що величина
звідки бачимо, що величина  має зміст опору, її називають ємнісним опором і позначають
має зміст опору, її називають ємнісним опором і позначають 

 – різниця фаз між цими коливаннями.
– різниця фаз між цими коливаннями. , а під кутом
, а під кутом  – вектор довжиною
– вектор довжиною  (мал. 152).
(мал. 152). на вісь у – це є величина
на вісь у – це є величина  , проекція вектора
, проекція вектора  – величина
– величина  , а проекція суми цих векторів – сума величин
, а проекція суми цих векторів – сума величин 
 Нехай на ділянці кола є послідовно з’єднані всі три типи опорів – активний, індуктивний та ємнісний (мал. 153).
Нехай на ділянці кола є послідовно з’єднані всі три типи опорів – активний, індуктивний та ємнісний (мал. 153). відкладаємо співнапрямленим з вектором
відкладаємо співнапрямленим з вектором  . Напруга на індуктивному опорі випереджає силу струму на
. Напруга на індуктивному опорі випереджає силу струму на  відкладаємо під кутом
відкладаємо під кутом  відкладаємо під кутом
відкладаємо під кутом 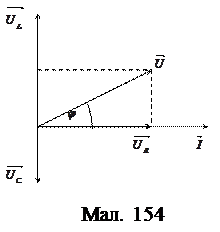 Напруга на ділянці кола U зобразиться вектором, який є сумою векторів
Напруга на ділянці кола U зобразиться вектором, який є сумою векторів  та
та 
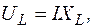

 , тому
, тому

 звідки
звідки

 позначити буквою
позначити буквою  і назвати повним опором, то закон Ома для ділянки кола змінного струму набуде вигляду
і назвати повним опором, то закон Ома для ділянки кола змінного струму набуде вигляду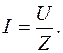
 .
.

 Розглянемо коло з паралельно з’єднаними R, L і C (мал. 155).
Розглянемо коло з паралельно з’єднаними R, L і C (мал. 155). , відкладаємо паралельно до вектора напруги внаслідок збігу їхніх фаз (задача 234). Оскільки сила струму в ємнісному опорі випереджає напругу на
, відкладаємо паралельно до вектора напруги внаслідок збігу їхніх фаз (задача 234). Оскільки сила струму в ємнісному опорі випереджає напругу на  відкладаємо під прямим кутом до вектора U в бік випередження (задача 236). Вектор
відкладаємо під прямим кутом до вектора U в бік випередження (задача 236). Вектор  та
та 


 ), то ця сила струму дорівнюватиме нулеві.
), то ця сила струму дорівнюватиме нулеві.
 де
де  – зсув фаз між струмом і напругою, який в колі з різними типами опорів не дорівнює ні нулеві, ні
– зсув фаз між струмом і напругою, який в колі з різними типами опорів не дорівнює ні нулеві, ні  (дивись мал. 154 та 156).
(дивись мал. 154 та 156).

 ще називають коефіцієнтом потужності, який намагаються зробити якомога більшим, тобто кут
ще називають коефіцієнтом потужності, який намагаються зробити якомога більшим, тобто кут  .
.

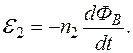
 (1)
(1)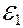 та
та  практично дорівнюють напругам.
практично дорівнюють напругам.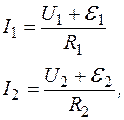

 , а
, а 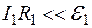 через мале значення сили струму
через мале значення сили струму  , що спричинене великим індуктивним опором первинної обмотки, тому
, що спричинене великим індуктивним опором первинної обмотки, тому




 . Очевидно, що в кожній з обмоток внаслідок явища електромагнетної індукції виникне ЕРС, яка зміщена відносно іншої за фазою на
. Очевидно, що в кожній з обмоток внаслідок явища електромагнетної індукції виникне ЕРС, яка зміщена відносно іншої за фазою на 
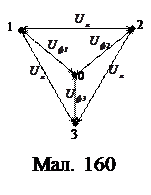
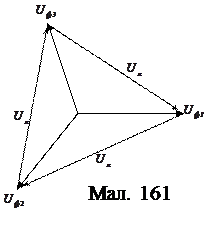
 та
та  зміщені одна відносно одної на
зміщені одна відносно одної на 
 , яке обертається з кутовою швидкістю, що дорівнює циклічній частоті змінного струму.
, яке обертається з кутовою швидкістю, що дорівнює циклічній частоті змінного струму.

 – магнетні поля створені відповідними соленоїдами.
– магнетні поля створені відповідними соленоїдами.



 безперервно змінюється, причому так, що
безперервно змінюється, причому так, що
