 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 3. Циркуляція і потік вектора індукції магнетного поля
Фізичні поняття ·Циркуляція вектора магнетної індукції вздовж замкненого контура довжиною L –це вираз
де · Потік вектора магнетної індукції через поверхню площею S −це величина
(мал. 108).
Постулати Ø Теорема про циркуляцію вектора магнетної індукції: циркуляція вектора магнетної індукції вздовж будь-якого замкненого контура пропорційна до потоку вектора густини струму через поверхню, обмежену цим контуром
де Ø Теорема Остроградського-Гауса для магнетного поля: потік вектора індукції магнетного поля через будь-яку замкнену поверхню дорівнює нулеві, тобто
Основні одиниці фізичних величин ·Один ампер – це сила такого постійного струму, який, протікаючи у двох паралельних нескінченно довгих та нескінченно тонких прямих проводах, що є у вакуумі на відстані 1 метр один від одного, спричиняє силу їхньої взаємодії на одиницю довжини
Задачі (166) На основі означення одиниці фізичної величини ампера визначимо числове значення магнетної сталої. Ми вже показали (задача 165), що два паралельні нескінченно довгі провідники з струмами притягуються або відштовхуються. Для того, щоб знайти величину цієї сили, розраховану на одиницю довжини провідників, напишемо вираз індукції поля прямого нескінченно довгого струму
Тоді сила Ампера, яка діє з боку цього поля на другий провід
звідки
З означення одного ампера випливає, що за умови
Як бачимо, числове значення магнетної сталої буде різним у різних системах одиниць, бо вона залежить від основних одиниць: одиниці сили струму, довжини, маси та часу.
Раніше ми з’ясували (задача 158), що будь-яка силова лінія прямого струму – це коло з центром на прямій, вздовж якої тече струм і, відповідно, вектор
Тепер розглянемо більш загальний випадок, тобто коли прямий струм охоплено будь-яким проте плоским контуром (мал. 110). Представимо цей контур як послідовність нескінченної кількості колових дуг та радіальних відрізків. Очевидно, що циркуляція вектора
Якщо контур не плоский, то результат буде такий самий – усі відрізки, паралельні до струму, будуть нормальними до вектора індукції і не вноситимуть вкладу в інтеграл, тобто циркуляція вектора Отже, ми довели, що для прямого струму теорема про магнетну циркуляцію дійсно має місце. Зауважимо, що ця теорема насправді є постулатом, вона ще має назву: закон Ампера.
(168) На основі теореми про магнетну циркуляцію покажемо, що для випадку струмів будь-якої форми, які течуть у проводах
де Дійсно, для скінченної кількості струмів (мал. 111) інтеграл переходить в алгебраїчну суму, тобт
і теорема про магнетну циркуляцію набуває вигляду
(169) Представимо теорему про магнетну циркуляцію у диференціяльній формі. Для цього застосуємо теорему Стокса, яка стверджує, що циркуляція будь-якого вектора вздовж замкненого контура дорівнює потоку ротора цього вектора через поверхню, обмежену цим контуром. Дістанемо
Звідси та згідно з теоремою про магнетну циркуляцію
Оскільки в обидвох частинах рівності є поверхневі інтеграли по одній і тій же поверхні, то мають бути рівними й підінтегральні вирази, тобто
Це рівняння є диференціяльною формою теореми про магнетну циркуляцію.
(170) За допомогою теореми про магнетну циркуляцію знайдемо вираз для індукції магнетного поля тороїда.
Цей контур охоплює N струмів однакового напряму і величини І, тому, згідно з теоремою про магнетну циркуляцію,
звідки
або враховуючи, що
Бачимо, що магнетне поле всередині тороїда таке ж за величиною, як і всередині нормального соленоїда з такою ж густотою витків (задача 162). Це і не дивно, бо тороїд можна сконструювати згинанням нормального соленоїда так, щоб його вісь набула форми кола. Щодо напряму вектора індукції, то всередині соленоїда воно практично однорідне (однакове як за величиною так і за напрямом) а в тороїді однакове лише за величиною.
(171) На основі теореми про магнетну циркуляцію знайдемо вираз для індукції магнетного поля всередині нормального соленоїда. Ми вже отримали формулу для індукції поля на осі нормального соленоїда на основі закону Біо-Савара-Лапласа (воно практично однакове всюди всередині соленоїда). Покажемо, що це можна зробити за допомогою теореми про магнетну циркуляцію, причому простіше. Щоб застосувати згадану теорему, нам слід вибрати замкнений контур, який охоплює всі струми величиною І. У ролі цього контура візьмемо контур ABCD (мал. 113) і обчислимо циркуляцію вектора
Позаяк на відрізку AB вектори
або
де L − довжина соленоїда, N − кількість його витків. З останньої рівності
або
де n − густота витків соленоїда.
(172) Представимо теорему Остроградського-Гауса для магнетного поля в диференціяльній формі. Для цього застосуємо математичну теорему, яка також називається теоремою Остроградського-Гауса і яка, по суті, переводить поверхневий інтеграл в об’ємний.
тобто потік будь-якого вектора Згідно з цією теоремою, теорема Остроградського-Гауса для магнетного поля набуває вигляду
звідки, оскільки
Остання рівність представляє ту ж саму теорему Остроградського-Гауса для магнетного поля, проте в диференціяльній формі.
(173) Покажемо, що теорема Остроградського-Гауса для магнетного поля свідчить про замкненість силових ліній магнетного поля, що, своєю чергою, може трактуватися як відсутність у природі магнетних зарядів. Дійсно, рівність нулеві потоку вектора магнетної індукції через будь-яку замкнену поверхню говорить про те, що кожна силова лінія, яка входить в область, обмежену цією поверхнею, мусить вийти з цієї області, тому ця силова лінія має бути замкненою, що, зі свого боку означає, що ніде немає її джерела, тобто немає магнетного заряду.
Тема 4. Сила Лоренца Фізичні явища · · Магнетоопір (магнеторезистивний ефект) − це явище зміни опору провідника чи напівпровідника в магнетному полі. · Циклотронний резонанс − це раптове зростання магнетоопору провідника чи напівпровідника за умови збігу циклотронної частоти носіїв струму з частотою фотона. Фізичні поняття · Сила Лоренца − це сила, яка діє на точковий заряд з боку електричного та магнетного полів (позначення · Питомий заряд частинки − це відношення заряду частинки до її маси. · Циклотронна частота − це частота обертання зарядженої частинки навколо вектора індукції магнетного поля. Фізичні системи й прилади · Сенсор Голла – прилад, який працює за принципом ефекту Голла й призначений для вимірювання індукції магнетного поля. · Мас-спектрометр – прилад, який працює на основі закономірностей руху заряджених частинок в електричному й магнетному полях і призначений для вимірювання мас йонів з метою установлення хемічного складу певного зразка. · Прискорювачі заряджених частинок – прилади, за допомогою яких заряджені частинки прискорюються в електричному та магнетному полях до великих швидкостей. · Магнетогідродинамічний (МГД) генератор – генератор постійної ЕРС, дія якого базується на розділені електричних зарядів магнетним полем.
Задачі
(174) Установимо вираз для сили Лоренца. З означення сили Лоренца та принципу суперпозиції сил вип.ливає, що вона дорівнює сумі сил, які діють на точковий заряд з боку електричного
Вираз для сили з боку електричного поля нам відомий: Розглянемо конкретний точковий заряд – електрон. Силу, яка діє з боку магнетного поля на цей електрон, знайдемо як силу, яка діє з боку цього поля на всі рухомі електрони, які є в заданому відрізку провідника, поділену на їхню кількість. Сила, яка діє з боку магнетного поля на всі електрони відрізка провідника зі струмом dl, – це сила Ампера, вираз якої, як нам відомо, має вигляд
Представивши силу струму згідно з її означенням як
Враховуючи, що
Поділивши ліву й праву частину цієї формули на dN, дістанемо силу, яка діє на один електрон
або
Оскільки вектор дрейфової швидкості електрона
Для будь-якого точкового позитивного заряду q
і вираз для сили Лоренца
(175) Вкажемо на відносність магнетного поля.
Нехай позитивний точковий заряд рухається зі швидкістю
Спостерігач, який рухається із зарядом, зафіксує ту ж саму силу, проте заряд відносно нього буде нерухомим, тому, з погляду цього спостерігача, це сила електричного поля, напруженість якого
і силові лінії якого є нормальними до силових ліній магнетного поля, яке бачить спостерігач у лабораторній системі. Отже, спостерігач у лабораторній системі сприймає поле як магнетне, тоді як спостерігач у системі, зв’язаній з зарядом, як електричне.
(176) Порівняємо силу електричної та магнетної взаємодії між двома точковими зарядами. Розглянемо два точкові позитивні заряди, які рухаються зі швидкістю
де
де Отже, сила магнетної взаємодії цих двох зарядів
а її модуль
Водночас сила електричної взаємодії
і її модуль
Порівнюючи ці дві сили, маємо
що означає, що за малих порівняно зі швидкістю світла швидкостей сила електричної взаємодії набагато більша за силу магнетної взаємодії, і для того, щоб ці дві сили зрівнялися, заряди мали би рухатися зі швидкістю світла. Крім того, бачимо, що спостерігач у системі відліку, зв’язаній з зарядами, фіксує тільки електричне поле і, відповідно, електричне відштовхування між зарядами, тоді як спостерігач у лабораторній системі − як електричне, так і магнетне поле і, відповідно, силу електричного відштовхування та силу магнетного притягання, тобто рівнодійну цих сил, модуль якої з двох останніх рівнянь
(177) Знайдемо циклотронну частоту точкового заряду, який потрапив у магнетне поле нормально до його силових ліній.
Так частинка буде рухатися дугою кола, радіус якого знайдемо з умови рівності відцентрової сили інерції, яка при цьому виникла, силі магнетного поля.
звідки, враховуючи що
і на основі формули зв’язку лінійної і кутової швидкостей
Як бачимо, циклотронна частота не залежить від швидкості, з якою частинка влетіла в магнетне поле, а лише від її маси та індукції магнетного поля.
(178) Знайдемо радіус і крок гвинтової лінії, вздовж якої буде рухатися заряджена частинка, яка потрапила в магнетне поле під довільним кутом Спочатку покажемо, що сила магнетного поля визначається лише нормальною до магнетного поля складовою вектора швидкості заряду. Для цього розкладемо вектор швидкості на дві складові (мал. 118): нормальну й паралельну до поля та напишемо вираз для сили магнетного поля
Радіус гвинтової лінії знайдемо з умови рівності сили магнетного поля відцентровій силі інерції
звідки
або, підставивши
Крок h гвинтової лінії знайдемо з умови, що за один період заряд, рухаючись вздовж поля зі швидкістю
(179) Визначимо питомий заряд електрона, якщо він, будучи прискореним різницею потенціялів Потрапивши в магнетне поле, електрон рухатиметься дугою кола так, що відцентрова сила інерції дорівнюватиме силі магнетного поля.
звідки питомий заряд електрона
Швидкість електрона
звідки
а радіус кола R з рівності
звідки
Підставивши знайдені вирази для
(180) Визначимо питомий заряд електрона методом Томсона, а саме: якщо він, рухаючись нормально до силових ліній взаємно-нормальних та однорідних електричних та магнетних полів, не зазнав відхилення. Той факт, що електрон, незважаючи на присутність електричного та магнетного полів, не зазнав їхньої дії, означає, що сили, які на нього діють з боку цих полів, однакові за величиною та протилежні за напрямом, тобто
або, враховуючи вирази цих сил
звідки швидкість, з якою електрон має прийти в область дії цих двох полів
Ця швидкість задається прискорювальною напругою
З двох останніх рівностей
Якщо електричне поле створюється конденсатором, відстань між пластинами якого d і напруга на них U, а магнетне поле – соленоїдом з густотою витків n і силою струму I, то підставивши в останню формулу
дістанемо
Практично це робиться так: в електронно-променевій трубці (мал. 120) за відсутності електричного та магнетного полів пучок електронів прискорений напругою
(181) Знайдемо масу однозарядного йона, який потрапив на фотопластинку у масс-спектрографі Бейнбріджа на відстані L від щілини.
або
Усі інші йони будуть відхилені цими полями. Отже, йони зі швидкістю
потрапляють в магнетне поле
звідки, а також з формули для
За напрямом дуги (вліво чи вправо), згідно з правилом правого гвинта для векторного добутку векторів, визначаємо також знак йона.
(182) Пояснимо механізм виникнення ефекту Голла і виразимо напругу Голла через індукцію магнетного поля і силу струму. Помістимо метал чи напівпровідник зі струмом у магнетне поле, лінії індукції якого нормальні до струму (мал. 122).
або, представивши E через напругу Голла
звідки
Представивши дрейфову швидкість електронів через густину струму й концентрацію, а густину струму через силу струму та розміри зразка, дістанемо
(183) Покажемо, що вимірявши експериментально напругу Голла можна визначити концентрацію та рухливість носіїв струму в металі чи напівпровіднику. З формули для напруги Голла
бачимо, що вимірявши силу струму I, індукцію поля B, розмір зразка
а також їхню рухливість
де U − напруга на його кінцях.
(184) Пояснимо роботу прискорювача заряджених частинок − циклотрона.
Циклотрон (мал. 123) складається з двох металевих півколових посудин з вакуумом, які називають дуантами. Однорідне магнетне поле нормальне до площини дуантів. Джерело заряджених частинок розміщене в центрі циклотрона. Якщо до дуантів приєднати джерело змінної ЕРС з частотою, яка збігається з циклотронною частотою, то частинка почне свій рух в електричному полі, яке буде її прискорювати незалежно від того, де вона є. З кожним обертом частота залишається сталою, а швидкість та радіус орбіти зростають (задача 177). У результаті частинка з великою швидкістю вилітає з циклотрона.
(185) Пояснимо роботу магнетогідродинамічного генератора (МГД-генератора).
Явище розділення зарядів у МГД- генераторі подібне до ефекту Голла з тією різницею, що в МГД- генераторі як позитивний, так і негативний заряди рухаються в одному напрямі, а в провіднику зі струмом – в протилежних. Це приводить до того, що різнойменні заряди в МГД- генераторі відхиляються до протилежних електродів, тоді як у провіднику зі струмом в магнетному полі – до одного і того ж електрода.
(186) Пояснимо, як виникає явище “північне сяйво”.
Поиск по сайту: |


 − елемент довжини контура.
− елемент довжини контура.

 – магнетна стала.
– магнетна стала.

 в точці, що розміщена на відстані
в точці, що розміщена на відстані  від нього (задача 159)
від нього (задача 159)

 .
.
 м, – сила взаємодії, що припадає на одиницю довжини має бути
м, – сила взаємодії, що припадає на одиницю довжини має бути  Н/м, тому
Н/м, тому
 (167) Перевіримо теорему про циркуляцію вектора магнетної індукції для прямого струму.
(167) Перевіримо теорему про циркуляцію вектора магнетної індукції для прямого струму. Спочатку розглянемо частковий випадок замкненого контура, який збігається з однією з силових ліній магнетного поля цього струму (мал. 109). Обчислимо циркуляцію магнетної індукції вздовж цього контура.
Спочатку розглянемо частковий випадок замкненого контура, який збігається з однією з силових ліній магнетного поля цього струму (мал. 109). Обчислимо циркуляцію магнетної індукції вздовж цього контура. є дотичним до нього. Оскільки вектор елемента довжини кола
є дотичним до нього. Оскільки вектор елемента довжини кола  і застосувавши формулу індукції поля прямого струму (задача 159), дістанемо
і застосувавши формулу індукції поля прямого струму (задача 159), дістанемо .
. Ми отримали, що циркуляція вектора магнетної індукції прямого струму вздовж замкненого контура, який збігається з будь-якою із силових ліній, пропорційна до сили струму, а оскільки сила струму – це потік вектора густини струму (задача 72 з розділу 2), то ця циркуляція пропорційна до потоку густини струму, причому з коефіцієнтом пропорційності
Ми отримали, що циркуляція вектора магнетної індукції прямого струму вздовж замкненого контура, який збігається з будь-якою із силових ліній, пропорційна до сили струму, а оскільки сила струму – це потік вектора густини струму (задача 72 з розділу 2), то ця циркуляція пропорційна до потоку густини струму, причому з коефіцієнтом пропорційності  в повній відповідності до постулату про циркуляцію вектора магнетної індукції.
в повній відповідності до постулату про циркуляцію вектора магнетної індукції.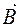 вздовж радіальних відрізків дорівнює нулеві, бо скалярний добуток
вздовж радіальних відрізків дорівнює нулеві, бо скалярний добуток  там дорівнює нулеві як скалярний добуток взаємно-нормальних векторів. Для колових дуг
там дорівнює нулеві як скалярний добуток взаємно-нормальних векторів. Для колових дуг  тому
тому

 − алгебраїчна сума струмів, яка охоплена будь-яким контуром довжиною L.
− алгебраїчна сума струмів, яка охоплена будь-яким контуром довжиною L. о
о
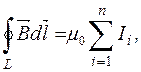




 Нехай тороїд має радіус R і кількість витків N (мал. 112). Виберемо замкнений контур так, щоб він збігся з осьовою лінією тороїда. Оскільки вектор
Нехай тороїд має радіус R і кількість витків N (мал. 112). Виберемо замкнений контур так, щоб він збігся з осьовою лінією тороїда. Оскільки вектор 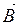 в усіх точках вибраного нами контура однаковий і спрямований вздовж дотичної до нього, то
в усіх точках вибраного нами контура однаковий і спрямований вздовж дотичної до нього, то  і
і
 ,
,
 – це густота витків n
– це густота витків n
 , то відповідні скалярні добутки
, то відповідні скалярні добутки  дорівнюють нулеві і тому циркуляція вектора
дорівнюють нулеві і тому циркуляція вектора 

 і враховуючи однорідність поля всередині соленоїда маємо
і враховуючи однорідність поля всередині соленоїда маємо




 через замкнену поверхню дорівнює інтегралу від дивергенції цього вектора за об’ємом, обмеженим цією поверхнею.
через замкнену поверхню дорівнює інтегралу від дивергенції цього вектора за об’ємом, обмеженим цією поверхнею.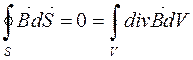 ,
, ,
,
 Ефект Голла − це явище виникнення різниці потенціялів між двома протилежними поверхнями провідника чи напівпровідника зі струмом паралельним до цих поверхонь у магнетному полі яке нормальне до струму і паралельне до цих поверхонь (мал. 114).
Ефект Голла − це явище виникнення різниці потенціялів між двома протилежними поверхнями провідника чи напівпровідника зі струмом паралельним до цих поверхонь у магнетному полі яке нормальне до струму і паралельне до цих поверхонь (мал. 114). ).
). та магнетного
та магнетного  полів.
полів.
 , тому нам залишилось віднайти вираз для сили з боку магнетного поля.
, тому нам залишилось віднайти вираз для сили з боку магнетного поля.
 , а заряд
, а заряд 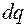 як
як  , де
, де  – кількість електронів в елементі довжини провідника dl, дістанемо
– кількість електронів в елементі довжини провідника dl, дістанемо
 – це дрейфова швидкість електрона, маємо
– це дрейфова швидкість електрона, маємо


 є протилежним до елемента струму
є протилежним до елемента струму  , то
, то


 відносно спостерігача в лабораторній системі відліку в магнетному полі (для простоти нормально до силових ліній (мал. 115)). Очевидно, що на нього діятиме сила цього поля B
відносно спостерігача в лабораторній системі відліку в магнетному полі (для простоти нормально до силових ліній (мал. 115)). Очевидно, що на нього діятиме сила цього поля B


 в лабораторній системі відліку (мал. 116). На другий заряд, з боку магнетного поля, створеного першим зарядом, діє сила
в лабораторній системі відліку (мал. 116). На другий заряд, з боку магнетного поля, створеного першим зарядом, діє сила


 − напруженість електричного поля цього заряду.
− напруженість електричного поля цього заряду.
 .
.

 ,
,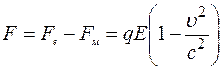 .
. Як тільки заряджена частинка потрапить у магнетне поле, на неї почне діяти сила з боку цього поля яка, згідно з правилом правого гвинта для векторного добутку, буде спрямована нормально як до вектора індукції, так і до вектора швидкості (мал. 117). Це спричинить зміну траєкторії частинки, що, своєю чергою, спричинить зміну напряму швидкості і, відповідно, напряму сили.
Як тільки заряджена частинка потрапить у магнетне поле, на неї почне діяти сила з боку цього поля яка, згідно з правилом правого гвинта для векторного добутку, буде спрямована нормально як до вектора індукції, так і до вектора швидкості (мал. 117). Це спричинить зміну траєкторії частинки, що, своєю чергою, спричинить зміну напряму швидкості і, відповідно, напряму сили.

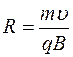
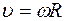

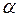 до його силових ліній.
до його силових ліній.
 Аналогічно можемо показати, що сила магнетного поля визначається нормальною до вектора швидкості складовою вектора
Аналогічно можемо показати, що сила магнетного поля визначається нормальною до вектора швидкості складовою вектора  .
.


 ,
,
 , проходить вздовж поля саме цю відстань, тобто
, проходить вздовж поля саме цю відстань, тобто
 потрапивши в нормальне до його швидкості магнетне поле з індукцією
потрапивши в нормальне до його швидкості магнетне поле з індукцією 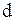 , пройшовши відстань
, пройшовши відстань  (мал. 119).
(мал. 119).


 визначається прискорювальною напругою
визначається прискорювальною напругою 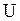 з рівності
з рівності





 ,
,


 .
.



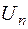 потрапляє, очевидно, в центр екрана (точка О). Далі включають магнетне поле і пучок електронів відхиляється у точку А. Після того включають електричне поле такої напруженості, щоб пучок електронів знову повернувся у центр екрана. Це буде означати, що сили, які діють на електрони з боку обидвох полів, компенсують одна одну. Вимірявши прискорювальну напругу
потрапляє, очевидно, в центр екрана (точка О). Далі включають магнетне поле і пучок електронів відхиляється у точку А. Після того включають електричне поле такої напруженості, щоб пучок електронів знову повернувся у центр екрана. Це буде означати, що сили, які діють на електрони з боку обидвох полів, компенсують одна одну. Вимірявши прискорювальну напругу  відстань між пластинами конденсатора d та напругу на них U, силу струму в соленоїді I та густоту його витків n за останньою формулою, можемо обчислити питомий заряд електрона.
відстань між пластинами конденсатора d та напругу на них U, силу струму в соленоїді I та густоту його витків n за останньою формулою, можемо обчислити питомий заряд електрона.
 На мал. 121 схематично показано масс-спектрометр Бейнбріджа. Електричне поле
На мал. 121 схематично показано масс-спектрометр Бейнбріджа. Електричне поле 

 ,
,

 де на них діє сила цього магнетного поля, і під дією якої вони описують дугу кола, радіус якого знаходимо з умови рівності цієї сили відцентровій силі інерції
де на них діє сила цього магнетного поля, і під дією якої вони описують дугу кола, радіус якого знаходимо з умови рівності цієї сили відцентровій силі інерції

 Нехай основні носії заряду в цьому матеріялі − електрони. На них почне діяти сила магнетного поля яка відхилятиме їх до верхньої грані що порушить електронейтральність в усьому об’ємі зразка і спричинить виникнення електричного поля, спрямованого від нижньої до верхньої грані. Це поле діятиме на електрони з силою протилежною за напрямом до сили магнетного поля, причому воно зростатиме в міру нагромадження електронів на верхній грані. За умови рівності цих сил процес розділення зарядів припиниться. Напишемо цю умову
Нехай основні носії заряду в цьому матеріялі − електрони. На них почне діяти сила магнетного поля яка відхилятиме їх до верхньої грані що порушить електронейтральність в усьому об’ємі зразка і спричинить виникнення електричного поля, спрямованого від нижньої до верхньої грані. Це поле діятиме на електрони з силою протилежною за напрямом до сили магнетного поля, причому воно зростатиме в міру нагромадження електронів на верхній грані. За умови рівності цих сил процес розділення зарядів припиниться. Напишемо цю умову , дістанемо
, дістанемо
 .
.

 в напрямі магнетного поля та напругу Голла
в напрямі магнетного поля та напругу Голла 

 В основі принципу роботи циклотрона лежить той факт, що частота обертання зарядженої частинки навколо вектора індукції магнетного поля, а це, як відомо, циклотронна частота, не залежить від її швидкості (задача 177).
В основі принципу роботи циклотрона лежить той факт, що частота обертання зарядженої частинки навколо вектора індукції магнетного поля, а це, як відомо, циклотронна частота, не залежить від її швидкості (задача 177). У камері (мал. 124) робоче тіло нагрівається до температури приблизно 3000 К, тобто до стану плазми, і через сопло виривається у канал, у якому є магнетне поле, нормальне до напряму руху плазми. Під дією сили магнетного поля позитивно заряджені частинки відхилятимуться до верхнього електрода, а негативно заряджені – до нижнього. Якщо до електродів приєднати споживача, то в колі потече струм, причому, оскільки процес розділення зарядів безперервний, то на місце носіїв струму, які втратили на споживачі свою енергію дрейфового руху, приходять нові, тобто ми маємо джерело ЕРС.
У камері (мал. 124) робоче тіло нагрівається до температури приблизно 3000 К, тобто до стану плазми, і через сопло виривається у канал, у якому є магнетне поле, нормальне до напряму руху плазми. Під дією сили магнетного поля позитивно заряджені частинки відхилятимуться до верхнього електрода, а негативно заряджені – до нижнього. Якщо до електродів приєднати споживача, то в колі потече струм, причому, оскільки процес розділення зарядів безперервний, то на місце носіїв струму, які втратили на споживачі свою енергію дрейфового руху, приходять нові, тобто ми маємо джерело ЕРС. Відомо, що Сонце, крім світла та іншого електромагнетного випромінювання, випромінює потік частинок − електронів, протонів та йонів, – який дістав назву “сонячний вітер”. Відбувається це внаслідок високої температури Сонця – кінетична енергія частинок настільки велика, що вона перевищує роботу виходу за межі тяжіння Сонця (це та сама термоемісія з тією різницею, що частинка мусить долати не тільки силу затримуючого електричного поля, а й силу тяжіння).
Відомо, що Сонце, крім світла та іншого електромагнетного випромінювання, випромінює потік частинок − електронів, протонів та йонів, – який дістав назву “сонячний вітер”. Відбувається це внаслідок високої температури Сонця – кінетична енергія частинок настільки велика, що вона перевищує роботу виходу за межі тяжіння Сонця (це та сама термоемісія з тією різницею, що частинка мусить долати не тільки силу затримуючого електричного поля, а й силу тяжіння). Якщо б цей “сонячний вітер” проник до нас, то життя на Землі було б неможливим, а захищає нас від цього убивчого потоку кор.пускул магнетне поле Землі. Дійсно, заряджена частинка, наприклад, електрон потрапивши в магнетне поле Землі (мал. 125) під кутом до силової лінії, почне рухатися гвинтовою лінією навколо цієї силової лінії (задача 178). Коли вона досягає атмосфери Землі, а це, як видно з малюнка, відбувається біля магнетних полюсів, то, бомбардуючи атоми, спричиняє їх світіння.
Якщо б цей “сонячний вітер” проник до нас, то життя на Землі було б неможливим, а захищає нас від цього убивчого потоку кор.пускул магнетне поле Землі. Дійсно, заряджена частинка, наприклад, електрон потрапивши в магнетне поле Землі (мал. 125) під кутом до силової лінії, почне рухатися гвинтовою лінією навколо цієї силової лінії (задача 178). Коли вона досягає атмосфери Землі, а це, як видно з малюнка, відбувається біля магнетних полюсів, то, бомбардуючи атоми, спричиняє їх світіння.