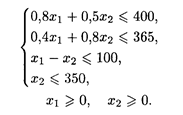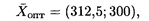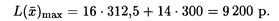Алгоритм решения задач

1. Находим область допустимых решений системы ограни­чений задачи.

2. Строим вектор .

3. Проводим линию уровня L₀, которая перпендикулярна .

4. Линию уровня перемещаем по направлению вектора для задач на максимум и в направлении, противоположном , для задач на минимум.

Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допусти­мых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум, и ее решение находится по формуле

где 0 ≤ t ≤ 1, ₁ и ₂ — оптимальные решения в угловых точках ОДР.

Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение це­левой функции в ней.

20.3. Выбор оптимального варианта выпуска изделий

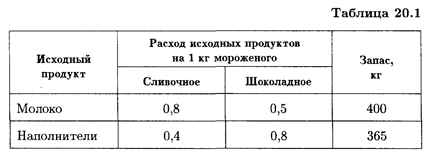
Фирма выпускает 2 вида мороженого: сливочное и шоко­ладное. Для изготовления мороженого используются два ис­ходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в табл. 20.1.

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не бо­лее чем на 100 кг. Кроме того, установлено, что спрос на шо­коладное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного — 14 р.

Какое количество мороженого каждого вида должна про­изводить фирма, чтобы доход от реализации продукции был максимальным?

Решение. Обозначим: x₁ — суточный объем выпуска сли­вочного мороженого, кг; x₂ — суточный объем выпуска шоко­ладного мороженого, кг.

Составим математическую модель задачи.

Целевая функция будет иметь вид

при ограничениях:

OABDEF — область допустимых решений (рис. 20.1). Строим вектор (1, 1). Линия уровня L₀ задается уравнением

Перемещаем линию уровня по направлению вектора . Точ­кой выхода L₀ из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, за­данных уравнениями:

Решая систему, получим координаты точки D (312,5; 300), в которой и будет оптимальное решение, т.е.

при этом

Таким образом, фирма должна выпускать в сутки 312,5 кг сли­вочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9 200 р.

Поиск по сайту: