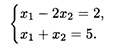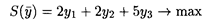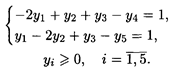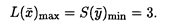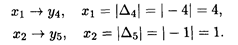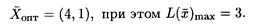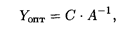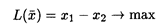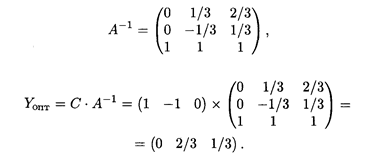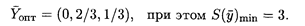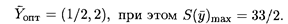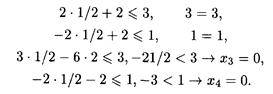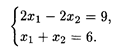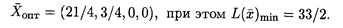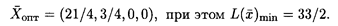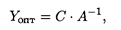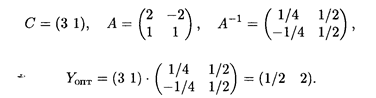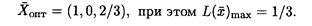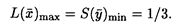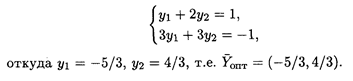|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение двойственных задач
Решение симметричных задач
Рассмотрим решение задач с использованием теорем двойственности.
Решим исходную задачу графическим методом, получим На основании 1-й теоремы двойственности
Так как x1, х2 > 0, то по 2-й теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств:
Подставим
Тогда система ограничений двойственной задачи примет вид
Откуда Пусть дано решение двойственной задачи По 1-й теореме двойственности L(
Откуда Рассмотрим решение задач методом, основанным на взаимно однозначном соответствии между переменными: основным переменным исходной задачи соответствуют балансовые переменные двойственной, и наоборот. Для этого решим двойственную задачу симплексным методом:
при ограничениях:
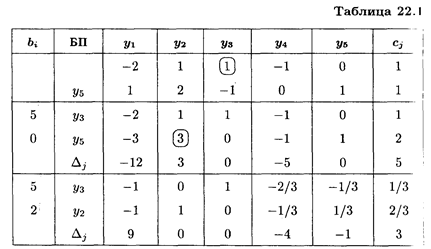
Из табл. 22.1 следует, что
На основании 1-й теоремы двойственности получаем
Решение другой задачи найдем по соответствию между переменными:
Значение xj определяем по последней симплексной таблице в строке Δi в соответствующем столбце, причем значения xj берем по модулю:
Таким образом, решение исходной задачи:
Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле
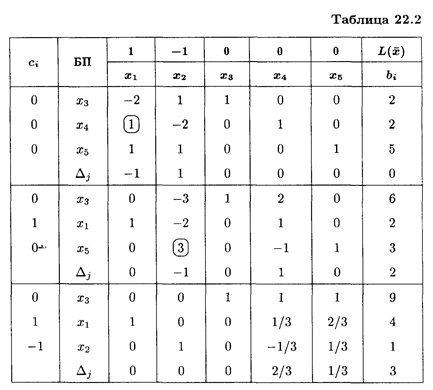
где С — матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи; А-1 — обратная матрица для матрицы А, являющейся матрицей коэффициентов базисных переменных системы ограничений исходной задачи в оптимальном решении. Решим симплексным методом исходную задачу вида
при ограничениях:
Из табл. 22.2 следует, что
тогда
Таким образом, решение двойственной задачи следующее:
Решение несимметричных задач
Рассмотрим решение задач с использованием теорем двойственности.
Решив двойственную задачу графическим методом, получим
По 1-й теореме двойственности L( Подставим
Так как х3 = х4 = 0, то система ограничений исходной задачи примет вид
Решая данную систему, получим
Рассмотрим решение задач с использованием обратной матрицы. Пусть решение исходной задачи
Решение двойственной задачи найдем по формуле
где
Таким образом,
Решение смешанных двойственных задач
Смешанные двойственные задачи можно решать с использованием теорем двойственности.
Найдем оптимальное решение двойственной задачи:
По 1-й теореме двойственности
Так как х1 > 0, x3 > 0, то по 2-й теореме двойственности первое и третье ограничения двойственной задачи выполняются в виде равенств:
Поиск по сайту: |

 опт = (4, 1), при этом L(
опт = (4, 1), при этом L( 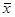 )mах = 3.
)mах = 3.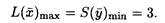
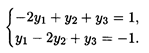
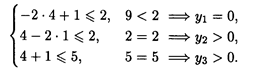
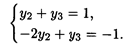
 опт = (0, 2/3, 1/3), при этом S(
опт = (0, 2/3, 1/3), при этом S(  )min = 3.
)min = 3.