 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Термодинамика негіздері⇐ ПредыдущаяСтр 14 из 14
Термодинамиканың бірінші бастамасы. Изопроцестер. Қайтымды және қайтымсыз процесстер. Карно циклі, оның п.ә.к.-і. Карно теоремасы. Термодинамиканың екінші бастамасы және оның физикалық мағынасы. Темодинамиканың екінші бастамасының статистикалық сипаттамасы . Энтропия. Термодинамиканың бірінші бастамасы (заңы). Механикалық энергиясы өзгермей ішкі энергиясы ғана өзгеретін термодинамикалық жүйені қарастырайық. Жүйенің ішкі энергиясы түрлі процестер нәтижесінде өзгеруі мүмкін: 1) жұмыс жасау арқылы; 2) жылу беру (қыздыру) арқылы. Демек, жылу мөлшері дегеніміз жүйенің сыртқы денелер арқылы жылу алмасу процесі кезінде энергиясының артуы (түрлі температурадағы денелердің жылу алмасуы немесе ішкі энергияларымен алмасуы). Механикалық қозғалыс энергиясы жылулық қозғалыстың энергиясына және керісінше ішкі энергия механикалық қозғалыс энергиясына айнала алады. Бұл айналуларда энергияның бір түрден екінші түрге айналу және сақталу заңы орындалады. Термодинамиканың 1 заңы термодинамикалық процестерге қатысты энергияның сақталу заңы болып табылады. Термодинамиканың 1 заңы көптеген тәжірибелердің нәтижесі. Ішкі энергиясы
Егер жүйе процесс аяғында өзінің бастапқы күйіне қайта оралатын болса, онда ішкі энергияның өзгерісі нольге тең болады:
Демек, термодинамиканың бірінші заңы бойынша сырттан берілетін энергиядан артық жұмыс жасайтын машина жасау мүмкін емес, яғни мәңгі двигательдің 1-ші түрін жасау мүмкін емес (термодинамиканың 1 заңының тағы бір тұжырымдамасы). Газдың көлемі өзгергендегі жұмысы. Көлемі өзгергендегі газдың сыртқы күштерге қарсы жұмысын табу үшін нақты процесті қарастырайық. Мысалы, газ толтырылған поршені бар цилиндрді алайық. Цилиндр мен поршень арасындағы газ көлемі ұлғайғанда поршеньді Мұндағы
10.1 сурет Термодинамиканың I заңын изопроцестерге қолдану. Изопроцестер - бір негізгі параметрі тұрақты болатын процестер, тепе-теңдік процестерге жатады. Осы процестерге термодинамиканың I заңының қолданылуын қарастырайық. 1. Изохоралық процесс
Изохоралық процесте газ жұмыс жасамайды, яғни Термодинамиканың I заңынан демек, изохоралық процесс үшін газға берілетін жылу оның ішкі энергиясының ұлғаюына жұмсалады: 10.2 сурет
2. Изобаралық процесс (p = const). Изобаралық процестің диаграммасы р, V координаталарында абсцисса осіне параллель болады . Изобаралық процесте газ көлемі
және диаграммада тік бұрыштың ауданымен анықталады.
Сонда изобаралық ұлғаю кезіндегі жұмыс:
10.3сурет
Бұл теңдеуден универсал газ тұрақтысының R физикалық мағынасы көрінеді. Егер температураның айырымы
газдың ішкі энергиясы dU – ға өзгереді: 3. Изотермиялық процесс (T= const). Изотермиялық процесс Бойль-Мариотт заңымен анықталады: pV=const. Изотермиялық процестің диаграммасы р, V координаталарында гипербола болады. Газ изотермиялық жолмен ұлғайғанда жасалатын жұмыс
Ішкі энергиясы өзгермейді: Изотермиялық процесс үшін: демек газға берілетін жылу мөлшері сыртқы күштерге қарсы жұмыс жасауға жұмсалады:
Термодинамиканың І заңы бойынша температура тұрақты болуы үшін газға изотермиялық процесс кезінде сыртқы жұмысқа тең жылу мөлшерін беру керек. Адиабаттық процесс. Адиабаттық процесс деп жүйелер арасында және қоршаған ортамен жылу алмасу болмайтын δQ = 0 процесті айтады. Адиабаттық процеске тез өтетін процестер жатады. Мысалы, дыбыстың ортада таралуы. Дыбыс толқынының таралу жылдамдығы өте үлкен, сондықтан толқын мен орта арасында энергия алмасуға үлгермейді. Адиабаттық процестер двигательдердің ішкі жануында (цилиндрдегі жанғыш қоспалардың ұлғаюы және сығылуы), салқындатқыштарда және т.б. қолданылады. Термодинамиканың 1 заңын пайдаланып адиабаттық процестің теңдеуінің қорытып шығарылуын қарастыралық. Термодинамиканың 1 заңынан δQ = dU + δА адиабаталық процесс үшін δА = - dU (10.9) яғни сыртқы жұмыс ішкі энергияның өзгеруі арқылы жасалады. δА= рdV және CV = Идеал газ теңдеуін дифференциалдап, мынаны аламыз: рdV + Vdр = - теңдеулерден Т-ны алып тастаймыз, ол үшін екі теңдеудің қатынасын қарастырамыз: 1 +
адиабата процесінің теңдеулеріндегі
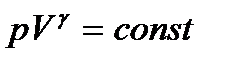 изотермаға қарағанда өзгеше, тік изотермаға қарағанда өзгеше, тік  болады. Адиабаталық сығылу кезіндегі (1-3 бөлігі) газ қысымының көбеюін изотермиялық сығылу кезіндегідей оның көлемінің азаюымен ғана емес, температураның көбеюімен де түсіндіруге болады. болады. Адиабаталық сығылу кезіндегі (1-3 бөлігі) газ қысымының көбеюін изотермиялық сығылу кезіндегідей оның көлемінің азаюымен ғана емес, температураның көбеюімен де түсіндіруге болады.
10.4 сурет
Адиабаталық процесс кезіндегі жұмысты есептеп шығарайық, формуласын рdV = - Егер газ V1 көлемнен V2 көлемге дейін адиабаталық ұлғайса, онда оның температурасы T1 - ден Т2–ге дейін азаяды және идеал газ ұлғайған кезде жасалатын жұмыс А = - Менделеев- Клапейрон теңдеуін пайдаланып, T, V немесе p, T айнымалы- ларына көшу формуласын түрлендіріп, адиабаталық ұлғаю жұмысын жазуға болады: А = Адиабаталық ұлғаю кезіндегі жасалатын жұмыс суреттің 1-2 бөлігі. 1,2,V2,V1, 1 - штрихталған ауданмен анықталады, изотермиялық ұлғаю кезінде жасалатын жұмыстан кіші болады. Себебі адиабалық процесс кезінде газ суиды, ал изотермиялық процесс кезінде сырттан эквивалент жылу мөлшерін алу есебінен температура тұрақты болады. Политропты процесс.Қарастырылған изохоралық, изобаралық, изотермиялық, адиабаталық процестердің барлығына ортақ бір ерекшелік – аталған процестерде жылусыйымдылықтың тұрақты болуы. Изохоралық (V=const) және изобаралық (р=const) процестерде жылусыйымдылық
мұндағы n – политроп көрсеткіші, оның мәні мына өрнекпен анықталады:
1) С = 0 болғанда n = γ теңдеуінен адиабатаның теңдеуі шығады. 2) С = 3) С =Сз , n = 0 – изобаралық процестің теңдеуі. 4) С =Сv , n = Қайтымды және қайтымсыз процестер.Дөңгелек процесс немесе цикл деп жүйе бірнеше күйден өтіп барып бастапқы күйге қайта оралу процесін айтады. Циклдің диаграммасы тұйық қисық. Идеал газдың циклін 2 процеске бөлуге болады. 1. Газдың ұлғаюы (1-2); 2. Газдың сығылуы (2-1). Газ ұлғайған кезде жасалған жұмыс оң dV >0, яғни жұмыс 1а2V2 V11 фигураның ауданына тең болады, ал сығылу жұмысы теріс dV<0 болады да, 2в1V1V22 фигураның ауданымен анықталады. Демек, цикл ішінде газдың жасаған жұмысы тұйық қисықтың ауданымен анықталады. Егер цикл ішінде оң жұмыс жасалса A = Тура цикл жылу двигательдерінде қолданылады. Жылу двигательдері деп жұмысты сырттан алынған жылу арқылы периодты түрде жасайтын двигательдерді айтады. Кері цикл салқындатқыш машиналарда қолданылады. Салқындатқыш машиналар деп сыртқы күштердің жұмысы арқылы жылу температурасы төмен денеден жоғары денеге берілетін машиналарды айтады. Дөңгелектік процесс нәтижесінде жүйе бастапқы күйіне қайта оралады, яғни ішкі энергияның толық өзгерісі нульге тең. Дөңгелек процесс үшін термодинамиканың 1 заңын жазайық: Q = ΔU + А, ΔU = 0, бұдан Q = А, Демек цикл ішінде жасалған жұмыс сырттан берілген жылуға тең. Бірақ цикл нәтижесінде жүйе жылуды алуы да, беруі де мүмкін, сондықтан Q = Q1 - Q2, Q1 - жүйенің алған жылу мөлшері, Q2 - жүйенің берген жылу мөлшері. Дөңгелек процесс үшін термиялық пайдалы әсер коэффициенті
Термодинамикалық жүйе 1 күйден 2 күйге өткен кезде бір параметрдің мәні өзгеретін процесті термодинамикалық процесс деп атайды. Егер термодинамикалық процесс кезінде жүйе 1 күйден 2 күйге, яғни i – күйлерден өтсін делік, жүйе i – күйлерден және 2 күйден өтіп, 1 күйге қайта айналып келсе, жүйеде және оны қоршаған ортада ешқандай өзгеріс байқалмаса, ондай процесті қайтымды процесс деп атайды.Үйкеліс болмаса, маятниктің қозғалысы қайтымды процесс болар еді. Алайда үйкелісті жою мүмкін емес, сондықтан маятниктің қозғалысы қайтымды қайтымды процеске жатпайды. Табиғатта қайтымды процесті байқау мүмкін емес. Бірақ тепе-теңдік процестерді қайтымды процесс ретінде қарастыруға болады. Себебі, кез-келген процесс ішінде аралық күй бар, ол күй термодинамикалық тепе-теңдікке сәйкес келеді, тепе-теңдік күй процесстің тура, немесе кері өтуіне тәуелді емес. Нақты процестерде энергия жоғалады, мысалы үйкеліс, жылу өткізгіштік нәтижесінде. Қайтымды процесс дегеніміз нақты процестерді идеалдау болып табылады. Табиғаттағы кейбір процестерді қайтымды деуге болады, егер олар экономика тұрғысынан тиімді болса немесе нақты жылу двигательдерінің п.ә.к. көтеруге мүмкіндік берсе. Егер жүйе бір күйден екінші күйге өткенде жүйенің өзінде, не болмаса қоршаған ортада өзгеріс болса, ондай процесті қайтымсыз процесс деп атайды. Өмірдегі процестердің бәрі қайтымсыз процесс болып саналады. Энтропия. Энтропия түсінігін алғаш енгізген Клаузиус. Оның физикалық мәнін қарастыру үшін изотермиялық процесс кезіндегі жылу мөлшерінің Q жылу беруші дененің температурасына Т қатынасын қарастырады.
Тұйық интегралдың нольге тең болуы интегралданып тұрған
Бұл функция жүйенің күйіне байланысты, ал жүйе сол күйге қандай жолмен келгеніне байланысты емес. Термодинамикада қайтымды процесс үшін энтропияның өзгерісі нольге тең болады: ΔS = 0, ал қайтымсыз процесс үшін өседі: ΔS > 0. Бұл өрнектерді біріктіріп, Клаузиус теңсіздігін алуға болады: ΔS ≥ 0. (10.16) Жазылған өрнектер тұйық жүйелер үшін де орындалады. Тұйық жүйенің энтропиясы өседі (қайтымсыз процесс) немесе тұрақты болады (қайтымды процесс). Егер жүйе тепе-теңдік жағдайда бір күйден екінші күйге өтсе, онда энтропияның өзгерісін төмендегідей анықтауға болады:
Энтропияның өзінің емес, энтропия өзгерісінің физикалық мағынасы бар. Идеал газ процесіндегі энтропияның өзгерісін қарастырайық. dU = δА = рdV =
Демек идеал газдың энтропиясының өзгерісі Адиабаталық процесс үшін δQ = 0, Изотермиялық процесс кезінде
Изохоралық процесс кезінде Энтропия - аддитивті шама. Жүйенің энтропиясы сол жүйеге кіретін барлық денелердің энтропиясының қосындысына тең. Демек, энтропияның масса, ішкі энергия, көлем сияқты аддитивті қасиеті бар. Термодинамиканың екінші заңы. Термодинамиканың 1 заңы энергияның сақталу және айналу заңы болып табылғанымен термодинамикалық процестің бағытын анықтай алмайды. Термодинамиканың 2 заңы табиғаттағы процестердің даму бағытын анықтайды. Энтропия түсінігін және Клаузиустың теңсіздігін қолдана отырып, термодинамиканың 2 заңын тұйық жүйедегі қайтымсыз процестер үшін энтропияның өсу заңы деуге болады: кез-келген тұйық жүйедегі қайтымсыз процесс сол жүйенің энтропиясы өсетіндей болып жүреді немесе қысқаша былай айтуға болады: тұйық жүйеде жүретін процестерде энтропия азаймайды. Тұйық емес (ашық) жүйелерде энтропия өсуі де, азаюы да, тұрақты болуы да мүмкін. Энтропия тұйық жүйедегі тек қана қайтымды процестер үшін тұрақты, ал тұйық жүйедегі қайтымсыз процестер үшін әрқашанда өседі. Тұйық жүйедегі қайтымсыз процестер үшін энтропияның өсу заңын Больцман формуласы былай түсіндіреді: энтропияның өсуі дегеніміз жүйенің ықтималдылығы аз күйден келесі ықтималдылығы көп күйге өтуі. Сонымен қатар Больцман формуласы статистикалық заңдылық тұрғысынан термодинамиканың 2 заңының тұжырымын береді. Термодинамиканың 2 заңы статистикалық заң болып табылады, тұйық жүйені құрайтын орасан көп бөлшектердің хаосты тәртіпсіз қозғалысының заңдылықтарын сипаттайды. Термодинамиканың 2 заңының Кельвин және Клаузиус бойынша тұжырымдамаларына тоқталайық. Кельвин бойынша тұжырымдамасы: сырттан энергия алмай жұмыс атқаратын машина жасау мүмкін емес, яғни мәңгі двигательдің 1 түрін жасау мүмкін емес. Клаузиус бойынша тұжырымдамасы: тек бір дененің сууы нәтижесінде жұмыс жасайтын машина жасау мүмкін емес. Кельвин және Клаузиус тұжырымдамалары бір-біріне эквивалентті. Егер тұйық жүйеде термодинамиканың 2 заңына қайшы келетін қиялдағы процесті жүргізсек, онда энтропия азаяды. Бұл Кельвин және Клаузиус тұжырымдамаларының эквивалентті екендігін көрсетеді. Термодинамиканың 1 және 2 заңдары термодинамикалық температура T= 0 К болғанда термодинамикалық жүйелерде энтропияның мәні қандай болатынын көрсетпейді. Сондықтан термодинамиканың 1 және 2 заңдары термодинамиканың 3 заңымен немесе Нернст- Планк теоремасымен толықтырылады: тепе-теңдік күйде термодинамикалық температура нольдік бөлікке жақындаған сайын барлық денелердің энтропиясы нольге ұмтылады
Энтропия аддитивті тұрақтыға дейін анықталатындықтан тұрақтыны нольге тең деп алуға болмайды. Нернст- Планк теоремасынан T= 0К болғанда Жылу двигательдері және салқындатқыш машиналар. Карно циклі және оның идеал газ үшін пайдалы әсер коэффициенті. Кельвин бойынша термодинамиканың екінші заңынан бір жылу көзін суыту арқылы жұмыс жасайтын двигательді - мәңгі двигательді жасау мүмкін емес. Жылу двигателінің жұмысын қарастырайық. Жылу двигателінің жұмыс істеу принципі 4.3-суретте көрсетілген. Температурасы жоғары Француз физигі Саади Карно жылу двигателі жұмыс істеу үшін оған кем дегенде екі жылу көзі керек екендігін, олардың температуралары әртүрлі болуы керектігін көрсетті, олай болмаса термодинамиканың екінші заңына қайшы келер еді. Жылу двигательдерінде қолданатын процеске қарсы процесс салқындатқыш машиналарда қолданылады. Салқындатқыш машинаның жұмыс істеу принципі 10.5-суретте көрсетілген. Цикл ішінде жүйедегі температурасы төмен
10.5 сурет Демек, жұмыс жасамай салқын денеден жылу алуға және оны жылы денеге беруге болмайды екен. Бұл термодинамиканың екінші заңының Клаузиус бойынша анықтамасы. Термодинамиканың екінші заңы бойынша температурасы төмен денеден температурасы жоғары денеге жылу мүлдем берілмейді деуге болмайды, себебі салқындатқыш машиналарда осы тәсіл қолданылады, бірақ бұл сыртқы күштердің жұмысы екендігін естен шығармау керек. Термодинамиканың екінші заңына сүйене отырып Карно мынадай теорема қорытып шығарды: периодты түрде жұмыс істейтін жылу машиналарының ішінен жылытқыштарының және салқындатқыштарының температуралары Карно ең тиімді қайтымды циклге анализ жасады. Ол цикл 2 изотермадан және 2 адиабатадан тұрады, Карно циклі деп аталады. Жұмысшы дене орнына идеал газ қолданылатын Карноның тура циклін қарастырайық. Изотермиялық ұлғаю және сығылу 1-2 және 3-4 қисықтарымен берілген, ал адиабаталық ұлғаю мен сығылу 2-3 және 4-1 қисықтарымен берілген (10.6-сурет).
10.6 сурет Изотермиялық процесс кезінде U = const, сондықтан жылытқыштан алынған Q жылу мөлшері газдың ұлғаю кезіндегі жасаған
Адиабаталық ұлғаю кезінде 2-3 бөлігі сыртқы ортамен жылу алмаспайды, демек ұлғаю жұмысы
Газдың салқындатқышқа изотермиялық сығылу кезінде берген Q2 жылу мөлшері сығылу жұмысына
Адиабаталық сығылу кезіндегі жұмыс
Дөңгелек процесс кезінде жасалатын жұмыс барлық жұмыстардың қосындысына тең және суреттегі боялған ауданмен анықталады (сурет 4.4):
Карно циклінің жылулық пайдалы әсер коэффициенті (4.1) өрнегіне сәйкес
2 - 3 және 4 - 1 адиабаттарына (3.18) формуласын қолдана отырып, төмендегі өрнектерді аламыз:
бұдан
(4.3), (4.4) өрнектерін (4.1) формуласына қойып және (4.5) өрнегін ескере отырып, Карно циклі үшін пайдалы әсер коэффициентін табамыз:
(4.6) формуласынан Карно циклінің пайдалы әсер коэффициенті қыздырғыш пен суытқыштың температуралары арқылы анықталатынын көреміз. П.ә.к. шамасын арттыру үшін қыздырғыш пен суытқыштың температураларының айырымын арттыру қажет. Мысалы, Бақылау сұрақтары: 1. Термодинамиканың бірінші бастамасын жазыңдар. 2. Газ көлемі ұлғайғандағы жұмыс. 3. Егер идеал газ тұрақты қысымда ұлғайса, ол қыза ма немесе салқындай ма? 4. Адиабат изотермаға қарағанда неге тіктеу? Адиабаттық сығылуда газдың температурасы қалай өзгереді 5. Қайтымды және қайтымсыз процесстердің өзгешелігі неде? Барлық нақты процесстер неге қайтымсыз? 6. Қыздырғыштан алынған жылу мөлшері түгелімен жұмысқа айналуы мүмкін бе? 7.Тұйық және тұйық емес жүйелерде энтропия қай бағытта өзгеруі мүмкін? 8.Энтропияға түсінік беріңдер (анықтамасы, әртүрлі процесстер үшін математикалық өрнегін және өлшемдерін). Әдебиеттер: НӘ3,6
№11 дәріс Нақты газдар Молекула аралық өзара әсер күштері. Молекулалардың әсерлік диаметрі. Ван-дер-Ваальс теңдеуі. Ван-дер-Ваальс изотермалары. Бірінші және екінші текті фазалық ауысулар. Клапейрон-Клаузиус теңдеуі. Молекула аралық өзара әсер күштері. Молекулалардың әсерлік диаметрі. Молекулалық-кинетикалық теорияда қолданылатын идеал газ моделін сиретілген нақты газдарды кейбір жағдайда жоғары температурада және төмен қысымда сипаттау үшін қолдануға болады. Бірақ, идеал газдың күй теңдеуін қорытып шығарған кезде, газ молекулалары арасындағы өзара әсерлесу және молекулалардың өлшемдері ескерілмегені естеріңізде болар. Қысым көбейгенде молекулалар арасындағы орташа арақашықтық азаяды, сондықтан молекулалардың көлемі мен олардың өзара әсерін ескеру маңызды. Мысалы, 1 м Нақты газдарды қарастырғанда олардың молекула аралық өзара әсер күштері ескеріледі, себебі нақты газдардың қасиеті молекулалардың өзара әсеріне тәуелді.Бұл күштер Табиғаттағы заттардың газ, сұйық, қатты күйлерде болуы, сол заттарды құрастырушы молекулалардың өзара әсерлесу сипатына байланысты болады. Сұйықтың өзі құйылған ыдыстың формасын сақтауы, оның молекулаларының арасында бірін-бірі тарту күші бар екенін, ал қатты денелердің өзінің формасын сақтауы, олардың молекулаларының арасында, тартылыс күшімен қатар, тербеліс күштері бар екенін көрсетеді. Молекулалардың арасындағы тартылыс, тебіліс күштері тең болған жағдайда ғана қатты денелер өзінің формасын сақтап тұра алады. Молекулалардың арасындағы әсерлесу - әсерлесудің электромагниттік түріне жатады. Заттың түрлі агрегаттық күйінің критериі ретінде ең кіші потенциялық энергия Егер Демек, кез-келген зат температураға байланысты газ, сұйық, қатты агрегат күйлерде бола алады екен. Бір агрегат күйден екінші агрегат күйге өту температурасы сол зат үшін Ван-дер-Ваальс теңдеуі. Ван-дер-Ваальс изотермалары. Нақты газдар үшін молекулалардың өлшемдерін және олардың бір-бірімен өзара әсерлесуін ескеру керек. Сондықтан идеал газ моделі мен оның күйін өрнектейтін Клапейрон-Менделеев теңдеуі нақты газдар үшін қолданылмайды. Молекуланың меншікті көлемін және молекула аралық күштерді ескере отырып, голланд физигі Ван-дер-Ваальс нақты газдардың күй теңдеуін Менделеев-Клапейрон теңдеуіне екі түзету енгізу арқылы қорытып шығарды. 1. Молекулалардың меншікті көлемін ескеру. Молекула алып тұрған көлемге тебу күшінің әсерінен басқа молекулалар кіре алмайды, сондықтан нақты газ молекуласы қозғала алатын көлем V емес, V- b тең, мұндағы b- молекуланың өзінің алатын көлемі, ол молекуланың төрт еселенген меншікті көлеміне тең болады. Мысалы, ыдыста екі молекула бар делік. Екі молекуланың кез-келгенінің центрі келесі молекуланың центріне d диаметрінен кіші қашықтыққа жақын келе алмайды. Демек, екі молекуланың центрі радиусы d-ға тең сфераның көлеміне енбейді, ол көлем сегіз молекуланың көлеміне немесе бір молекула үшін есептегенде төрт еселенген меншікті көлемге тең. 2. Молекулалардың өзара тартылуын ескеру. Молекула аралық тартылыс күші газдың ішінде қосымша қысымның пайда болуына алып келеді, ол қысым ішкі қысым деп аталады. Ван-дер-Ваальстің есептеуі бойынша ішкі қысым молярлық көлемнің квадратына кері пропорционал, яғни
мұндағы а – молекула аралық тартылыс күшін сипаттайтын Ван-дер-Ваальс тұрақтысы, ал Осы түзетулерді енгізе отырып, бір моль газ үшін Ван-дер-Ваальс теңдеуін – нақты газдың күй теңдеуін аламыз:
Газдың кез-келген зат мөлшері үшін
немесе
мұндағы а және b түзетулері әр газ үшін тәжірибе жүзінде анықталатын тұрақты шамалар, Ван-дер-Ваальс тұрақтылары деп аталады. Ван-дер-Ваальс изотермасы және оны эксперименталдық Эндрюс изотермасымен салыстыру.Нақты газды зерттеу үшін алдымен Ван- дер - Ваальс изотермаларын қарастырайық. Ол бір моль газ үшін берілген температурада Ван-дер-Ваальс теңдеуімен (11.2) анықталатын қысым мен көлемнің тәуелділік қисығы. Бұл қисықтар түрлі төрт температура ларға сәйкес келеді (11.1 сурет). 11.1 сурет Жоғары температурада
Бұл теңдеу берілген қысым мен температура үшін Кризистік температурадан төмен температурада газ тәріздес күйдегі затты бу деп атайды, ал сұйық күйімен тепе-теңдіктегі буды қаныққан бу деп атайды. Бұл қорытындылар ирланд ғалымы Эндрюстің тәжірибелерімен дәлелденді, ол көмірқышқыл газының көлемін изотермиялық жағдайда кішірейту арқылы осы қорытындыға келді. Тәжірибе жүзіндегі (Эндрюс) және теория жүзіндегі (Ван-дер Ваальс) изотермалардың бірінің бірінен айырмашылығы - бірінші жағдайда газдың сұйыққа айналуы горизонталь түзумен, екінші жағдайда толқынмен берілгені.
Егер изотермалардың горизонталь бөлігінің шеткі нүктелері арқылы сызық жүргізсек, онда заттың екі фазалық күйінің аймағын шектейтін қоңырау тәрізді қисық аламыз (11.3 сурет). Бұл қисық және кризистік изотерма p,
11.2 сурет 11.3 сурет 11.4 сурет Будың басқа газ тәріздес күйден айырмашылығы оның изотермиялық сығылу кезінде сұйыққа айналуы. Ал газ кризистік температурадан жоғары температурада қысымның ешбір мәнінде сұйыққа айналмайды. Газдарды сұйыққа айналдыру үшін алдымен оларды кризистік температурадан төмен температураға дейін суыту керек. Температурасы кризистік температурадан жоғары газды ешбір әдіспен сұйылтуға болмайды. Ван – дер - Ваальс изотермасын Эндрюстікімен салыстыра келіп (11.4 сурет, жоғарғы қисық), Эндрюс изотермасында заттың екі фазалы күйіне сәйкес келетін 2-6 түзу сызықты бөлігі бар екенін көреміз. Шындығында, кейбір жағдайда Ван-дер- Ваальс изотермасындағы 5 – 6 және 2 – 3 бөліктеріне сәйкес келетін күйлер болады. Бұл тұрақсыз күйлер метастабильді күйлер деп аталады. 2 – 3 бөлігі аса қызған сұйыққа, 5 – 6 бөлігі аса қаныққан буға сәйкес келеді. Төмен температураларда изотерма Нақты газдың ішкі энергиясы. Нақты газдың ішкі энергиясы оның молекулаларының жылулық қозғалысының кинетикалық энергиясынан және молекулааралық әсерлесудің потенциялық энергиясынан тұрады. Нақты газдардың потенциялық энергиясы молекула аралық тарту күштерімен анықталады, тарту күшінің болуы газда ішкі қысымның пайда болуына әкеледі (11.1):
Газ молекулаларының арасындағы тарту күшін жеңу үшін жасалатын жұмыс, механикадан білетініміздей, жүйенің потенциялық энергиясының артуына кетеді, сонда
Поиск по сайту: |
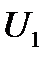 -ге тең жүйе (поршені бар цилиндрдің ішіндегі газ) Q жылу мөлшерін алды да ішкі энергиясы
-ге тең жүйе (поршені бар цилиндрдің ішіндегі газ) Q жылу мөлшерін алды да ішкі энергиясы 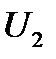 -ге тең жаңа күйге көшті делік, сонда жүйе сыртқы күштерге қарсы жұмыс жасады. Жүйеге берілетін жылу мөлшері және жүйе сыртқы күштерге қарсы жасайтын жұмыс оң шама болып есептелінеді. Тәжірибе көрсеткендей, энергияның сақталу заңы бойынша жүйе бір күйден екінші күйге қандай жолмен көшкеніне тәуелсіз ішкі энергияның өзгерісі
-ге тең жаңа күйге көшті делік, сонда жүйе сыртқы күштерге қарсы жұмыс жасады. Жүйеге берілетін жылу мөлшері және жүйе сыртқы күштерге қарсы жасайтын жұмыс оң шама болып есептелінеді. Тәжірибе көрсеткендей, энергияның сақталу заңы бойынша жүйе бір күйден екінші күйге қандай жолмен көшкеніне тәуелсіз ішкі энергияның өзгерісі 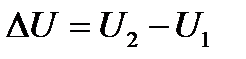 тең, демек жүйенің алатын жылу мөлшері Q мен сыртқы күштерге қарсы жасалатын жұмыстың А айырымына тең болады:
тең, демек жүйенің алатын жылу мөлшері Q мен сыртқы күштерге қарсы жасалатын жұмыстың А айырымына тең болады: немесе
немесе  теңдеуі термодинамиканың 1 заңының өрнегі болып табылады: жүйеге берілетін жылу мөлшері оның ішкі энергиясын өзгертуге және сыртқы күштерге қарсы жұмыс жасауға жұмсалады. Бұл теңдеуін дифференциалдап келесі өрнекті аламыз:
теңдеуі термодинамиканың 1 заңының өрнегі болып табылады: жүйеге берілетін жылу мөлшері оның ішкі энергиясын өзгертуге және сыртқы күштерге қарсы жұмыс жасауға жұмсалады. Бұл теңдеуін дифференциалдап келесі өрнекті аламыз:  немесе
немесе  .
.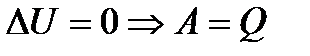 .
. - шексіз кіші арақашықтыққа жылжытады,сонда газдың сыртқы күштерге қарсы жасайтын жұмысы мынаған тең:
- шексіз кіші арақашықтыққа жылжытады,сонда газдың сыртқы күштерге қарсы жасайтын жұмысы мынаған тең:  .
. - поршеньнің ауданы,
- поршеньнің ауданы,  - жүйенің көлемінің өзгерісі. Демек,
- жүйенің көлемінің өзгерісі. Демек, 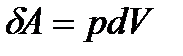 Көлемі
Көлемі  -ден
-ден  -ге дейін өзгергенде газдың жасайтын толық жұмысын интегралдап табамыз:
-ге дейін өзгергенде газдың жасайтын толық жұмысын интегралдап табамыз:  (10.1)
(10.1) . Изохоралық процестің диаграммасы р, V координаталарында ордината осіне параллель түзу болады
. Изохоралық процестің диаграммасы р, V координаталарында ордината осіне параллель түзу болады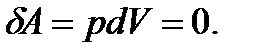
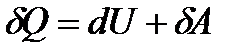 ,
, 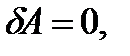
 (10.2)
(10.2)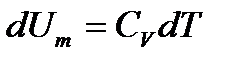 формуласын ескерсек, массасы m газ үшін термодинамиканың I заңының изохоралық процесс үшін жазылуы:
формуласын ескерсек, массасы m газ үшін термодинамиканың I заңының изохоралық процесс үшін жазылуы:
 -ден
-ден 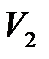 -ге өзгергендегі жасалатын жұмыс
-ге өзгергендегі жасалатын жұмыс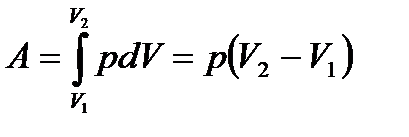
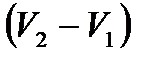 шамасын табамыз:
шамасын табамыз: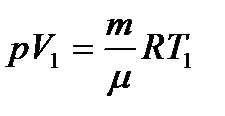 ,
, 


 (10.4)
(10.4) болса, 1 моль газ үшін R=A, демек универсал газ тұрақтысы 1 моль газды 1К температураға дейін қыздыруға жұмсалған изобаралық ұлғаю жұмысына тең. Массасы m газдың изобаралық процесте жылу мөлшері ұлғайғанда,
болса, 1 моль газ үшін R=A, демек универсал газ тұрақтысы 1 моль газды 1К температураға дейін қыздыруға жұмсалған изобаралық ұлғаю жұмысына тең. Массасы m газдың изобаралық процесте жылу мөлшері ұлғайғанда, (10.5)
(10.5)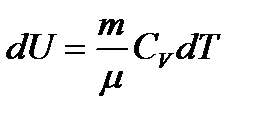 Сонда газ
Сонда газ  - ге тең жұмыс жасайды.
- ге тең жұмыс жасайды. . (10.6)
. (10.6)
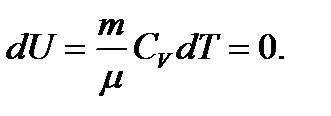
 , (10.7)
, (10.7) (10.8)
(10.8)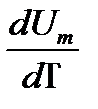 өрнектерін кез-келген m массаға жазып, өрнегін мына түрге келтіреміз: рdV = -
өрнектерін кез-келген m массаға жазып, өрнегін мына түрге келтіреміз: рdV = -  CV dТ.
CV dТ.  = -
= -  = -
= -  .
. = -
= -  + 1,
+ 1,  = - γ
= - γ  өрнегін ламыз. p1 –ден p2 – ге және V1-ден V2-ге дейінгі шектерде интегралдап, содан соң потенцирлеу арқылы
өрнегін ламыз. p1 –ден p2 – ге және V1-ден V2-ге дейінгі шектерде интегралдап, содан соң потенцирлеу арқылы =
=  немесе
немесе  = const теңдеулерін аламыз. Бұл теңдеу адиабаталық процестің теңдеуі болып табылады және Пуассон теңдеуі деп аталады. T, V немесе p, T айнымалыларына көшу үшін Клапейрон – Менделеев теңдеуін пайдаланып, түрлендіреміз:
= const теңдеулерін аламыз. Бұл теңдеу адиабаталық процестің теңдеуі болып табылады және Пуассон теңдеуі деп аталады. T, V немесе p, T айнымалыларына көшу үшін Клапейрон – Менделеев теңдеуін пайдаланып, түрлендіреміз: 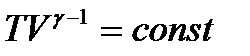 ,
, 
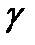 - адиабата көрсеткіші, Пуассон коэффициенті.
- адиабата көрсеткіші, Пуассон коэффициенті.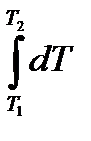 =
= 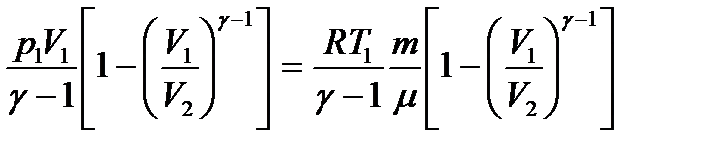 , мұндағы р1 V1=
, мұндағы р1 V1=  - ға, изотермиялық (Т= const) процесте
- ға, изотермиялық (Т= const) процесте  , адиабаталық процесте (Q= const) 0 -ге тең. Жылусыйымдылық тұрақты болатын процестер политропты процесс деп аталады. Термодинамиканың I заңынан жылусыйымдылық тұрақты болған жағдайда С= const политропты процестің теңдеуін алуға болады:
, адиабаталық процесте (Q= const) 0 -ге тең. Жылусыйымдылық тұрақты болатын процестер политропты процесс деп аталады. Термодинамиканың I заңынан жылусыйымдылық тұрақты болған жағдайда С= const политропты процестің теңдеуін алуға болады: (10.11)
(10.11) (10.12)
(10.12) n = 1 – изотермиялық процестің теңдеуі.
n = 1 – изотермиялық процестің теңдеуі. >0, онда цикл сағат тілімен бағыттас жүреді, тура цикл деп аталады. Ал егер цикл ішінде жасалатын жұмыс теріс A =
>0, онда цикл сағат тілімен бағыттас жүреді, тура цикл деп аталады. Ал егер цикл ішінде жасалатын жұмыс теріс A =  (10.13)
(10.13)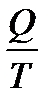 қатынасын келтірілген жылу мөлшері деп атайды. Процестің өте кіші бөлігіндегі келтірілген жылу мөлшері
қатынасын келтірілген жылу мөлшері деп атайды. Процестің өте кіші бөлігіндегі келтірілген жылу мөлшері  ға тең. Кез-келген қайтымды процесс кезінде денеге берілетін келтіріген жылу мөлшері нольге тең:
ға тең. Кез-келген қайтымды процесс кезінде денеге берілетін келтіріген жылу мөлшері нольге тең: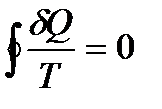 . (10.14)
. (10.14) . (10.15)
. (10.15)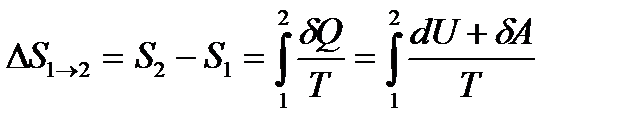 (10.17)
(10.17) , сонда
, сонда , немесе
, немесе (10.18)
(10.18) 1 күйден 2 күйге өткенде процестің қалай өтуіне тәуелсіз екен.
1 күйден 2 күйге өткенде процестің қалай өтуіне тәуелсіз екен. ΔS = 0,
ΔS = 0,  S = const, яғни адиабаталық процесс тұрақты энтропияда өтеді. Сондықтан изоэнтропиялық процесс деп аталады.
S = const, яғни адиабаталық процесс тұрақты энтропияда өтеді. Сондықтан изоэнтропиялық процесс деп аталады.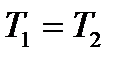 ,
,  (10.19)
(10.19) ,
,  (10.20)
(10.20) (10.21)
(10.21)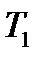 термостаттан- қыздырғыштан цикл кезінде Q1 жылу мөлшері алынады. Температурасы төмен
термостаттан- қыздырғыштан цикл кезінде Q1 жылу мөлшері алынады. Температурасы төмен  термостатқа- салқындатқышқа цикл ішінде Q2 жылу мөлшері беріледі және А = Q1-Q2 жұмыс жасалады. Жылу двигателінің термиялық пайдалы әсер коэффициенті
термостатқа- салқындатқышқа цикл ішінде Q2 жылу мөлшері беріледі және А = Q1-Q2 жұмыс жасалады. Жылу двигателінің термиялық пайдалы әсер коэффициенті 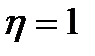 болуы үшін Q2 =0 шарты орындалуы керек, демек жылу двигателінің бір ғана жылу көзі болуы керек, ол мүмкін емес.
болуы үшін Q2 =0 шарты орындалуы керек, демек жылу двигателінің бір ғана жылу көзі болуы керек, ол мүмкін емес. жұмысына тең, газ 1 күйден 2 күйге өткенде:
жұмысына тең, газ 1 күйден 2 күйге өткенде: .
. ішкі энергияның өзгерісі арқылы жасалады.
ішкі энергияның өзгерісі арқылы жасалады. .
.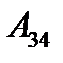
 .
. .
.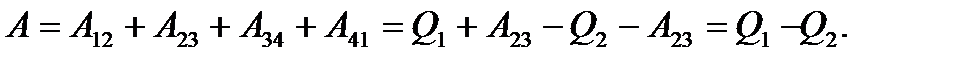
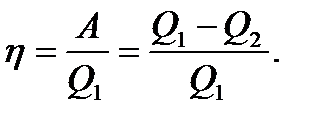

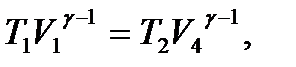
 (10.22)
(10.22) (10.23)
(10.23) және
және 
 Егер қыздырғыштың температурасын 100 К-ге көтеріп, ал суытқыштың температурасын 50 К-ге кемітсек, онда
Егер қыздырғыштың температурасын 100 К-ге көтеріп, ал суытқыштың температурасын 50 К-ге кемітсек, онда 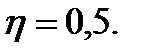 Нақты жылу двигателінің п.ә.к. үйкелістің және жылу жоғалту әсерінен есептелген шамадан кем болады.
Нақты жылу двигателінің п.ә.к. үйкелістің және жылу жоғалту әсерінен есептелген шамадан кем болады. газда қалыпты жағдайдағы молекула саны 2,68
газда қалыпты жағдайдағы молекула саны 2,68  10
10  -не тең, бұл молекулалар 10
-не тең, бұл молекулалар 10  м
м  көлем алады (шамамен молекуланың радиусы 10
көлем алады (шамамен молекуланың радиусы 10  м), оны газдың көлемімен салыстырғанда ескермеуге болады. Ал 500МПа қысымда молекулалардың алатын көлемі газ көлемінің жартысына тең, сондықтан жоғары қысымда және төмен температурада идеал газ моделін нақты газдар үшін қолдануға болмайды.
м), оны газдың көлемімен салыстырғанда ескермеуге болады. Ал 500МПа қысымда молекулалардың алатын көлемі газ көлемінің жартысына тең, сондықтан жоғары қысымда және төмен температурада идеал газ моделін нақты газдар үшін қолдануға болмайды. 10
10  м арақашықтықта білінеді және молекулалар арасындағы арақашықтық өскенде күштің әсері де азаяды. Мұндай күштер жақыннан әсер ету күштері немесе тез әсерлесу күштері деп аталады.
м арақашықтықта білінеді және молекулалар арасындағы арақашықтық өскенде күштің әсері де азаяды. Мұндай күштер жақыннан әсер ету күштері немесе тез әсерлесу күштері деп аталады. мен
мен  алынады.
алынады.  =
=  ) молекулаларды бір-бірінен ажырату үшін тарту күшіне қарсы жасалатын жұмысты анықтайды.
) молекулаларды бір-бірінен ажырату үшін тарту күшіне қарсы жасалатын жұмысты анықтайды.  «
«  қашықтыққа дейін жақындап, қосылуына кедергі жасайды. Егер
қашықтыққа дейін жақындап, қосылуына кедергі жасайды. Егер  »
»  болса, онда зат сұйық күйінде болады, жылулық қозғалыс нәтижесінде молекулалар кеңістікте қозғалып жүреді, орын ауыстырады, бірақ
болса, онда зат сұйық күйінде болады, жылулық қозғалыс нәтижесінде молекулалар кеңістікте қозғалып жүреді, орын ауыстырады, бірақ  (11.1)
(11.1) - молярлық көлем.
- молярлық көлем. (11.2)
(11.2) ,
,  ескере отырып, Ван-дер-Ваальс теңдеуін төмендегідей жазуға болады:
ескере отырып, Ван-дер-Ваальс теңдеуін төмендегідей жазуға болады: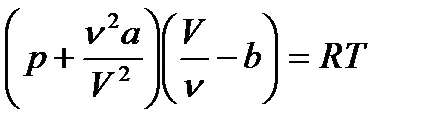 (11.3)
(11.3)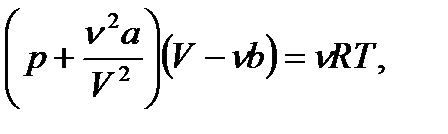 (11.4)
(11.4) ›
›  нақты газдың изотермасы идеал газдың изотермасынан тек азғана формасының қисаюымен ерекшеленетін, монотонды төмен түсетін қисық.
нақты газдың изотермасы идеал газдың изотермасынан тек азғана формасының қисаюымен ерекшеленетін, монотонды төмен түсетін қисық.  болғанда изотерма K нүктесінде ғана бір жерден иіледі. Бұл изотерма
болғанда изотерма K нүктесінде ғана бір жерден иіледі. Бұл изотерма  және қысым
және қысым  да кризистік деп аталады. Кризистік параметрлермен
да кризистік деп аталады. Кризистік параметрлермен 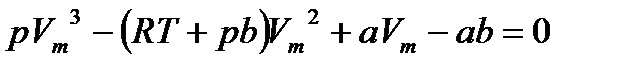 (11.5)
(11.5)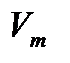 -ге қатысты үшінші дәрежелі теңдеу болып табылады. Демек, бұл теңдеудің үш нақты немесе бір нақты, екі жорамал түбірлері болуы керек және физикалық мағынасы бары тек қана оң нақты түбірлер ғана. Сондықтан бірінші жағдайға төмен температурадағы изотермалар (көлемнің үш мәні
-ге қатысты үшінші дәрежелі теңдеу болып табылады. Демек, бұл теңдеудің үш нақты немесе бір нақты, екі жорамал түбірлері болуы керек және физикалық мағынасы бары тек қана оң нақты түбірлер ғана. Сондықтан бірінші жағдайға төмен температурадағы изотермалар (көлемнің үш мәні  («m» символын ескермейміз) қысымның бір ғана мәніне
(«m» символын ескермейміз) қысымның бір ғана мәніне  жауапты), екіншісіне - жоғары температурадағы изотермалар сәйкес келеді. Изотерманың түрлі бөлігін
жауапты), екіншісіне - жоғары температурадағы изотермалар сәйкес келеді. Изотерманың түрлі бөлігін  жағдайында қарастырайық (11.2-сурет). 1-3 және 5-7 бөліктерінде көлем кемігенде қысым артады. Ал 3-5 бөлігінде газ сығылғанда көлемнің кемуі қысымның да азаюына әкеледі, ал практика табиғатта мұндай күйлердің болмайтынын көрсетеді. 3-5 бөліктің болуы: көлемін біртіндеп өзгерткенде зат барлық уақытта біртекті орта болып қалмайтынын, белгілі уақыттан соң оның күйі секірмелі түрде өзгеріп, зат екі фазаға бөлінетінін көрсетеді. Сондықтан нағыз изотерманың түрі 7-6-2-1 сынықтарымен беріледі. мұндағы 7-6 бөлігі заттың газ тәріздес күйіне, ал 2-1 бөлігі – сұйық күйіне сәйкес келеді. Изотерманың горизонталь 6-2 бөлігіне сәйкес келетін күйлерде заттың сұйық және газ тәріздес фазаларының тепе-теңдігі байқалады.
жағдайында қарастырайық (11.2-сурет). 1-3 және 5-7 бөліктерінде көлем кемігенде қысым артады. Ал 3-5 бөлігінде газ сығылғанда көлемнің кемуі қысымның да азаюына әкеледі, ал практика табиғатта мұндай күйлердің болмайтынын көрсетеді. 3-5 бөліктің болуы: көлемін біртіндеп өзгерткенде зат барлық уақытта біртекті орта болып қалмайтынын, белгілі уақыттан соң оның күйі секірмелі түрде өзгеріп, зат екі фазаға бөлінетінін көрсетеді. Сондықтан нағыз изотерманың түрі 7-6-2-1 сынықтарымен беріледі. мұндағы 7-6 бөлігі заттың газ тәріздес күйіне, ал 2-1 бөлігі – сұйық күйіне сәйкес келеді. Изотерманың горизонталь 6-2 бөлігіне сәйкес келетін күйлерде заттың сұйық және газ тәріздес фазаларының тепе-теңдігі байқалады. (11.6)
(11.6)