 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 4 страница
Үдеудің тангенциал құраушысы
яғни жылдамдық модулынан уақыт бойынша алынған бірінші ретті туындыға тең, жанамаға бағыттас жылдамдықтың өзгеріс шапшаңдығын модулы жағынан сипаттайды. Енді үдеудің екінші құраушысын табайық.
үдеудің нормаль құраушысы деп аталады және қозғалыс траекториясының радиус бойымен центріне бағытталады (сондықтан оны центрге тартқыш үдеу деп те атаймыз). Дененің толық үдеуі тангенциаль және нормаль құраушылардың геометриялық қосындысынан тұрады, яғни Толық үдеудің модулы мынаған тең (1.3-сурет):
1.3-сурет
Тангенциаль және нормаль құраушыларына байланысты үдеудің қозғалысын былай сипаттауға болады: 1. 2. 3. 4. 5. 6. 7. Айналмалы қозғалыс. Қозғалыс кезінде дененің барлық нүктелері шеңберлер сызатын және олардың центрлері айналыс осі деп аталатын бір түзудің бойында жататын қозғалысты айналмалы қозғалыс деп атайды. Айналмалы қозғалысты қарастырғанда бұрыштық жылдамдық және бұрыштық үдеу ұғымдарын енгіземіз. Материалдық нүкте радиусы
Бұрыштық жылдамдықтың өлшем бірлігі:
яғни Бұрыштық жылдамдықтың бағыты оң бұрғанда ережесімен анықталады. Нүктенің шеңбер бойымен толық бір айналым жасауға қажетті уақытын период деп атайды және
1.4-сурет
Нүктенің уақыт бірлігі ішіндегі жасайтын айналым саны периодқа кері шама жиілік деп аталады
Бірлік уақыт ішінде бұрыштық жылдамдықтың өзгерісін сипаттайтын шаманы бұрыштық үдеу
егер Егер қозғалыс үдемелі болса, Материалдық нүктенің ілгерімелі және айналмалы қозғалыстарын сипаттайтын шамалар өзара мынадай қатынаста болады: 1) 2) Айналмалы бірқалыпсыз қозғалыс кезіндегі қозғалыс теңдеулері:
мұндағы
1.5-сурет Бақылау сұрақтары: 1. Материалдық нүкте, санақ жүйесі дегеніміз не? 2. Қандай қозғалысты бірқалыпты ілгерілемелі және айнымалы дейміз? 3. Орташа жылдамдық және орташа үдеу, лездік жылдамдық және лездік үдеулердің анықтамалары мен формулаларын айтыңыздар. 4. Үдеу қандай құраушыларға жіктеледі? Олардың модулі мен бағыттары қалай анықталады? 5. Айналмалы қозғалыс деп қандай қозғалысты айтамыз? Бұрыштық жылдамдық және бұрыштық үдеу дегеніміз не? Бағыттары қандай? 6. Сызықтық және бұрыштық шамалардың арасындағы байланысы қандай? Әдебиеттер: НӘ1,4,6; ҚӘ2,5; ӘН1
№2 дәріс Материялық нүкте динамикасы Ньютон заңдары. Инерциялық санақ жүйелері. Масса және күш. Механикадағы күштер түрлері. Инерциялық емес санақ жүйелері. Гравитациялық күштер. Бүкіл әлемдік тартылыс заңы. Серпімділік күші. Гук заңы. Үйкеліс күштері. Динамика материалдық нүктелердің немесе денелердің әсерлесу кезіндегі қозғалысының өзгерісін зерттейді. Динамикада Ньютонның үш заңы негізгі заңдар болып алынады. Егер қозғалысты санақ жүйесімен байланыстыратын болсақ, онда қозғалушы дене әсер етуші күштен бөлек және санақ жүйесімен байланысты бір қалыпты және түзу сызықты қозғалыста болады. Ньютонның бірінші заңы: материалдық нүктеге (денеге) ешқандай күш әсер етпесе, онда нүкте (дене) өзінің бастапқы тыныштық күйін немесе бір қалыпты, түзу сызықты қозғалысын сақтайды. Материалдық нүктенің немесе денелердің мұндай қасиетін инерциялық деп атайды. Сондықтан да Ньютонның бірінші заңы әдетте инерция заңы аталады. Механикалық қозғалыс салыстырмалы, оның сипаты санақ жүйесіне тәуелді. Ньютонның І заңы барлық санақ жүйлерінде орындалмайды, бұл заң орындалатын санақ жүйелері инерциялды санақ жүйесі деп аталады. Инерциялды санақ жүйесі деп, басқа бір инерциялды санақ жүйесімен салыстырғанда тыныштықта тұратын немесе бірқалыпты және түзу сызықты қозғалытын санақ жүйесін айтамыз. Инерция санақ жүйесіне қатысты үдеумен қозғалатын санақ жүйесі инерциялық емес санақ жүйесі деп аталады. Үдеп ілгерілей қозғалған санақ жүйесінде инерция күші
айналмалы қозғалған санақ жүйесінде тыныш тұрған денеге әсер ететін инерция күші:
айналмалы санақ жүйесінде қозғалған денеге әсер ететін күш:
Инерциялы емес санақ жүйесі үшін динамиканың негізгі заңы:
Күш деп денелердің өзара әсерлесуінің нәтижесінде бір-біріне үдеу беруін айтамыз. Денелердің өзара әсері бір-біріне тек үдеу беріп қоймай, бір-бірінің көлемі мен формасын да өзгерте алады. Демек, дене бөлшектерінің бір-бірімен салыстырғанда орын ауыстыруын дененің деформациясыдеп атайды. Күш – векторлық шама. Дененің жерге тартылуы кезінде оған қарсы әсер ететін екінші денеге түсетін күшті салмақ дейді. Басқа денелер әсер етпегенде, дененің өз жылдамдығын сақтау қабілеті инерттілік деп аталады. Дененің инерттілігін сипаттайтын шама инерттілік массадеп аталады. Материя бір түрден екінші түрге өзгергенде оның массасы мөлшері жағынан тұрақты болып қалады да, оның тек формасы өзгереді. Масса материяның негізгі қасиетін сипаттайтын физикалық скаляр шама, ол инерттіліктің сандық өлшеуіші. Ньютонның екінші заңы ілгерілемелі қозғалыс динамикасының негізгі заңы – ол денелердің өзара әсерлесуі және ілгерімелі қозғалысы кезінде оларда болатын өзгерістерінің байланысын сипаттайды. Егер әр түрлі
Бұл өрнек Ньютонның екінші заңы деп аталады және былай тұжырымдалады: дененің алған үдеуі әсер етуші күшке тура пропорционал, дене массасына кері пропорционал және әсер етуші күштің бағыты бойынша өзгереді. Ньютонның І заңы Ньютонның ІІ заңының дербес түрі болып табылады. Шынында да, тең әсерлі күштің әсері
Күштің өлшем бірлігі –Ньютон, яғни массасы 1 кг денеге 1м/с2 үдеу беру үшін 1Н күшпен әсер ету керек. Ньютонның екінші заңын басқа түрде де жазып көрсетуге болады. Ол үшін кинематика бөліміндегі үдеудің мұндағы дененің (материалдық нүктенің) массасының классикалық физикада тұрақтылығын ескеріп, оны дифференциалдық астына жазуға болады:
Бұл қозғалыс теңдеуі Ньютонның екінші заңын дифференциал түрде көрсетеді. Ал дифференциалдың астындағы дененің массасы мен жылдамдығының көбейтіндісі дененің импульсі немесе қозғалыс мөлшері деп аталатын векторлық шаманы береді: Импульс ұғымын пайдаланып, Ньютонның екінші заңын жалпы түрде жазуға және тұжырымдауға болады:
Дененің (материалдық нүктенің) импульсінің немесе қозғалыс мөлшерінің уақыт бойынша бірінші туындысы оған әсер етуші күшке тең. Денелердің немесе материалдық нүктелердің арасындағы әсерлесу Ньютонның үшінші заңымен анықталады. Ньютонның үшінші заңы оның екінші заңын толықтыра түседі және денелердің қозғалыс күйлерін өзгеріске ұшырататын өзара әсер екендігін көрсетеді. Бұл заң былай тұжырымдалады: әсерлесуші екі дененің бір-біріне әсері әруақытта сан жағынан тең, бағыттары жағынан қарама-қарсы болады. Мысалы: массалары Ньютонның үшінші заңы бойынша:
Бұдан Үйкеліс және серпімділік күштері.Механикалық процесстерде денелерге әртүрлі күштер әсер етеді: тартылыс, үйкеліс, серпімділік. Денелердің өзара салыстырмалы қозғалысы кезінде олардың жанасу беттері арасында пайда болатын күштерді үйкеліс күштері деп атайды. Денелердің жанасу беттерінің арасында сұйық немесе газ қабаты болмаған жағдайда үйкеліс сырғанау және домалау үйкелістері болып екіге бөлінеді. Сырғанау үйкеліс күші
мұндағы
2.1-сурет Жазықтықта дене жатса және оған Сырғанаудан басқа домалау үйкелісі де болады. Ол кезде үйкеліс азырақ болады, домалау үйкеліс күші нормаль қысым күшіне тура пропорционал және дөңгелектің қисықтық радиусына кері пропорционал болады:
мұндағы
Поиск по сайту: |
 1.2-сурет
1.2-сурет (1.7)
(1.7) нүктесі
нүктесі  нүктесіне орын ауыстырып,
нүктесіне орын ауыстырып,  доғасына тең элементар жол жүреді.
доғасына тең элементар жол жүреді.  уақыт аралығы өте аз болғандықтан
уақыт аралығы өте аз болғандықтан  доғасының
доғасының  хордасынан айырмашылығы аз болады. Онда
хордасынан айырмашылығы аз болады. Онда  және
және  үшбұрыштарының ұқсастығынан
үшбұрыштарының ұқсастығынан  шығады. Ал
шығады. Ал  , онда
, онда  .
.  шегінен,
шегінен,  аламыз.
аламыз.  мен
мен  векторының арасындағы
векторының арасындағы 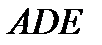 бұрышы тік бұрышқа ұмтылады. Бұдан
бұрышы тік бұрышқа ұмтылады. Бұдан  ,
,  және
және 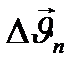 векторлары өзара перпендикуляр болады. Жылдамдық векторы
векторлары өзара перпендикуляр болады. Жылдамдық векторы  қозғалыс траекториясына жанамаға бағытталғандықтан,
қозғалыс траекториясына жанамаға бағытталғандықтан,  векторы жанамаға перпендикуляр бағытталады да, жылдамдықтың бағыты бойынша өзгерісін сипаттайды. Үдеудің екінші құраушысы
векторы жанамаға перпендикуляр бағытталады да, жылдамдықтың бағыты бойынша өзгерісін сипаттайды. Үдеудің екінші құраушысы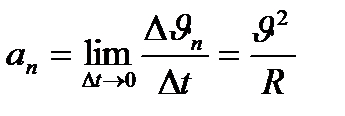 (1.8)
(1.8)
 (1.9)
(1.9)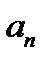



 – бірқалыпты түзу сызықты қозғалыс,
– бірқалыпты түзу сызықты қозғалыс, – бірқалыпты айнымалы қозғалыс,
– бірқалыпты айнымалы қозғалыс, – үдеуі айнымалы түзу сызықты қозғалыс,
– үдеуі айнымалы түзу сызықты қозғалыс, – шеңбер бойымен қозғалыс,
– шеңбер бойымен қозғалыс, – бірқалыпты қисық сызықты қозғалыс,
– бірқалыпты қисық сызықты қозғалыс, – қисық сызықты айнымалы қозғалыс,
– қисық сызықты айнымалы қозғалыс, –үдеуі айнымалы қисық сызықты қозғалыс.
–үдеуі айнымалы қисық сызықты қозғалыс.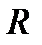 шеңбер бойымен қозғалып,
шеңбер бойымен қозғалып,  уақыт мезетінде
уақыт мезетінде  бұрышына бұрылсын. Бұрыштық жылдамдық
бұрышына бұрылсын. Бұрыштық жылдамдық  деп, дененің бұрылу бұрышынан уақыт бойынша алынған бірінші ретті туындысына тең физикалық векторлық шаманы айтады.
деп, дененің бұрылу бұрышынан уақыт бойынша алынған бірінші ретті туындысына тең физикалық векторлық шаманы айтады. (1.10)
(1.10) . Сызықтық жылдамдық пен бұрыштық жылдамдықтың арасындағы байланысты 1.4 суреттен көруге болады:
. Сызықтық жылдамдық пен бұрыштық жылдамдықтың арасындағы байланысты 1.4 суреттен көруге болады:
 (1.11)
(1.11) әріпімен белгілейді.
әріпімен белгілейді.



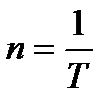 . Нүкте шеңбер бойымен бір қалыпты қозғалып, бір периодқа тең уақыт аралығында
. Нүкте шеңбер бойымен бір қалыпты қозғалып, бір периодқа тең уақыт аралығында  толық бір айналым
толық бір айналым  жасайды, яғни
жасайды, яғни  -ға орын ауыстырады. Осыдан
-ға орын ауыстырады. Осыдан 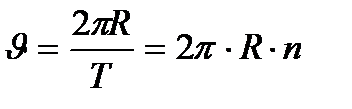 . Екі қатынасты салыстырудан алатынымыз:
. Екі қатынасты салыстырудан алатынымыз: (1.12)
(1.12) деп атап, оны математикалық түрде былай жазады:
деп атап, оны математикалық түрде былай жазады:  Айналыс бір қалыпты болмаған кезде берілген уақыт мезетіндегі бұрыштық үдеу мынаған тең:
Айналыс бір қалыпты болмаған кезде берілген уақыт мезетіндегі бұрыштық үдеу мынаған тең: (1.13)
(1.13) екендігін ескерсек, онда
екендігін ескерсек, онда  болады, яғни айналмалы қозғалыстың бұрыштық үдеуі бұрыштық жылдамдықтан уақыт бойынша алынған бірінші ретті, ал бұрылу бұрышының екінші ретті туындысына тең болады. Бұрыштық үдеу векторлық шама оның бағыты бұрыштық жылдамдықтыңбағытымен бағыттас, өлшем бірлігі
болады, яғни айналмалы қозғалыстың бұрыштық үдеуі бұрыштық жылдамдықтан уақыт бойынша алынған бірінші ретті, ал бұрылу бұрышының екінші ретті туындысына тең болады. Бұрыштық үдеу векторлық шама оның бағыты бұрыштық жылдамдықтыңбағытымен бағыттас, өлшем бірлігі  болады.
болады. векторы мен
векторы мен  векторы бағыттас болады, егер кемімелі болса
векторы бағыттас болады, егер кемімелі болса  векторы мен
векторы мен 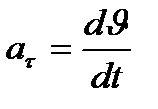 , бұдан
, бұдан  немесе
немесе 
 немесе
немесе  .
. ,
,  (1.14)
(1.14) бастапқы бұрыштық жылдамдық.
бастапқы бұрыштық жылдамдық.


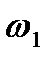





 (2.1)
(2.1) - инерциялы емес санақ жүйесінің үдеуі;
- инерциялы емес санақ жүйесінің үдеуі; (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4)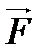 күштерінің қандай да тек
күштерінің қандай да тек  массалы бір денеге әсерін қарастырсақ, онда ол дененің алатын
массалы бір денеге әсерін қарастырсақ, онда ол дененің алатын  үдеуі осы әсер ететін күштерге тура пропорционал болады:
үдеуі осы әсер ететін күштерге тура пропорционал болады:  . Егер әр түрлі
. Егер әр түрлі  үдеулері әр түрлі болады. Дене массасы үлкен болған сайын, ол дененің үдеуі азырақ болады: яғни
үдеулері әр түрлі болады. Дене массасы үлкен болған сайын, ол дененің үдеуі азырақ болады: яғни  ,
,  . Осы өрнектерді пайланып, әрі күш пен үдеудің векторлық шамалар екенін ескере отырып, былай жазуға болады:
. Осы өрнектерді пайланып, әрі күш пен үдеудің векторлық шамалар екенін ескере отырып, былай жазуға болады: (2.5)
(2.5) болған жағдайда (денеге сыртттан басқа дененің әсері болмаған жағдайда) оның үдеуі де
болған жағдайда (денеге сыртттан басқа дененің әсері болмаған жағдайда) оның үдеуі де 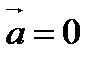 болады. Ал біз үдеудің
болады. Ал біз үдеудің  екенін білеміз, осыдан
екенін білеміз, осыдан  екені шығады. Дене өзінің бастапқы тыныштық немесе бір қалыпты түзу сызықты қозғалыс күйін сақтайды, яғни инерция заңына айналады. Тағы бір ескеретін жай денеге бір мезгілде бірнеше күш әсер етсе, онда үдеу осы күштердің векторлық қосындысына тең қорытқы
екені шығады. Дене өзінің бастапқы тыныштық немесе бір қалыпты түзу сызықты қозғалыс күйін сақтайды, яғни инерция заңына айналады. Тағы бір ескеретін жай денеге бір мезгілде бірнеше күш әсер етсе, онда үдеу осы күштердің векторлық қосындысына тең қорытқы  . (2.6)
. (2.6)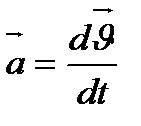 мәнін ескеретін болсақ, онда
мәнін ескеретін болсақ, онда 
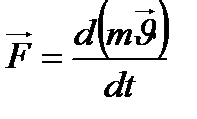 (2.7)
(2.7)
 (2.8)
(2.8) және
және  екі дене алып қарастырайық. Олар
екі дене алып қарастырайық. Олар  және
және  күштерінің күштерінің әсерінен
күштерінің күштерінің әсерінен  ,
, 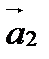 үдеу алады. Ньютонның екінші заңы бойынша:
үдеу алады. Ньютонның екінші заңы бойынша:  .
. (2.9)
(2.9)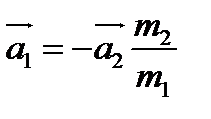 әсерлесуші екі дененің үдеулері олардың массаларына кері пропорционал әрі қарама-қарсы бағытта бағытталады. Мұндағы
әсерлесуші екі дененің үдеулері олардың массаларына кері пропорционал әрі қарама-қарсы бағытта бағытталады. Мұндағы 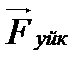 әрдайым денелердің жанасу бетінің бойымен орын ауыстыруға қарама-қарсы бағытталады. Сондықтан үйкеліс күші әрқашан денелердің салыстырмалы қозғалыс жылдамдығының модулын кемітуге тырысады. Тыныштық үйкеліс күші денелердің жанасу бетіне жанама бойымен бағытталған сыртқы
әрдайым денелердің жанасу бетінің бойымен орын ауыстыруға қарама-қарсы бағытталады. Сондықтан үйкеліс күші әрқашан денелердің салыстырмалы қозғалыс жылдамдығының модулын кемітуге тырысады. Тыныштық үйкеліс күші денелердің жанасу бетіне жанама бойымен бағытталған сыртқы 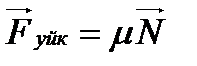 (2.10)
(2.10) -үйкеліс коэффициенті, ол жанасатын беттердің материалына, өңдеу сапасына тәуелді.
-үйкеліс коэффициенті, ол жанасатын беттердің материалына, өңдеу сапасына тәуелді.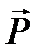


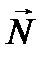
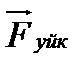 күшінен көп болса ғана қозғалысқа келеді. Тыныштық максимал үйкеліс күші сондай-ақ сырғанау үйкеліс күші үйкелетін беттердің жанасу беттерінің шамасына тәуелді болмайды және үйкелісетін беттерді бір-біріне қысатын, қалыпты қысым күші
күшінен көп болса ғана қозғалысқа келеді. Тыныштық максимал үйкеліс күші сондай-ақ сырғанау үйкеліс күші үйкелетін беттердің жанасу беттерінің шамасына тәуелді болмайды және үйкелісетін беттерді бір-біріне қысатын, қалыпты қысым күші  шамасына пропорционал болады.
шамасына пропорционал болады. (2.10а)
(2.10а) - дөңгелектің қисықтық радиусы.
- дөңгелектің қисықтық радиусы.