 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 6 страница
Онда немесе
мұндағы Сонымен механикалық жүйенің қозғалыс мөлшерінің уақыт бойынша туындысы жүйеге әсер ететін сыртқы күштердің геометриялық қосындысына тең. Қарастырып отырған жүйеміздің тұйық екенін ескерсек, онда сыртқы күштер әсері нөлге тең болады, яғни:
бұдан Бұл өрнек қозғалыс мөлшерінің сақталу заңы болып табылады: тұйық жүйенің қозғалыс мөлщері сақталады, яғни уақыт өтуімен өзгермейді. Қозғалыс мөлшерінің сақталу заңы тек қана классикалық физикада ғана емес сонымен қатар тұйық жүйедегі өте ұсақ бөлшектер үшін де орындалады (кванттық механика заңы үшін). Сондықтан бұл заң табиғаттың негізгі заңдарының бірі болып табылады. Табиғатта жұмыс істелу салдарынан материя қозғалысының формасы бір түрден екінші түрге өзгеріп отырады. Материалдық объектінің бір күйден екінші күйге көшкенде жұмыс істеу қабілетін энергия деп атайды. Дененің механикалық қозғалысының өзгерісі сол денеге басқа денелердің әсер күшінен пайда болады. Әсерлесетін денелердің арасындағы энергия алмасу процесінің сандық мөлшерін сипаттау үшін күш жұмысы деген ұғым енгіземіз. Дене түзу сызықпен қозғалған жағдайда оған орын ауыстыру бағытына
Біз дененің қандай да бір М нүктеден N нүктеге орын ауыстыруын қарастырайық. Орын ауыстыру MN қисық сызықты себебі денеге түсірілген күш айнымалы. Айнымалы күштің жұмысы, жолдың аз бөлігіндегі элементар жұмыстардың қосындысына тең. Жолды шексіз элементар бөліктерге бөлгендегі жұмыс интегралмен анықталады. Мұндағы интегралды есептеу үшін
3.1.сурет Бұл формуладан: егер Істелінген жұмыстың жылдамдығын сипаттау үшін қуат деген ұғым енгіземіз. Қуат деп, жұмыстан уақыт бойынша алынған бірінші ретті туындыға тең шаманы айтады. Қуаттың өлшемі – ватт (Вт):
Материя қозғалысы формасының әртүрлі болуына байланысты энергия да әртүрлі болады: механикалық, ішкі, электромагниттік, ядролық т.б. Соның ішінде механикалық энергияны қарастырайық. Механикалық энергияның өзі кинетикалық және потенциалдық болып екіге бөлінеді. Кинетикалық энергия деген ұғымды еркін денеге әсер етуші күштің жұмысын есептеу арқылы түсіндірген жөн. Түсірілген күштің істеген жұмысы дененің жылдамдығының өзгертеді. Бұл байланыс материалдық нүктенің кинетикалық энергиясы деп аталатын физикалық шама арқылы өрнектеледі. Материалдық дененің кинетикалық энергиясын анықтау керек болсын. Сонда массасы Сонымен Дененің орнына ғана байланысты болатын күштер үшін олардың денеге қатысты істейтін жұмысы жолға тәуелді болмай, дененің кеңістіктегі бастапқы және соңғы орнымен ғана анықталатын жағдайы болады. Бұл жағдайдағы күштерді консервативті күштер деп атаймыз. Консервативті күші бар өрісті потенциалды деп атайды. Егер күш жұмысы дененің бір нүктеден екінші бір нүктеге орын ауыстыру траекториясына тәуелді болса, ондай күштер диссипативті күштер деп аталады (мысалы, үйкеліс күші). Потенциалдық энергия ұғымы консервативті күштердің жұмысына байланысты енгізіледі. Ауырлық күші өрісінде істелген жұмыс жолдың формасына және ұзындығына байланысты емес, тек жолдың соңғы нүктесінің бастапқы нүктесіне қарағанда қаншама биік жатқандығына байланысты. Потенциалдық энергияның абсолют мәні өлшенбейді, бірақ әруақытта нақты тұрақты мәніне дейінгі дәлдікпен бағаланатынын түсіну өте маңызды. Мысал үшін серіппенің потенциалық энергиясын табайық. Гук заңы бойынша серпімділік күші деформацияға пропорционал: Енді
Енді бұл теңдеулерді қосатын болсақ:
бұдан бірінші қосылғыш жүйенің кинетикалық энергиясының өсімшесін береді: ал екінші қосылғыш барлық күштердің жүйедегі денелерді яғни бұдан жүйенің толық энергиясы:
Сонымен, тек консервативті күштер әсер еткенде ғана тұйық жүйенің толық энергиясы тұрақты болады, яғни уақыт өтуімен өзгермейді. Бұл тұжырымдалған қағида механикалық энергияның сақталу заңы деп аталады және механикалық негізгі заңдарының маңызы салдарының бірі болып табылады. Энергияның сақталу заңын кеңірек түсіну мынаны көрсетеді: энергия жоғалып кетпейді және жоқтан пайда болмайды, ол тек бір түрден екінші түрге ауысады және де энергияның бір түрі қаншаға кемісе, екінші түрі соншаға артады. Басқаша айтқанда, материя және қозғалыс біртұтас байланыста болады. Материясыз қозғалыс, қозғалыссыз материя болмайды. Қозғалыс – материяның өмір сүру формасы. Бақылау сұрақтары: 1. Қандай жағдайда жұмыс істелінеді? 2. Жұмыстың істелу шапшаңдығын қандай шама сипаттайды? 3. Импульстің сақталу заңының тұжырымдалуы және оның математикалық теңдеуі. Ол не себептен табиғаттың фундаменталды заңы болады? 4. Механикалық энергияның формуласын өрнектеп шығарыңдар. 5. Потенциалдық энергияның өзгерісі немен байланысты? 6. Механикалық энергияның сақталу заңы қандай жүйеде орындалады? 7. Энергияның сақталу және түрлену заңының физикалық мәні неде? Не себептен ол табиғаттың фундаменталды заңы болады? Әдебиеттер: НӘ1,4,6; ҚӘ2,5; ӘН1 №4 дәріс Қатты дене динамикасы Абсолют қатты дене ұғымы. Қатты дененің күш моменті және инерция моменті. Штейнер теоремасы. Импульс моменті. Импульстің сақталу заңы табиғаттың іргелі заңы екендігі. Қатты дененің қозғалмайтын оське қатысты айналмалы қозғалыс динамикасының теңдеуі. Қатты дененің инерция моменті.Жалпы өмірде кездесетін қатты денелер, күштің әсерінен деформацияланады, яғни олардың өлшемі мен формасы өзгереді. Көбінесе деформациясының шамалы болатындығы сондайлық, дененің қозғалысын сипаттағанда оны елемеуге де болады. Сондықтан біз әрі қарай осы тақырыпты қарастырғанда абсолют қатты дене деген түсінік енгіземіз. Қандай жағдайда да дененің деформациясын елемеуге болатын немесе барлық жағдайда осы дененің екі нүктесінің (яғни екі бөлшегінің) ара қашықтығы өзгермей сақталатын денелерді абсолют қатты денелер деп айтамыз. Айналмалы қозғалыс кезінде қатты денелердің барлық нүктелері шеңбер бойымен қозғалады, олардың центрлері айналу осі деп аталатын бір түзудің бойында жатады. Айналмалы қозғалысты сипаттау үшін кеңістіктегі айналу осінің қалпын және әрбір уақыт мезетіндегі дененің бұрыштық жылдамдығын білу керек. Қатты дененің айналысын қарастырған кезде инерция моменті деген ұғым енгіземіз. Қатты дененің немесе материалдық нүктенің айналу осіне қатысты инерция моменті деп дененің немесе материалдық нүктенің
4.1-сурет Қатты дененің өзі жеке-жеке материалық нүктелер жиынтығынан тұрады. Сондықтан қатты денені (4.1-сурет) материалық нүктелер жиынтығы ретінде де қарастыруға болады. Жүйенің (дененің) айналу осіне қатысты инерция моменті деп осы жүйені құрайтын Мысал: Біртекті тұтас цилиндрдің инерция моментін табайық. 4.2-суретте цилиндр биіктігін
4.2-сурет Қарастырылып отырған элементар цилиндрдің көлемі: Сонда тұтас цилиндрдің инерция моменті:
бұдан
Поиск по сайту: |

 ,
, - жүйенің қозғалыс мөлшері.
- жүйенің қозғалыс мөлшері. немесе
немесе 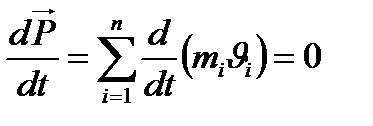
 (3.5)
(3.5) α бұрыш жасай,
α бұрыш жасай, 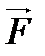 тұрақты күш әсер етсе, онда бұл күштің жұмысы күштің орын ауыстыру бағытына түсірілген құраушысы мен күш түскен нүктенің орын ауыстыруының көбейтіндісіне тең:
тұрақты күш әсер етсе, онда бұл күштің жұмысы күштің орын ауыстыру бағытына түсірілген құраушысы мен күш түскен нүктенің орын ауыстыруының көбейтіндісіне тең: 
 - әсер еткен күштің жолдың бағытына түсірілген проекциясы.
- әсер еткен күштің жолдың бағытына түсірілген проекциясы.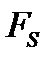 күшінің
күшінің  жолға
жолға  траектория бойымен байланысын қарастырамыз. Жұмыстың графигі штрихталған фигураның ауданымен сипатталады. Егер
траектория бойымен байланысын қарастырамыз. Жұмыстың графигі штрихталған фигураның ауданымен сипатталады. Егер  және
және  болса, онда жұмыс:
болса, онда жұмыс: (3.6)
(3.6)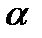



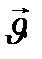
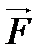 пен
пен  арасындағы бұрыш
арасындағы бұрыш  болса, онда
болса, онда  құраушысы қозғалыс жылдамдық векторымен бағыттас болады да, күш жұмысы оң болады, егер
құраушысы қозғалыс жылдамдық векторымен бағыттас болады да, күш жұмысы оң болады, егер  болса, онда
болса, онда  болса, онда күш жұмысы нөлге тең болады. Жұмыстың өлшем бірлігі:
болса, онда күш жұмысы нөлге тең болады. Жұмыстың өлшем бірлігі:  күш әсерінен дене
күш әсерінен дене  орын ауыстырса
орын ауыстырса  жұмыс жасалады.
жұмыс жасалады.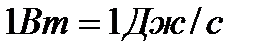 . Егер дене әсер еткен күштің салдарынан тұрақты жылдамдықпен қозғалса, онда қуат былай анықталады:
. Егер дене әсер еткен күштің салдарынан тұрақты жылдамдықпен қозғалса, онда қуат былай анықталады: (3.7)
(3.7) дененің жылдамдығы
дененің жылдамдығы 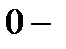 ден
ден  -ға дейін артқан кездегі күштің істеген жұмысы, сол дененің кинетикалық энергиясының өсуіне жұмсалады, яғни
-ға дейін артқан кездегі күштің істеген жұмысы, сол дененің кинетикалық энергиясының өсуіне жұмсалады, яғни  . Әсер етуші күшке Ньютонның екінші заңын пайдаланамыз
. Әсер етуші күшке Ньютонның екінші заңын пайдаланамыз  . Осы инерция күшінің нәтижесінен дене
. Осы инерция күшінің нәтижесінен дене 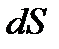 -ке орын ауыстырса, онда істелінген жұмыс
-ке орын ауыстырса, онда істелінген жұмыс  болады, яғни
болады, яғни  . Бұдан
. Бұдан  , сонда
, сонда  Енді істелген жұмысты табу үшін соңғы өрнекті интегралдаймыз, яғни
Енді істелген жұмысты табу үшін соңғы өрнекті интегралдаймыз, яғни 
 күшінің істелінген жұмысы кинетикалық энергия деп аталатын
күшінің істелінген жұмысы кинетикалық энергия деп аталатын  шамаға тең болады. Соңғы формуладан кинетикалық энергияның дененің тек қана массасы мен жылдамдығына тәуелді екендігін көреміз, яғни жүйенің кинетикалық энергиясы оның қозғалысының күй функциясы болып табылады. Потенциалдық энергия жүйенің бөлшектерінің өзара орналасуымен және олардың сыртқы күштік өрістегі орнына байланысты анықталады. Егер дене кеңістіктің әрбір нүктесінде басқа бір дененің күш әсеріне тап болатын болса және нүктеден нүктеге өзгеретін жағдайға түссе, онда ол денені күштер өрісінде тұр деп айта аламыз.
шамаға тең болады. Соңғы формуладан кинетикалық энергияның дененің тек қана массасы мен жылдамдығына тәуелді екендігін көреміз, яғни жүйенің кинетикалық энергиясы оның қозғалысының күй функциясы болып табылады. Потенциалдық энергия жүйенің бөлшектерінің өзара орналасуымен және олардың сыртқы күштік өрістегі орнына байланысты анықталады. Егер дене кеңістіктің әрбір нүктесінде басқа бір дененің күш әсеріне тап болатын болса және нүктеден нүктеге өзгеретін жағдайға түссе, онда ол денені күштер өрісінде тұр деп айта аламыз. функциясының нақты түрі күш өрісінің сипатына тәуелді. Айталық, мысалы материалдық дене ауырлық күшінің біртекті өрісінде қозғалғанда, яғни дене бір деңгейден екінші деңгейге көтерілгенде жұмыс істеуі салдарынан потенциалдық энергиясы өзгереді. Массасы
функциясының нақты түрі күш өрісінің сипатына тәуелді. Айталық, мысалы материалдық дене ауырлық күшінің біртекті өрісінде қозғалғанда, яғни дене бір деңгейден екінші деңгейге көтерілгенде жұмыс істеуі салдарынан потенциалдық энергиясы өзгереді. Массасы  биіктікке көтерілген кезде істеген жұмысы потенциалдық энергияның өзгерісіне тең:
биіктікке көтерілген кезде істеген жұмысы потенциалдық энергияның өзгерісіне тең: 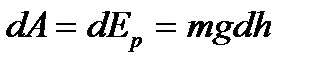 . Толық жұмысты табу үшін жер бетінен, яғни
. Толық жұмысты табу үшін жер бетінен, яғни  ден
ден  биікткке дейін интегралдаймыз:
биікткке дейін интегралдаймыз: 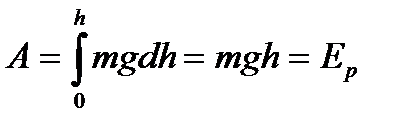
 , мұндағы
, мұндағы  серпімділік (қатаңдық) коэффициенті. Ньютонның үшінші заңы бойынша
серпімділік (қатаңдық) коэффициенті. Ньютонның үшінші заңы бойынша 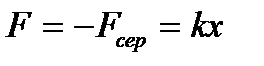 . Элементар
. Элементар  деформацияланғанда күштің істейтін элементар жұмысы
деформацияланғанда күштің істейтін элементар жұмысы 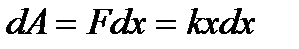 , ал толық жұмыс серппенің потенциалдық энергиясының өсуіне жұмсалады:
, ал толық жұмыс серппенің потенциалдық энергиясының өсуіне жұмсалады: 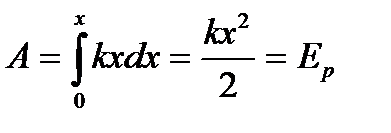
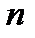 материалдық нүктелер жиынынан тұратын оңашаланған жүйені қарастырайық,оларға сыртқы және консервативті ішкі күштер әсер ететін. Материалдық нүктелер жүйесінің массалары
материалдық нүктелер жиынынан тұратын оңашаланған жүйені қарастырайық,оларға сыртқы және консервативті ішкі күштер әсер ететін. Материалдық нүктелер жүйесінің массалары  , жылдамдықтары
, жылдамдықтары  деп, ал
деп, ал  осы материалдық нүктелердің әрқайсысына әсер ететін консервативті ішкі күштер,
осы материалдық нүктелердің әрқайсысына әсер ететін консервативті ішкі күштер,  жүйеге әсер ететін сыртқы күштер деп алайық. Осы күштердің әсерінен жүйедегі нүктелер
жүйеге әсер ететін сыртқы күштер деп алайық. Осы күштердің әсерінен жүйедегі нүктелер 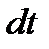 уақыт аралығында
уақыт аралығында 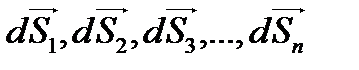 элементар ара қашықтыққа орын ауыстырсын. Теңдіктің екі жағын да осы
элементар ара қашықтыққа орын ауыстырсын. Теңдіктің екі жағын да осы  көбейтіп, әрі
көбейтіп, әрі  ескерсек, онда:
ескерсек, онда:

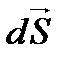 элементар орын ауыстыру үшін істелген жұмысы, яғни теріс “-“ таңбалы потенциялық энергияның өсімшесіне тең:
элементар орын ауыстыру үшін істелген жұмысы, яғни теріс “-“ таңбалы потенциялық энергияның өсімшесіне тең: 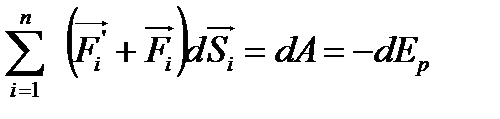

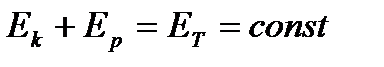 (3.8)
(3.8) квадратының көбейтіндісіне тең физикалық шаманы айтады:
квадратының көбейтіндісіне тең физикалық шаманы айтады: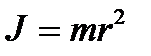 (4.1)
(4.1)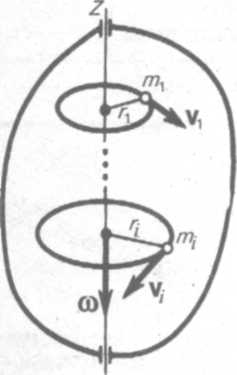
 . Массасы бірқалыпты таралған дене үшін бұл сумма барлық көлемі бойынша интегралданады:
. Массасы бірқалыпты таралған дене үшін бұл сумма барлық көлемі бойынша интегралданады: 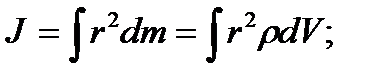 мұндағы
мұндағы 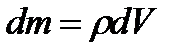 .
. , ал оның радиусын
, ал оның радиусын 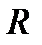 деп алайық. Цилиндрді кішкене бөліктерге бөлеміз, қалыңдығы
деп алайық. Цилиндрді кішкене бөліктерге бөлеміз, қалыңдығы  тең. Оның ішкі радиусы r, ал сыртқы радиусы
тең. Оның ішкі радиусы r, ал сыртқы радиусы  тең. Әрбір кішкене цилиндірдің инерция моменті
тең. Әрбір кішкене цилиндірдің инерция моменті  , мұндағы
, мұндағы 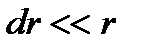 ескереміз, ал
ескереміз, ал  -барлық элементар цилиндрдің массасы.
-барлық элементар цилиндрдің массасы.
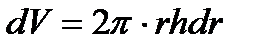 , егер
, егер  - материалдың тығыздығы болса, онда
- материалдың тығыздығы болса, онда  яғни
яғни  оның массасы, ал
оның массасы, ал 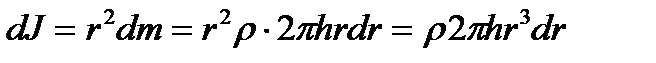 элементар инерция моменті болады.
элементар инерция моменті болады. ,
, -цилиндрдің көлемі, ал
-цилиндрдің көлемі, ал  оның массасы болады. Сонда цилиндрдің инерция моменті:
оның массасы болады. Сонда цилиндрдің инерция моменті: