 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 3 страница
7.2 СӨЖ бойынша тапсырмаларды орындаудың мерзімі және тақырыптық жоспары
2. ПӘННІҢ ОҚУ - ӘДІСТЕМЕЛІК ҚАМТЫЛУ КАРТАСЫ Оқу пәні: Физика Кафедра: Жалпы техникалық пәндер Мамандық: Қоршаған ортаны қорғау және өмір тіршілігінің қауіпсіздігі Оқыту формасы: Күндізгі Күндізгі: 1,2 курс 2,3 семестр
Пән бойынша жалпы сағат саны 270 сағат, соның ішінде дәріс 30 сағат, практикалық сабақтар(семинарлар) 30 сағат, лабораториялық сабақтар 30 сағат, СӨЖ 135 сағат, СМӨЖ 45 сағат.
3. ДӘРІС КЕШЕНІ: Семестр №1 дәріс Кинематика негіздері. Кіріспе. Механикалық қозғалыс. Материялық нүкте түсінігі. Кеңістік және уақыт. Санақ жүйесі. Материялық нүкте қозғалысын кинематикалық сипаттау. Қозғалыс заңы. Траектория теңдеуі. Жылдамдық және үдеу. Айналмалы қозғалыс кинематикасының элементтері. Қисық сызықты қозғалыс кезіндегі жылдамдық пен үдеу. Бұрыштық жылдамдық, бұрыштық үдеу. Физика – өріс пен заттың жалпы қасиеттері мен олардың қозғалыс заңдылықтарын зерттейтін ғылым. Физика – табиғат жөніндегі жетекші ғылымдардың бірі. Табаиғатты зерттейтін басқа ғылымдардан оның шекарасын ажыратып, бөліп алу мүмкін емес. Демокрит, Аристотель, Архимед тәрізді ерте дүниедегі ұлы ойшылдардың ғылымға қосқан теңдесі жоқ мол үлесі халықтың ғасырлар бойына жинақталған тәжірибелерімен ұштаса келіп, физиканың ірге тасы болып саналатын классикалық механиканың тууына себеп болды. Бұл тәжірибелерді қорытып, математикалық жүйеге келтірген Ньютон мен Галилей еді. Ньютон мен Галилей, Ломоносов пен Фарадей, Максвелл сияқты көптеген ғылым алыптарының еңбектері бір арнаға қосылып, классикалық физиканы жасады. XIX ғасырдың соңғы жылдарында ашылған атом құрлысының күрделігін растайтын тәжірибелер, жарық табиғатын түсіндірудегі қайшылықтар классикалық физика тұрғысынан шешуін таппайтын проблемалар еді. Неміс физигі М. Планк осылардың ішінен абсолют қара дене проблемасын талдай отырып, алғаш рет квант идеясын ұсынды. Ол заттың сәуле түрінде энергия шығарып, энергия жұтуы үздіксіз құбылыс емес, қайта үздікті құбылыс деп санады. Сәулені зат энергия үлестері түрінде (квант түрінде) ғана шығарады деп ұйғарды. Планк идеясын түрлі қайшылықтарынан арылтып, әрі қарай дамытқан Эйнштейн, Гейзенберг, Дирак және Шредингерлер болды. Олар квант теориясын математикалық жүйеге келтіріп, барлық табиғат құбылыстарына қолдануға болатындай дәрежеге жеткізді. Осы квант теориясымен қатар ашылған Эйнштейннің салыстырмалық теориясы материя қозғалысы және сол қозғалысқа қатысты физиканың ең терең ұғымдары – кеңістік пен уақыт – жөніндегі ғасырлар бойы қалыптасқан көзқарасты негізінен өзгертті. Салыстырмалық теориясы жарық жылдамдығымен шамалас жылдамдықпен қозғалған денелерге Ньютон механикасының ықпалы жүрмейтіндігін көрсетті. Тек жылдамдығы төмен дене қозғалысы Ньютон заңдарына көнеді. Сонымен, Эйнштейн теориясы ғасырлар бойы қалыптасқан физиканың заңдылықтарын ғылым бетінен сыпырып тастаған жоқ. Қайта оның түрлі құбылыстарда қолданылу шекарасын ашып берді. Өзімізді қоршаған табиғаттың неден тұратынын анықтау – сонау ерте дүниеден бастап, әлі күнге дейін өзінің шешімін таппай келе жатқан мәселе. Демокрит дүниенің ең қарапайым «кірпіші» - әрі қарай бөлінбейтін бөлшек – атом деп санады. Бірақ атомның да протон, нейтрон және электрон тәрізді элементар бөлшектерден тұратыны белгілі болды. Мұндай бөлшектердің саны көбейіп кеткендіктен оларды жүйеге келтіру қолға алынды. Бұл бөлшектерге берілген «элементар» деген аттың өзі де, оның әрі қарай бөлінбейтін қарапайымдылығында болуы керек. Қазіргі физиканың ең басты проблемаларының бірі болып саналатын термоядролық реакциялар – болашақтағы энергияның сарқылмас көзі болмақ. Механика – бұл механикалық қозғалыстарды және оның болу немесе өзгеру себептерін қарастыратын физиканың бір бөлімі. Механика үш бөлімге бөлінеді: 1) кинематикаға, 2) динамикаға, 3) статикаға. Кинематика – дене қозғалысын қамтамасыз ететін себептерге байланыссыз қозғалысты оқып зерттейді, динамика –қозғалыстың сол немесе басқадай сипатын қамтамасыз ететін себептерге байланысты денелердің қозғалысын оқып зерттейді, ал статика – денелердің тепе-теңдіктегі шартын зерттейді. Уақыт өтуіне байланысты денелердің кеңістікте орын ауыстыруын механикада қозғалыс деп атайды. Механикалық қозғалыстың ең қарапайым мысалы ретінде материалық нүкте қозғалысын қарастыруға болады. Материалдық нүкте деп массасы қарастырылып отырған дененің массасына тең, берілген есептің шартында өлшемін елемеуге болатын денені айтады. Материалдық нүкте орнын қандай-да бір болмасын кез-келген денеге, яғни санақ денесіне қатысты анықтауға болады. Кез-келген таңдап алынған нүкте тыныштықта тұр деп аламыз, ал соған қатысты кез-келген координат жүйесін кеңістіктік санақ жүйесі деп атайды. Кеңістіктік санақ жүйесіндегі әрбір нүктенің орны
және
(1.1) және (1.1а) теңдеулер материалдық нүктенің кинематикалық теңдеулері деп аталады. Материялдық нүктенің қозғалысы кезінде артында із қалдыруын оның траекториясы деп атайды. Траекторияның формасына қарай түзу сызықты және қисық сызықты деп екіге бөлуге болады. Материалдық нүкте қозғалысын траекториямен беттестіре сызсақ,
Бірқалыпты қозғалыс. Егер қозғалған дене кез-келген өзара тең уақыт аралығында бірдей жол жүрсе, ондай қозғалысты бірқалыпты түзу сызықты қозғалыс деп атайды. Қозғалыс түрліше болуы мүмкін, мысалы әр түрлі дене бірдей уақыт аралығында әр түрлі жол жүреді, қозғалыстың осындай өзгерісін біз Бірқалыпты қозғалыс теңдеуі:
Бірқалыпсыз қозғалыс. Айнымалы қозғалыс кезінде бірдей уақыт аралығында материалдық нүктенің жүрген жолдары бірдей болмайды. Мұндай жағдайда қозғалыстың орташа жылдамдығы деген ұғым енгізуіміз керек. Орташа жылдамдық векторы деп нүктенің радиус- векторының өсімшесінің осы уақыт аралығына қатынасын айтамыз:
Материалдық нүктенің берілген уақыт мезетіндегі қозғалысын лездік жылдамдық арқылы сипаттайды. Лездік жылдамдық
 уақыт аралығы азайған сайын уақыт аралығы азайған сайын  жүрілген жолы жүрілген жолы  орын ауыстыруға жақындап беттеседі. орын ауыстыруға жақындап беттеседі.
Сонда уақыттың кез-келген мезетіндегі қозғалыс жылдамдығы деп, жүрілген жолдың уақыт бойынша алынған бірінші ретті туындысын айтамыз.
бұдан
Бірқалыпсыз қозғалыс кезінде біз уақыт өтуіне байланысты жылдамдықтың қалай өзгеретіндігін қарастырамыз. Егер қозғалыс жылдамдығы ұдайы артып отырса, үдемелі қозғалыс деп, егер жылдамдығы ұдайы кеміп отырса, онда кемімелі қозғалыс деп атайды. Олай болса уақытқа байланысты жылдамдықтың қаншалықты тез өзгеретіндігін сипаттайтын үдеу деген физикалық шаманы енгіземіз. Бірқалыпсыз қозғалыстың үдеуі дегеніміз жылдамдықтың өсімшесіне тура пропорционал және осы өсімше пайда болған уақыт өсімшесіне кері пропорционал шама:
Бұл жағдайда қозғалыс айнымалы болғандықтан жылдамдық өсімшесінің өзгеруіне сәйкес үдеу де өзгерісте болады, олай болса орташа үдеу деген ұғым енгізуге тура келеді:
Демек, үдеу шама жағынан жылдамдықтың уақыт бойынша алынған бірінші ретті туындысы, ал жүрілген жолдың уақыт бойынша алынған екінші ретті туындысына тең:
Үдеу қозғалыс жылдамдығын саны жағынан да, бағыты жағынан да сипаттайтын, векторлық шама, өлшем бірлігі:
Дененің қисық сызық бойымен қозғалысы. Бастапқы
Поиск по сайту: |
 координаттарымен анықталады. Осы үш координаттың орнына
координаттарымен анықталады. Осы үш координаттың орнына  радиус-векторды алуға болады. Радиус-вектор деп координаттар басынан қарастырылып отырған нүктеге дейінгі бағытталған кесіндіні айтады. Қозғалысты сипаттау үшін кеңістіктік санақ жүйесі жеткіліксіз болып саналады. Сондықтан қозғалысты тек кеңістік –уақыт санақ жүйесінде ғана толық сипаттауға болады. Уақыт өзгерісіне байланысты материалдық нүкте қозғалысы мына теңдеумен беріледі:
радиус-векторды алуға болады. Радиус-вектор деп координаттар басынан қарастырылып отырған нүктеге дейінгі бағытталған кесіндіні айтады. Қозғалысты сипаттау үшін кеңістіктік санақ жүйесі жеткіліксіз болып саналады. Сондықтан қозғалысты тек кеңістік –уақыт санақ жүйесінде ғана толық сипаттауға болады. Уақыт өзгерісіне байланысты материалдық нүкте қозғалысы мына теңдеумен беріледі:
 (1.1)
(1.1)
 (1.1а)
(1.1а) траектория ұзындығын материалдық нүктенің жүрген жолы деп атайды, 1.1-суретте көрсетілген. Оны
траектория ұзындығын материалдық нүктенің жүрген жолы деп атайды, 1.1-суретте көрсетілген. Оны  әрпімен белгілейді, жүрілген жол скаляр шама
әрпімен белгілейді, жүрілген жол скаляр шама  .
.  -бастапқы мезеттен соңғы уақыт мезетіне дейінгі ара қашықтық
-бастапқы мезеттен соңғы уақыт мезетіне дейінгі ара қашықтық  , орын ауыстыру деп аталады. Ол - векторлық шама. Егер траектория түзу сызықты болса, онда жүрілген жол мен орын ауыстыру беттеседі. Дене түзу бойымен қозғалса, қозғалыс түзу сызықты деп аталады.
, орын ауыстыру деп аталады. Ол - векторлық шама. Егер траектория түзу сызықты болса, онда жүрілген жол мен орын ауыстыру беттеседі. Дене түзу бойымен қозғалса, қозғалыс түзу сызықты деп аталады. 1.1-сурет
1.1-сурет жылдамдық деген ұғым енгізу арқылы сипаттаймыз. Жылдамдық-векторлық шама, ол траекторияға жүргізілген жанама бойымен бағытталады. Қозғалыстың жылдамдығы жүрілген жолға тура пропорционал, сол жолды жүруге кеткен уақытқа кері пропорционал:
жылдамдық деген ұғым енгізу арқылы сипаттаймыз. Жылдамдық-векторлық шама, ол траекторияға жүргізілген жанама бойымен бағытталады. Қозғалыстың жылдамдығы жүрілген жолға тура пропорционал, сол жолды жүруге кеткен уақытқа кері пропорционал:  , өлшем бірлігі
, өлшем бірлігі  .
.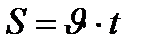 (1.2)
(1.2) (1.3)
(1.3) уақыт аралығы шексіз кемігендегі орташа жылдамдық ұмтылатын шекке тең:
уақыт аралығы шексіз кемігендегі орташа жылдамдық ұмтылатын шекке тең: (1.3а)
(1.3а) (1.4)
(1.4) .
. 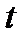 - дан
- дан  шектерінде интегралдап жүрілген жолдың ұзындығын анықтаймыз :
шектерінде интегралдап жүрілген жолдың ұзындығын анықтаймыз : 
 (1.4а)
(1.4а)
 . Орташа үдеу алынып отырған
. Орташа үдеу алынып отырған  уақыт аралығы шексіз кемігенде, сол орташа үдеудің ұмтылатын шегін лездік үдеу деп атайды.
уақыт аралығы шексіз кемігенде, сол орташа үдеудің ұмтылатын шегін лездік үдеу деп атайды.
 (1.5)
(1.5) . Бастапқы уақыт мезетінде қозғалыс жылдамдығы
. Бастапқы уақыт мезетінде қозғалыс жылдамдығы  , ал
, ал  болсын, онда қозғалыс үдеуі
болсын, онда қозғалыс үдеуі 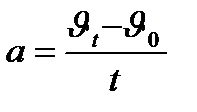 болады. Қозғалыстың кез-келген уақыт мезетіндегі жылдамдығы:
болады. Қозғалыстың кез-келген уақыт мезетіндегі жылдамдығы: 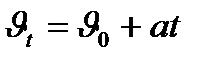 . Олай болса бірқалыпты айнымалы қозғалыс теңдеуін шығарып алуға болады:
. Олай болса бірқалыпты айнымалы қозғалыс теңдеуін шығарып алуға болады: , яғни
, яғни  (1.6)
(1.6) уақыт мезетіеде 1.2 суретте
уақыт мезетіеде 1.2 суретте  нүктесінің жылдамдығы
нүктесінің жылдамдығы  болсын. Қозғалыстағы нүкте
болсын. Қозғалыстағы нүкте 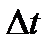 уақытта
уақытта  нүктесіне көшіп,
нүктесіне көшіп,  жылдамдығынан бағыты жағынан да, модулы жағынан да өзгеше
жылдамдығынан бағыты жағынан да, модулы жағынан да өзгеше 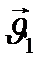 жылдамдыққа ие болады:
жылдамдыққа ие болады: 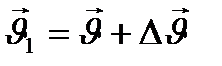 . Енді
. Енді  векторын
векторын  табамыз.
табамыз.  векторын екі құраушыға жіктеуге болады. Ол үшін
векторын екі құраушыға жіктеуге болады. Ол үшін  нүктесінен жылдамдық бағытымен бағыттас, модулы жағынан
нүктесінен жылдамдық бағытымен бағыттас, модулы жағынан  векторына тең
векторына тең  векторын жүргіземіз. Бұдан
векторын жүргіземіз. Бұдан  векторы шамасы жағынан
векторы шамасы жағынан  -ға тең,
-ға тең,  уақыт аралығында жылдамдық өзгерісін модулы жағынан сипаттайды:
уақыт аралығында жылдамдық өзгерісін модулы жағынан сипаттайды:  . Екінші құраушы вектор
. Екінші құраушы вектор  ,
,  уақыт аралығында жылдамдық өзгерісін бағыты жағынан сипаттайды.
уақыт аралығында жылдамдық өзгерісін бағыты жағынан сипаттайды.