 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 7 страница
Бұдан басқа кейбір денелердің иерция моменттері: 1. Радиусы
2. Ұзындығы
3. Ұзындығы
Егер айналатын қатты дененің ауырлық центрі арқылы өтетін оське айланысты инерция моменті
Айналыстың кинетикалық энегиясы. Абсолют қатты дененің қозғалмайтын Бірақ біздің қарастырып отырғанымыз абсолют қатты дене болғандықтан, оның қозғалысының бұрыштық жылдамдығы бірдей болады:
Дененің айналмалы қозғалысының кинетикалық энергиясы оның жеке бөліктерінің кинетикалық энергиясынан құралады:
бұған енді
Сонымен, қозғалмайтын остьтен айналатын дененің кинетикалық энергиясы деп, осы оськеқатысты инерция моменті мен бұрыштық жылдамдықтың квадратының көбейтіндісінің жартысына тең шаманы айтады. Бұл өрнек ілгерімелі қозғалатын дененің
мұндағы: Қатты дененің күш моменті. Қозғалмайтын 0 нүктесіне байланысты күш моменті деп, 0 нүктесінен
М
4.3-сурет Мұндағы мұндағы Енді осы денені айналдырған кездегі жұмыстың өрнегін анықтайық (4.4-сурет). Айналмайтын 0 осьтен
4.4-сурет Денеміз абсолют қатты дене болғандықтан, осы айналдырушы күш жұмысы осы дененің түгел бұрылуына жұмсалған жұмысына тең. Дене өте азғантай dφ бұрышқа бұрылған кезде, В нүктесі dS жол жүреді: dS=rdφ. Бұрылған кездегі істелген жұмыс бұрылу бағытына түсірілген күш проекциясы мен бұрылу шамасының көбейтіндісіне тең:
яғни денені айналдырғандағы істелінген жұмыс әсер етуші күш моменті мен бұрылу бұрышының көбейтіндісіне тең. Денені айналдырғанда істелінген жұмыс оның кинетикалық энергиясының өсуіне жұмсалады: бірақ
Денеге әсер етуші күш моменті дененің инерция моменті мен бұрыштық үдеуінің көбейтіндісіне тең: Қатты дененің импульс моменті және оның сақталуы. Айналмалы қозғалыс пен ілгерімелі қозғалысты салыстырайық, яғни дененің импульсінің аналогы қандай шама болатынын қарастырайық. 0 қозғалмайтын оське қатысты А материалдық нүктенің импульс моменті
мұндағы
мұндағы r sinα = l – 0 нүктесіне қатысты Енді кез-келген і нүктесінің немесе mi дене бөлшегінің массасының қозғалмайтын оське қатысты импульс моментін
Ал қозғалмайтын оське қатысты абсолют қатты дененің импульс моменті әрбір жеке бөлшектерінің импульс моменттерінің суммасына тең:
Бізге бұрыннан белгілі
яғни Сонымен, қозғалмайтын оське қатысты қатты дененің импульс моменті осы оське қатысты дененің инерция моменті мен бұрыштық жылдамдықтың көбейтіндісіне тең. Соңғы өрнекті уақыт бойынша дифференциалдасақ:
яғни Бұл өрнек қатты дененің айналмалы қозғалыс динамикасының тағы бір түрін береді. Қозғалмайтын оське қатысты қатты дененің импульс моментінің уақыт мезетіндегі өзгерісі осы оське қатысты күш моментіне тең болады. Егер біз тұйық жүйе алсақ, онда сыртқы күш моменті
Соңғы өрнек импульс моментінің сақталу заңын береді: тұйық жүйенің импульс моменті сақталады, яғни уақыт өтуімен өзгермейді. Импульс моментінің сақталу заңы табиғаттың фундаменталды заңы. Ол кеңістіктің белгілі бір симметриялық қасиетімен байланысты, кеңістіктің изотроптығымен байланысты, яғни координаталар санақ жүйесінде таңдап алынған ось бағытына қатысты физикалық заңдылықтардың инварианттылығына байланысты. Импульс моментінің сақталуын үйкеліссіз вертикаль осьтен айналатын Жуковский орындығына адамды тұрғызып көрсетуге болады (4.5-сурет).
4.5-сурет Бақылау сұрақтары: 1. Абсолютті қатты дененің инерция моменті деген не және айналмалы қозғалысты инерция моментінің орны қандай? 2. Штейнер теоремасын түсіндіру және тұжырымдау. 3. Қозғалмайтын ось арқылы айналатын дененің кинетикалық энергиясының формуласы қандай және оны қалай өрнектеуге болады? 4. Қатты дененің айналмалы қозғалыс динамикасының теңдеуін өрнектеу және тұжырымдау. 5. Қатты дененің, материалдық нүктенің импульс моменті деген не? Импульс моментінің вектор бағыты қалай анықталады? 6. Импульс моментінің сақталу заңы. Әдебиеттер: НӘ1,4,6; ҚӘ2,5; ӘН1 №5 дәріс Арнайы салыстырмалылық теориясының элементтері Салыстырмалылықтың механикалық принципі. Галилей түрлендірулері. Эйнштейн постулаттары. Лоренц түрлендірулері. Түрлендірудің инварианттары. Жылдамдықтарды қосудың релятивтік заңы. Импульс пен энергияны релятивтік түрлендіру. Салыстырмалылықтың механикалық принципі. Галилей түрлендірулері. Егер санақ жүйелері бір-бірімен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалса және олардың біреуінде Ньютонның динамика заңдары орындалатын болса, онда бұл жүйелер инерциалдық санақ жүйелері болып табылады. Барлық инерциалдық санақ жүйелерінде классикалық динамика заңдары бірдей формада болады, салыстырмалылық принципінің негізі осында (Галилейдің салыстырмалылық принципі). Дәлелдеу үшін 2 санақ жүйесін қарастырайық: қозғалмайтын инерциалдық жүйе К (координаттары х,у,z) және К жүйесіне қатысты түзу сызықтың бойымен бірқалыпты
5.1-сурет
Бұл теңдеуді координаталар осіне проекциялары арқылы жазуға болады.
бұл теңдеулерді Галилей түрлендірулері деп атайды. Дененің бір инерциалдық санақ жүйесіндегі координаталары мен ол жүйемен салыстырғанда бір қалыпты және түзу сызықты қозғалыстағы екінші инерциалдық жүйедегі координаталарын байланыстыратын қатынастарды Галилей түрлендірулері деп атайды. Егер Классикалық механикада уақыт санақ жүйелерінің салыстырмалылық қозғалысына тәуелсіз, сондықтан жоғарыдағы түрлендіруге тағы да бір теңдеу қосуға болады: Жазылған қатынастардың бәрі тек қана классикалық механика ( (5.1)-теңдеуді уақыт бойынша дифференциалдайтын болсақ, классикалық мехакниканың жылдамдықтарын қосу заңын аламыз:
К санақ жүйесінде үдеу Сонымен, бір-бірімен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалатын К және К
Демек, егер (5.5)-теңдеуден салыстырмалылықтың механикалық принципінің дәләлдемесі шығады; динамика заңдары бір инерциалдық санақ жүйесінен екіншісіне көшкенде өзгермейді, яғни координаталар түрлендірулеріне қатысты инвариантты болып табылады. Бұл Галилейдің қорытындысы. Эйнштейн постулаттары. Санақ жүйесінде жүргізілетін бірде бір механикалық тәжірибемен, оның тыныштықта немесе бірқалыпты түзу сызықты қозғалыста екенін анықтау мүмкін емес. XIX ғасырдың соңында зарядталған бөлшектердің қатты жүрісін зерттегенде, олардың қозғалысы классикалық механиканың тұжырымдарымен қайшы келетіндігі анықталды. Мысалы, жарықтың таралуы немесе электромагнит толқындарының Максвелл анықтаған теңдеулері механика теориясына қайшы болды. Осындай қайшылықтарды шешу үшін жаңа механиканы құруға тура келді. Бұл жұмыс тек қана А.Эйнштейннің қолынан келді, яғни ол арнайы салыстырмалылық теориясының негізін салды. Арнайы салыстырмалылық теориясының негізін тұжырымдаған Эйнштейн мынадай екі постулат ұсынды: І постулат: берілген жүйенің тыныш тұрғандығын немесе тұрақты жылдамдықпен қозғалып бара жатқандығын сол жүйенің ішінде жасалған тәжірибе арқылы біліп болмайды. Басқаша айтқанда, қандай тәсілдер қолданғанымен абсолют қозғалысты анықтау мүмкін емес. ІІ постулат: жарықтың вакуумдағы жылдамдығы барлық инерциялдық санақ жүйесінде бірдей және тұрақты шама болады. Басқаша айтқанда, жарық жылдамдығы жарық көзі мен бақылаушы қозғалысына тәуелді емес. Эйнштейннің бірінші постулаты әдетте салыстырмалылық принципі, ал екінші постулаты – жарық жылдамдығының тұрақтылық принципі деп аталады. Эйнштейннің осы теоремасы ХХ ғасырда өрбіген ең маңызды физикалық теориялардың бірі болып табылады. Лоренц түрлендірулері. Эйнштейн постулаттарын негізге ала отырып, инерциалдық санақ жүйелеріндегі құбылыстарға талдау жасау арқылы классикалық Галилей түрлендірулерінің оларға қайшы екендігін және басқа түрлендірулермен ауыстырылуы тиістігін көрсетті. Енді қысқаша соған тоқталайық. Екі инерциалдық санақ жүйелерін қарастырайық; К (координаталары х,у,z) және К жүйесіне қатысты х осі бойымен
Поиск по сайту: |
 (4.2)
(4.2)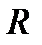 болатын шардың центрі арқылы өтетін оське қатысты инерция моменті:
болатын шардың центрі арқылы өтетін оське қатысты инерция моменті: (4.3)
(4.3) стерженге перпендикуляр әрі оның ортасы арқылы өтетін оське қатысты инерция моменті:
стерженге перпендикуляр әрі оның ортасы арқылы өтетін оське қатысты инерция моменті: (4.4)
(4.4) (4.5)
(4.5) белгілі болса, онда оның кез-келген осы оське параллель осьтен айналғандағы инерция моменті Штейнер теоремасы арқылы анықталады: кез-келген оське қатысты инерция моменті – берілген оське параллель және дене инерциясының центрі арқылы өтетін оське қатысты
белгілі болса, онда оның кез-келген осы оське параллель осьтен айналғандағы инерция моменті Штейнер теоремасы арқылы анықталады: кез-келген оське қатысты инерция моменті – берілген оське параллель және дене инерциясының центрі арқылы өтетін оське қатысты  массасының осьтер арасындағы
массасының осьтер арасындағы  арақашықтығының квадратына көбейтіндісінің қосындысына тең:
арақашықтығының квадратына көбейтіндісінің қосындысына тең: (4.6)
(4.6) осьтен айналысын қарастырайық. Осы денені ойша кішкене көлемшелерге бөлейік, оның массалары
осьтен айналысын қарастырайық. Осы денені ойша кішкене көлемшелерге бөлейік, оның массалары  айналмайтын осьтен
айналмайтын осьтен  қашықта болсын. Қатты денелердің оське қатысты айналысында
қашықта болсын. Қатты денелердің оське қатысты айналысында  массалары әр түрлі
массалары әр түрлі  радиусты шеңберлер сыза қозғалып,
радиусты шеңберлер сыза қозғалып,  сызықтық жылдамдыққа ие болады.
сызықтық жылдамдыққа ие болады. (4.7)
(4.7)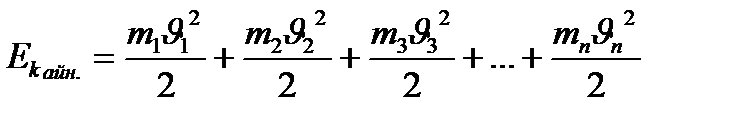 немесе
немесе 
 i=riω өрнегін пайдалансақ:
i=riω өрнегін пайдалансақ: (4.8)
(4.8)
 кинетикалық энергиясына ұқсас келеді. Айналмалы қозғалыс кезінде
кинетикалық энергиясына ұқсас келеді. Айналмалы қозғалыс кезінде  инерция моменті, ал
инерция моменті, ал  сызықтық жылдамдық рөлін ω бұрыштық жылдамдық атқарады. Көлбеу жазықтықтан домалап келе жатқан дененің, мысалы цилиндрдің, кинетикалық энергиясы ілгерімелі қозғалыс энергиясы мен айналмалы қозғалыс энергиясының қосындысынан тұрады:
сызықтық жылдамдық рөлін ω бұрыштық жылдамдық атқарады. Көлбеу жазықтықтан домалап келе жатқан дененің, мысалы цилиндрдің, кинетикалық энергиясы ілгерімелі қозғалыс энергиясы мен айналмалы қозғалыс энергиясының қосындысынан тұрады: (4.9)
(4.9) – дененің массалар центрінің сызықтық жылдамдығы, ω-дененің бұрыштық жылдамдығы,
– дененің массалар центрінің сызықтық жылдамдығы, ω-дененің бұрыштық жылдамдығы,  нүктесіне жүргізілген радиус-вектор
нүктесіне жүргізілген радиус-вектор  векторы мен оған түскен
векторы мен оған түскен 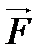 күшінің көбейтіндісіне тең физикалық шаманы айтады:
күшінің көбейтіндісіне тең физикалық шаманы айтады: 

 псевдовектор, 4.3-суретте оның бағыты
псевдовектор, 4.3-суретте оның бағыты  (4.10)
(4.10) бұрышы
бұрышы 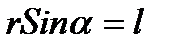 r – бұл 0 нүктесі мен әсер етуші күш сызығының арасындағы ең қысқа арақашықтық күш иіні деп аталады. Сонда
r – бұл 0 нүктесі мен әсер етуші күш сызығының арасындағы ең қысқа арақашықтық күш иіні деп аталады. Сонда 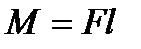 күш моменті айналдырушы күш
күш моменті айналдырушы күш  нүктесіне
нүктесіне  -ға тең.
-ға тең. dS
r
dS
r
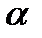

 F
F
 , мұндағы
, мұндағы  , сонда
, сонда  . Бізге бұрыннан r sinα = l иінді береді, ал
. Бізге бұрыннан r sinα = l иінді береді, ал  күш моментін береді. Сондықтан
күш моментін береді. Сондықтан (4.11)
(4.11) ,
,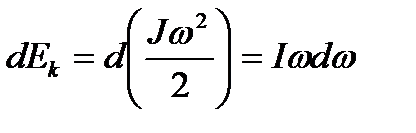 , сондықтан
, сондықтан  немесе
немесе 
 ескере отырып, мына өрнекті аламыз:
ескере отырып, мына өрнекті аламыз: ; (4.12)
; (4.12) – қозғалмайтын оське қатысты қатты дененің айналмалы қозғалысының динамикалық теңдеуін береді.
– қозғалмайтын оське қатысты қатты дененің айналмалы қозғалысының динамикалық теңдеуін береді. және
және  векторлардың көбейтіндісімен анықталатын физикалық шама болып табылады:
векторлардың көбейтіндісімен анықталатын физикалық шама болып табылады: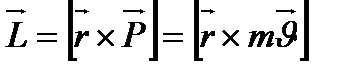
 нүктесіне жүргізілген радиус – вектор,
нүктесіне жүргізілген радиус – вектор, 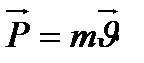 - материалдық нүктенің импульсі немесе қозғалыс мөлшері.
- материалдық нүктенің импульсі немесе қозғалыс мөлшері. - псевдовектор, оның бағытын оң бұрғанда ережесімен
- псевдовектор, оның бағытын оң бұрғанда ережесімен  -ға айналдыра бұрғанда ілгерімелі қозғалысының бағытымен бағыттас болады. Импульс моментінің модулі:
-ға айналдыра бұрғанда ілгерімелі қозғалысының бағытымен бағыттас болады. Импульс моментінің модулі:
 векторының иіні, ал α -
векторының иіні, ал α -  векторларының арасындағы бұрыш. Импульс моменті
векторларының арасындағы бұрыш. Импульс моменті 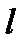 иін мен материалдық нүктенің импульсінің
иін мен материалдық нүктенің импульсінің  көбейтіндісіне тең.
көбейтіндісіне тең. анықтаймыз. Абсолют қатты денені қозғалмайтын оське қатысты айналдыра қоссақ, онда осы дененің әрбір жеке нүктесі осы оське қатысты тұрақты ri радиуспен және
анықтаймыз. Абсолют қатты денені қозғалмайтын оське қатысты айналдыра қоссақ, онда осы дененің әрбір жеке нүктесі осы оське қатысты тұрақты ri радиуспен және 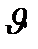 i сызықтық жылдамдықпен шеңбер сыза қозғалады.
i сызықтық жылдамдықпен шеңбер сыза қозғалады.  жылдамдығы мен mі
жылдамдығы мен mі  импульсі осы радиусқа перпендикуляр бағытталған, яғни радиус
импульсі осы радиусқа перпендикуляр бағытталған, яғни радиус  осы
осы 
 (4.13)
(4.13)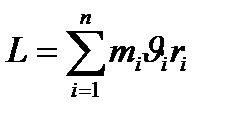
 пайдалана отырып, былай жазамыз:
пайдалана отырып, былай жазамыз:
 (4.14)
(4.14)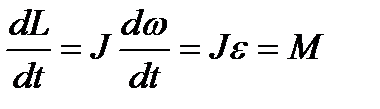
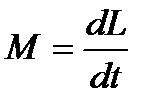 (4.15)
(4.15)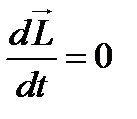 , олай болса
, олай болса 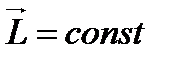 (4.16)
(4.16) көбейсе, ω азаяды немесе
көбейсе, ω азаяды немесе 
 (
(  ) жылдамдықпен қозғалатын K
) жылдамдықпен қозғалатын K  жүйесі. Бастапқы
жүйесі. Бастапқы  мезетте екі жүйенің координаталарының бастары дәлме-дәл келіп тұрған болсын. Кез-келген
мезетте екі жүйенің координаталарының бастары дәлме-дәл келіп тұрған болсын. Кез-келген  уақыт мезетіндегі бұл жүйелердің бір-біріне қатысты орналасуы суретте көрсетілгендей болсын. Жылдамдық
уақыт мезетіндегі бұл жүйелердің бір-біріне қатысты орналасуы суретте көрсетілгендей болсын. Жылдамдық  ОО
ОО  . Екі жүйедегі
. Екі жүйедегі  нүктесінің координаталарының өзара байланыстын табамыз. 5.1-суреттен
нүктесінің координаталарының өзара байланыстын табамыз. 5.1-суреттен (5.1)
(5.1)
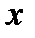
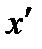





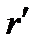
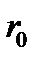

 (5.2)
(5.2)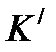 жүйесі К жүйесіне қатысты
жүйесі К жүйесіне қатысты  осі бойымен
осі бойымен 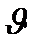 жылдамдықпен қозғалатын болса (бастапқы уақыт мезетінде координаталар осі беттессін), онда координаталарды Галилейше түрлендіру мына түрде жазылады:
жылдамдықпен қозғалатын болса (бастапқы уақыт мезетінде координаталар осі беттессін), онда координаталарды Галилейше түрлендіру мына түрде жазылады: 

 (5.3)
(5.3) ) тұрғысынан қарағанда орындалады, ал жарық жылдамдығына жақын жылдамдықтар үшін Галилей түрлендіруі жалпы Лоренц түрлендірулерімен алмастырылады.
) тұрғысынан қарағанда орындалады, ал жарық жылдамдығына жақын жылдамдықтар үшін Галилей түрлендіруі жалпы Лоренц түрлендірулерімен алмастырылады. (5.4)
(5.4)
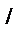 жүйелерінде,
жүйелерінде,  (5.5)
(5.5)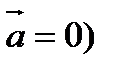 , онда берілген теңдеуге сәйкес
, онда берілген теңдеуге сәйкес 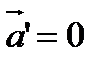 , яғни К
, яғни К  жүйесі инерциалды (нүкте онымен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалады немесе тыныштық қалпын сақтайды).
жүйесі инерциалды (нүкте онымен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалады немесе тыныштық қалпын сақтайды). жылдамдықпен қозғалатын К
жылдамдықпен қозғалатын К