 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 5 страница
Серпімділік күші. Сыртқы күштердің әсерінен дененің немесе оның жеке бөліктерінің пішінінің өзгерісі деформация деп аталады. Деформация кезінде пайда болатын және өзара әсерлесетін дене бөлшектерінің орын ауыстыруына қарсы жаққа бағытталатын күшті серпімділік күші деп атайды. Серпімділік күшін Гук заңы арқылы анықтауға болады. Бұл заң серпімді деформацияның созылу, сығылу, ығысу, бұралу, иілу сияқты түрлері үшін орындалады. Дененің серпімді деформациясы кезінде пайда болатын серпімділік күші дененің ұзаруына пропорционал да, дене бөліктерінің орын ауыстыру бағытына қарама-қарсы бағытталады:
мұндағы Мысалы: қозғалмайтын
Бүкіләлемдік тартылыс заңы. Кеплер аспан денелерінің қозғалысын зерттеп, бүкіл әлемдік тартылыс заңын ашты. Ол былай тұжырымдалады: кез-келген екі материалдық нүктенің (дененің) арасындағы өзара әсер тартылыс күші, осы нүктелердің (денелердің) массаларына тура пропорционал, ал олардың арақашықтығының квадратына кері пропорционал болады:
мұндағы Әрқайсысының массасы 2.2-сурет
Ауырлық күші. Жерге жақын орналасқын кез-келген денеге жердің тарту күші әсер етеді, осы күштің әсерінен Ньютонның екінші заңы бойынша дене еркін түсу үдеуімен
Физиканың фундаментальды заңына сүйене, дененің салмағы тартылыс өрісінде бірдей үдеумен құлайды, оны дененің еркін түсу удеуі деп атайды. Практикалық есептер шығарғанда мәнін Егер жердің өз осінен айналуын (суточное вращение) ескермесек, онда ауырлық күші мен гравитациялық тартылыс күші бір-біріне өзара тең болады:
Мұндағы
ауырлық күші жер бетінен алыстаған сайын азаяды. Салмақ және салмақсыздық. Физикада дененің салмағы
Сонда дененің салмағы Тартылыс өрісі және оның кернеулігі.Ньютонның тартылыс заңы әсерлесуші тартылыс күші дене массалары мен олардың ара қашықтығына байланысты анықталады, бірақ ол әсерлесу қалай жүреді оны көрсетпейді. Тартылыс күші әсерлесуші денелердің қандай ортада тұрғанына байланыссыз, тартылыс вакуумде де өмір сүреді. Материалдық нүктелердің (денелердің) арасында әсерлесу осы денелер айналасында пайда болатын тартылыс өрісі немесе гравитациялық өріс арқылы беріледі. Бұл өріс те материяның өмір сүруінің бір түрі. Тартылыс өрісінің негізгі қасиеті: осы өріске енген кез-келген
мұндағы
2.3-сурет 2.4-сурет Кернеулік тартылыс өрісінің күштік сипаттамасы береді. Егер кернеулік барлық нүктеде бірдей болса, онда тартылыс өрісі біртекті деп аталады. Егер кернеулік векторы өрісінің барлық нүктесінде А нүктесін кесіп өтетін түзудің бойымен бағытталса, онда ол тартылыс өрісі орталық деп аталады (2.4-сурет). Тартылыс өрісіндегі жұмыс. Тартылыс өрісіндегі потенциал. Тартылыс өрісіндегі күштің әсерінен
Осы денені
мұндағы минус таңбасы, бұл жағдайда әсер етуші тартылыс күші мен орын ауыстырудың қарама-қарсы бағытталғанын көрсетеді.

2.5-сурет Енді денені
Бұл формуладан байқайтынымыз, тартылыс өрісінде істелінген жұмыс орын ауыстыру траекториясына байланыссыз, ол тек қана дененің бастапқы және соңғы орнымен анықталады, яғни тартылыс күші консервативті, ал тартылыс өрісі потенциалды болады. Бізге консервативті күштер әсерінен істелген жұмыс жүйенің “-“ теріс таңбалы потенциалдық энергиясының өзгерісі екені белгілі:
Соңғы (2.18) формуласын пайдалана отырып, былай жазамыз:
Мұнда екі күйдегі потенциалдық энергияның айырымы есепке алынған, біз есепті оңайлату үшін Бірлік массалы денені тартылыс өрісінде шексіздіктен белгілі бір нүктеге орын ауыстырған кездегі істелген жұмыстың шамасымен анықталатын, скаляр шаманы тартылыс өрісінің потенциалы деп атаймыз. Сондықтан
Мұндағы
Енді тартылыс өрісідегі
мұндағы Ал “-“ таңбасы кернеулік векторының
Мысал ретінде Жерден Сонымен бізге бұрыннан белгілі потенциалдық энергияның формуласын қорытып шығардық. Космостық жылдамдықтар.Ракетаны космос кеңістігіне ұшыру үшін, біз әуелі ракетаға бастапқы космостық жылдамдықтар деп аталатын жылдамдықтар беруіміз керек. Бұл жылдамдықтарды бүкіл әлемдік тартылыс заңында қарастырамыз. Бірінші космостық немесе радиусы
Есептейтін болсақ Енді екінші космостық жылдамдықты анықтайық. Осы жылдамдықтың арқасында, спутник жердің тарту күші әсерінен шығып кетіп, күннің серігіне айналады. Бұл кезде дене
Осыдан Бақылау сұрақтары: 1. Қандай санақ жүйесін инерциялды дейміз? 2. Күш деген не, оны қалай сипаттауға болады? 3. Ньютонның үш заңы қалай тұжырымдалады? 4. Механикалық жүйе дегеніміз не? 5. Инерциалды емес жүйенің инерциалды санақ жүйесінен айырмашылығы? Әдебиеттер: НӘ1,4,6; ҚӘ2,5; ӘН1 №3 дәріс Сақталу заңдары Механикалық жүйенің масса центрі және оның қозғалыс заңы. Импульстың сақталу заңы.Энергия қозғалыстар мен өзара әрекеттесудің әр түрлерінің әмбебап өлшемі екендігі. Күш жұмысы және оны қисық сызықты интеграл арқылы өрнектеу. Қуат. Механикалық жүйенің кинетикалық энергиясы және оның жүйеге түсірілген сыртқы және ішкі күштердің жұмысымен байланысы. Сыртқы күш өрісіндегі материялық нүктенің потенциалдық энергиясы және оның материялық нүктеге әсер ететін күшпен байланысы. Консервативті, консервативті емес күштер. Күш өрісіндегі қозғалыс. Энергияның сақталу заңы. Кеңістік пен уақыт симметриясының салдары. Механикалық жүйенің масса центрі және оның қозғалыс заңы. Классикалық механикада масса жылдамдыққа тәуелсіз болғандықтан, жүйенің қозғалыс мөлшерін оның массалар орталығының (центрі) жылдамдығы арқылы жазуға болады. Массалар орталығы деп орны осы жүйенің массасының таралуын сипаттайтын елестету С нүктесін айтамыз. Оның радиус-векторы мынаған тең:
мұндағы
мұндағы
деп жазуға болады, яғни жүйенің қозғалыс мөлшері жүйенің массасы мен массалар орталығының жылдамдығының көбейтіндісіне тең. Соңғы өрнекті түрлендірсек, онда:
Сонымен жүйенің массалар орталығы жүйенің барлық массасы осы нүктеге жинақталған және әсер етуші күш, осы жүйеге әсер ететін сыртқы күштердің геометриялық қосындысына тең материалдық нүкте сияқты қозғалады. (3.4) өрнек массалар орталығының қозғалыс заңы болып табылады. (3.3) өрнегіне сәйкес импульстің сақталу заңынан, тұйық жүйенің массалар орталығы түзу сызықты және бірқалыпты қозғалысын немесе тыныштық күйін сақтайды. Қозғалыс мөлшерінің (импульстің) сақталу заңы. Қозғалыс мөлшерінің сақталу заңын қорытып шығару үшін кейбір түсініктерді енгізейік. Материалдық нүктелердің немесе денелердің жиынын бүтін бір жүйе ретінде қарастырамыз. Оны механикалық жүйе деп атаймыз. Механикалық жүйедегі материалдық нүктелер арасындағы әсерлесу күштерін ішкі әсерлесу күштері деп атайды. Ал, сыртқы күштер деп, берілген жүйеге кірмейтін материалдық нүктелермен әсерлесу нәтижесінде пайда болатын күштерді атайды. Денелердің механикалық жүйесіне сыртан ешқандай күш әсер етпесе, онда ол жүйені тұйық жүйе деп атайды. Кез-келген
Ньютонның үшінші заңы бойынша механикалық жүйенің ішкі күштерінің геометриялық қосындысының нөлге тең екенін ескерсек
Поиск по сайту: |
 (2.11)
(2.11) -дененің қатаңдық коэффициенті,
-дененің қатаңдық коэффициенті, 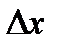 – орын ауыстыру.
– орын ауыстыру. нүктесіне бекітілген серіппені қарастырайық. Серіппеге
нүктесіне бекітілген серіппені қарастырайық. Серіппеге 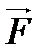 күшімен әсер етіп, оны
күшімен әсер етіп, оны  ұзартайық. Әруақытта серпімді күш деформацияны туғызатын күшке шамасы жағынан тең, ал бағыты жағынан қарама-қарсы болады:
ұзартайық. Әруақытта серпімді күш деформацияны туғызатын күшке шамасы жағынан тең, ал бағыты жағынан қарама-қарсы болады: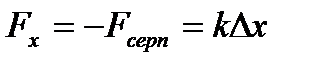 .
.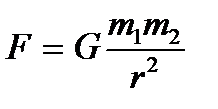 (2.12)
(2.12)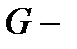 гравитациялық тұрақты деп аталады. Оның физикалық мағынасы мен мәнін алғаш рет тәжрибе жүргізген ағылшын физигі Г.Кавендиш (1731-1810ж).
гравитациялық тұрақты деп аталады. Оның физикалық мағынасы мен мәнін алғаш рет тәжрибе жүргізген ағылшын физигі Г.Кавендиш (1731-1810ж). , бір-бірінен қашықтығы
, бір-бірінен қашықтығы  болатын екі дене бір-біріне шамамен
болатын екі дене бір-біріне шамамен  күшпен тартылады, яғни
күшпен тартылады, яғни  . Бұл өте кішкентай шама, егер денелердің массалары үлкен болса, олардың арасындағы әсерлесу күші өте әлсіз болады. Сондықтан әсерлесуші өлшемі үлкен денелерді 2.2-суреттегідей, элементар бөлшектерге (материалдық нүктелерге) бөліп, солардың арасындағы әсерлесуші күштердің геометриялық қосындысын аламыз:
. Бұл өте кішкентай шама, егер денелердің массалары үлкен болса, олардың арасындағы әсерлесу күші өте әлсіз болады. Сондықтан әсерлесуші өлшемі үлкен денелерді 2.2-суреттегідей, элементар бөлшектерге (материалдық нүктелерге) бөліп, солардың арасындағы әсерлесуші күштердің геометриялық қосындысын аламыз:
 ,
, 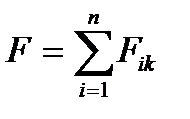
 қозғалысқа келеді. Сонықтан жермен байланысты санақ системасындағы массасы
қозғалысқа келеді. Сонықтан жермен байланысты санақ системасындағы массасы  кез-келген денеге ауырлық күші
кез-келген денеге ауырлық күші  деп аталатын күштің әсер ететіндігі көрсетеді:
деп аталатын күштің әсер ететіндігі көрсетеді: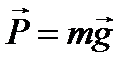 (2.13)
(2.13) тең деп аламыз.
тең деп аламыз.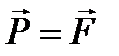 немесе
немесе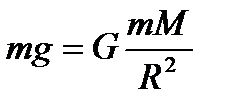 (2.14)
(2.14)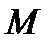 – жердің массасы,
– жердің массасы, 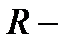 жердің радиусы. Бұл формула дене тек жердің бетінде тұрған жағдайға арналған, ал жерден
жердің радиусы. Бұл формула дене тек жердің бетінде тұрған жағдайға арналған, ал жерден  биіктікте орналасса:
биіктікте орналасса: (2.14)
(2.14) деген ұғым бар. Дененің Жерге тартылуы салдарынан тіреуіш не ілмекке түсетін күшін дененің салмағы деп атайды. Ілмек не тіреуіш дененің еркін құлауынан ұстап тұрады. Салмақ қарастырылып отырған денеге түсірілмейді, ол ілмекке әсер етеді. Дененің салмағы мынандай жағдайда көрінеді: егер дене ауырлық өрісінде үдемелі
деген ұғым бар. Дененің Жерге тартылуы салдарынан тіреуіш не ілмекке түсетін күшін дененің салмағы деп атайды. Ілмек не тіреуіш дененің еркін құлауынан ұстап тұрады. Салмақ қарастырылып отырған денеге түсірілмейді, ол ілмекке әсер етеді. Дененің салмағы мынандай жағдайда көрінеді: егер дене ауырлық өрісінде үдемелі  қозғалса, онда оған ауырлық күшінен басқа қосымша күш
қозғалса, онда оған ауырлық күшінен басқа қосымша күш 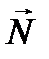 әсер етеді. Ньютонның екінші заңы бойынша:
әсер етеді. Ньютонның екінші заңы бойынша: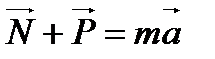 (2.15)
(2.15) тең. Бұл кезде дене тыныштықта немесе бірқалыпты түзусызықты қозғалыста болады, яғни
тең. Бұл кезде дене тыныштықта немесе бірқалыпты түзусызықты қозғалыста болады, яғни  . Ал егер дене ауырлық өрісінде еркін кезөкелген траектория бойымен және кезөкелген бағытта қозғалса, яғни
. Ал егер дене ауырлық өрісінде еркін кезөкелген траектория бойымен және кезөкелген бағытта қозғалса, яғни 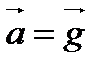 болса, онда
болса, онда  , яғни дене салмақсыздықта болады. Мысалы: космос әлемінде еркін қозғалатын космостық корабльдердегі дене салмақсыздық күйде болады.
, яғни дене салмақсыздықта болады. Мысалы: космос әлемінде еркін қозғалатын космостық корабльдердегі дене салмақсыздық күйде болады. бұл формуладан
бұл формуладан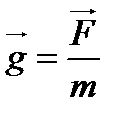 (2.16)
(2.16) векторы
векторы 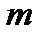 массаға байланыссыз, тартылыс өрісінің кернеулігі деп аталады. Тартылыс өрісінің кернеулік векторы өріс жағынан әсер етуші
массаға байланыссыз, тартылыс өрісінің кернеулігі деп аталады. Тартылыс өрісінің кернеулік векторы өріс жағынан әсер етуші  күші арқылы анықталады: бірлік массалы материалдық нүктеге өріс жағынан әсер етуші күш, кернеулік деп аталады.
күші арқылы анықталады: бірлік массалы материалдық нүктеге өріс жағынан әсер етуші күш, кернеулік деп аталады. 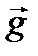 бағыты
бағыты 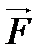 күшінің бағытымен бағыттас. Кереулік күш сызықтары арқылы сипатталады. Күш сызықтарының кез-келген нүктесіне тұрғызылған жанама (2.3-сурет) кернеулік векторын береді.
күшінің бағытымен бағыттас. Кереулік күш сызықтары арқылы сипатталады. Күш сызықтарының кез-келген нүктесіне тұрғызылған жанама (2.3-сурет) кернеулік векторын береді.
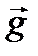

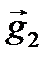 A
A 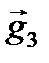

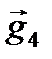
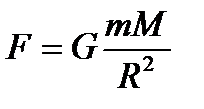
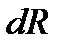 -ге орын ауыстырғандағы істелінген жұмысы:
-ге орын ауыстырғандағы істелінген жұмысы: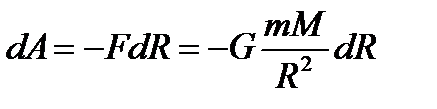 (2.17)
(2.17) қашықтықтан
қашықтықтан 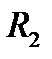 қашықтыққа орын ауыстырғанда жасалатын жұмысы:
қашықтыққа орын ауыстырғанда жасалатын жұмысы: яғни
яғни  (2.18)
(2.18) .
.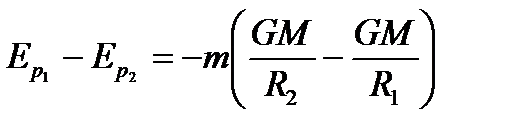 (2.19)
(2.19) ұмтылдырып шек аламыз:
ұмтылдырып шек аламыз: 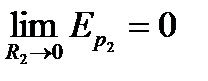 . Сонда
. Сонда 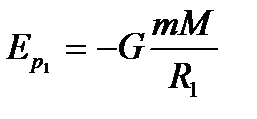 бірінші нүкте еркімізше алынған нүкте болғандықтан, былай жазуға болады.
бірінші нүкте еркімізше алынған нүкте болғандықтан, былай жазуға болады. 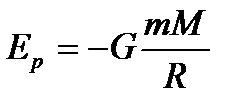 бұл формула тартылыс өрісіндегі потенциалық энергия деп аталады. Бұдан
бұл формула тартылыс өрісіндегі потенциалық энергия деп аталады. Бұдан 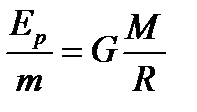 қатынас алуға болады. Потенциалық энергияның
қатынас алуға болады. Потенциалық энергияның 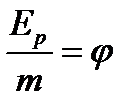 - тартылыс өрісін энергиялық сипаттамасын потенциал деген шаманы береді.
- тартылыс өрісін энергиялық сипаттамасын потенциал деген шаманы береді. немесе
немесе 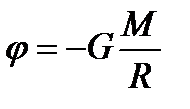 (2.20)
(2.20) -дене мен қарастырып отырған нүктенің ара қашықтығы.
-дене мен қарастырып отырған нүктенің ара қашықтығы. потенциалдары бірдей барлық геометриялық нүктелер,
потенциалдары бірдей барлық геометриялық нүктелер,  сфералық бет тудырады. Ондай беттерді, яғни барлық нүктелердегі потенциалдары бірдей болатын беттерді эквипотенциалдық беттер деп атайды.
сфералық бет тудырады. Ондай беттерді, яғни барлық нүктелердегі потенциалдары бірдей болатын беттерді эквипотенциалдық беттер деп атайды. 
 (потенциал) мен
(потенциал) мен  , ал
, ал 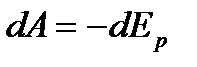 . Күш өрісінің әсерінен массасы
. Күш өрісінің әсерінен массасы  элементар жұмысы мынаған тең:
элементар жұмысы мынаған тең:  , ал екінші жағынан
, ал екінші жағынан 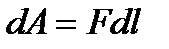 ,
,  ауырлық күшінің әсерінен дененің
ауырлық күшінің әсерінен дененің 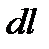 - элементар орын ауыстыруынан
- элементар орын ауыстыруынан 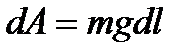 . бұдан:
. бұдан: 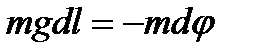 немесе
немесе 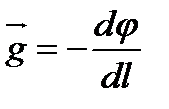 ;
; 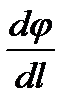 - мәні тартылыс өрісінде орын ауыстыру бағытындағы бірлік ұзындықта потенциалдық өзгеруін сипаттайды. Оны былай да жазуға болады:
- мәні тартылыс өрісінде орын ауыстыру бағытындағы бірлік ұзындықта потенциалдық өзгеруін сипаттайды. Оны былай да жазуға болады: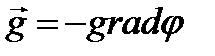 (2.21)
(2.21) скаляр
скаляр  -дің градиенті.
-дің градиенті. мұндағы
мұндағы 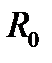 - Жердің радиусы. Бізге
- Жердің радиусы. Бізге 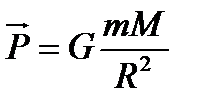 және
және 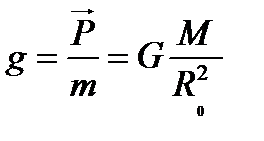 белгілі,
белгілі,  ескере отырып, мынаны аламыз:
ескере отырып, мынаны аламыз: 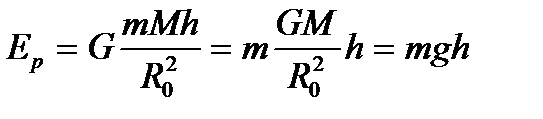 .
.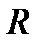 жер радиусымен шамалас дөңгелек орбита бойымен жерді айнала қозғалу үшін, денеге белгілі бір
жер радиусымен шамалас дөңгелек орбита бойымен жерді айнала қозғалу үшін, денеге белгілі бір  жылдамдық береміз. Бұл кезде дене жердің жасанды серігіндей қозғалыста болады. Радиусы
жылдамдық береміз. Бұл кезде дене жердің жасанды серігіндей қозғалыста болады. Радиусы 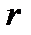 орбита боймен қозғалған денеге Жердің ауырлық күші әсер етіп, оған
орбита боймен қозғалған денеге Жердің ауырлық күші әсер етіп, оған 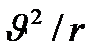 центрге тартқыш үдеу береді:
центрге тартқыш үдеу береді:  бұдан
бұдан 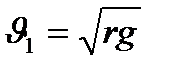 немесе Ньютонның екінші заңы бойынша центрге тартқыш күш пен бүкіл әлемдік тартылыс күшін теңестіріп
немесе Ньютонның екінші заңы бойынша центрге тартқыш күш пен бүкіл әлемдік тартылыс күшін теңестіріп  ,
,  бұдан
бұдан  . Екі жағын да
. Екі жағын да  , яғни
, яғни 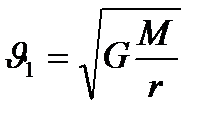 , мұндағы
, мұндағы 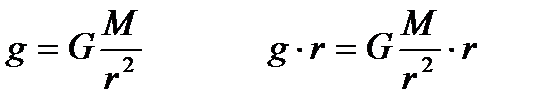 . Жердің жасанды серігін Жердің бетінен алыс емес десек, онда
. Жердің жасанды серігін Жердің бетінен алыс емес десек, онда  (жердің радиусы). Сонда бірінші космостық жылдамдық:
(жердің радиусы). Сонда бірінші космостық жылдамдық: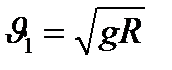 (2.22)
(2.22) жердің жасанды серігі болуы үшін оған бірінші космостық жылдамдық береді,
жердің жасанды серігі болуы үшін оған бірінші космостық жылдамдық береді,  ие болған дене Жерге құлап түспейді, бірақ Жердің тартылу сферасынан шығып кетпейді. (Жерді айнала дөңгелек орбита бойымен қозғалады)
ие болған дене Жерге құлап түспейді, бірақ Жердің тартылу сферасынан шығып кетпейді. (Жерді айнала дөңгелек орбита бойымен қозғалады) жұмысын істеуге жетерліктей энергия қорына ие болуы керек:
жұмысын істеуге жетерліктей энергия қорына ие болуы керек: немесе
немесе  .
.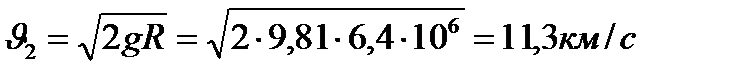 . Бұл
. Бұл  ден
ден 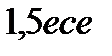 көп жылдамдық, күнді айнала парабола бойымен қозғалады. Ал үшінші космостық жылдамдық
көп жылдамдық, күнді айнала парабола бойымен қозғалады. Ал үшінші космостық жылдамдық  планеталар арасында гипербола бойымен қозғалатын жылдамдық.
планеталар арасында гипербола бойымен қозғалатын жылдамдық. (3.1)
(3.1)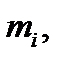
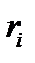 –
–  - ші материалдық нүктенің массасы мен радиус-векторы,
- ші материалдық нүктенің массасы мен радиус-векторы, 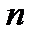 – жүйенің материалдық нүктелер саны,
– жүйенің материалдық нүктелер саны,  - жүйенің массасы. Массалар орталығының жылдамдығы:
- жүйенің массасы. Массалар орталығының жылдамдығы: (3.2)
(3.2) , ал
, ал 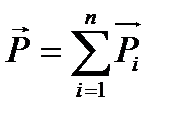 жүйенің импульсі десек, онда
жүйенің импульсі десек, онда (3.3)
(3.3) (3.4)
(3.4) денелерден тұратын механикалық жүйені қарастырамыз. Олардың массалары
денелерден тұратын механикалық жүйені қарастырамыз. Олардың массалары 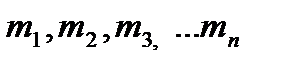 және жылдамдықтары
және жылдамдықтары  болсын. Егер
болсын. Егер  әсер етуші ішкі күштер жиынтығы деп, ал
әсер етуші ішкі күштер жиынтығы деп, ал  әсер етуші сыртқы күштер жиынтығы деп алсақ, онда кез-келген дене үшін Ньютонның екінші заңын былай жазуға болады:
әсер етуші сыртқы күштер жиынтығы деп алсақ, онда кез-келген дене үшін Ньютонның екінші заңын былай жазуға болады: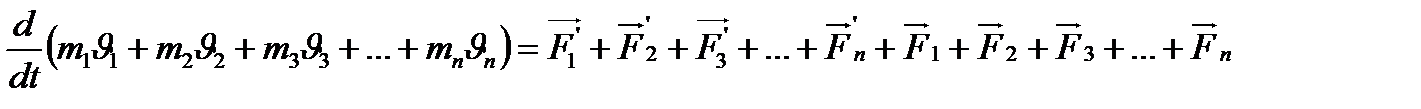
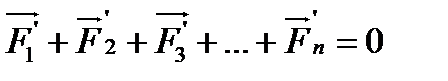 .
.