 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 8 страница

7.2-сурет
Эйнштейннің ІІ постулаты бойынша, екі жүйедегі жарық жылдамдығы бірдей және с-ға тең. Сондықтан егер
арақашықтық жүрсе, онда К
мұндағы Эйнштейн салыстырмалылық теориясында Галилейдің классикалық түрлендірулері, постулаттарды қанағаттандыратын Лоренц түрлендірулеріне ауыстырылатынын көрсетеді. Лоренц түрлендірулерін мына формулалар түрінде жазуға болады:
мұндағы Келтірілген теңдеулер симметриялы және тек Егер Сонымен қатар, кеңістік және уақыт түрлендіруі тәуелсіздік емес, себебі координат түрлендіру заңына уақыт енеді, ал уақыт түрлендіру заңына кеңістік координаттары, яғни кеңістік және уақыт өзара байланыстылығы орнатылады. Эйнштейн теориясы, кеңістіктер-уақыттар координаттар үздіксіз байланысын қарастырып, кеңістік –уақыт төрт өлшемін құрайды. Түрлендірудің инварианттары: Лоренцше түрлендіру формулаларынан маңызды бірнеше қорытындылар шығады. Енді солардың кейбіреулеріне тоқталайық. 1. Оқиғалардың бір мезгілдігі. Мысалы, К жүйесінде координаталары х1 және х2 нүктелерінде t1 және t2 мезеттерде бір-бірден екі оқиға болған болсын. К/ жүйесінде сонда оларға х1 Ал, егер оқиға кеңістікте әр нүктеде х1 ≠ х2 , бірақ бір мезгілде t1= t2 болса, онда (5.8) формулаларға сәйкес К/ жүйеде Лоренц түрлендіруінше
Демек, Сонымен бұл құбылыстар К 2. Түрліше жүйелердегі дене ұзындықтарын салыстыру.Бұрынғыша инерциялық К және К
сонда мұндағы 3.Түрліше жүйелердегі оқиғалар ұзақтылықтарын салыстыру. Жоғарыда айтылғандай екі санақ жүйесінен алайық.Мысалы К
Сонда оқиғаның осы, К жүйесіндегі ұзақтылығы
мұндағы τ уақыт аралығы К жүйесі сағаты (тыныш тұрған сағат), ал t Жылдамдықтарды қосу теоремасы. Бұрын айтылғандай К Бұл дененің К
яғни Осы (5.11) өрнек жылдамдықты қосу теоремасы деп аталады. Егер
Мұнда қосылушы Материалдық нүктенің релятивистік динамикасының негізгі заңы. Қозғалыстағы релятивистік бөлшектердің массасы олардың жылдамдықтарына тәуелді.
Сонымен, әр түрлі инерциалдық санақ жүйесінде бір бөлшектің массасы әр түрлі. Бір инерциалдық санақ жүйесінен екіншіге ауысқанда табиғаттың барлық заңдары инвариантты екенін бекітетін Эйнштейннің салыстырмалылық принципінен Лоренц түрлендірулеріне қарасты физикалық заңдардың теңдеулерін инвариантты шарты шығады: Динамиканың негізгі Ньютон заңы Лоренцтің түрленуіне қатысты инвариантты болады, егер оның оң жағында релятивистік импульстің уақыт бойынша туындысы тұрса. Материалдық нүктенің релятивистік динамикасының негізгі заңының түрі мынадай болады
мұндағы материалдық нүктенің релятивистік импульсі. Кеңістіктің біртектілігіне байланысты релятивистік механикада релятивистік импульстің сақталу заңы орындалады: тұйық жүйенің релятивистік импульсі сақталады, яғни уақыт өтуіне байланысты өзгермейді. Масса және энергияның өзара байланыс заңы.Релятивистік бөлшектің кинетикалық энергиясын табамыз. Өткен классикалық механикада белгілі элементар орын ауыстырғандағы материалдық нүктенің кинетикалық энергиясының өсімшесі, осы орын ауыстырғандағы күш жұмысына тең
мұндағы
яғни бөлшектің кинетикалық энергиясының өсімшесі оның массасының өсімшесіне пропорционал. Тыныштықта бөлшектің кинетикалық энергиясы нольге тең, ал оның массасы тыныштықтағы массасына тең, ендеше (5.16) теңдеуді интегралдап, аламыз
осы теңдеу, егер Осыдан А.Эйнштейн дененің толық энергиясы мен оның массасының арасындағы байланыстың универсиалды екенін көрсетеді:
(5.17) және (5.18) теңдеулер табиғаттың фундаментальды заңын көрсетеді - масса мен энергияның арасындағы өзара байланыс заңы: жүйенің толық энергиясы оның массасы мен вакуумдағы жарық жылдамдығының квадрат көбейтіндісіне тең. Толық энергияға сыртқы күш өрісіндегі дененің потенциалдық энергиясы кірмейді. (5.18) заңды, (5.17) ескере отырып, былай да жазуға болады:
осыдан , тыныштықтағы дененің энергиясы ( Бақылау сұрақтары: 1. Салыстырмалықтың механикалық принципінің физикалық мағынасы неде? 2. Арнайы салыстырмалық теория постулаттарының негізі неде? 3. Дененің жылдамдығы санақ жүйесінің қозғалу жылдамдығына тәуелді ме? 4. Лоренц түрлендіруін жазыңдар және түсіндіріңдер. Қандай жағдайда олар Галилей түрлендіруіне ауысады? 5. Лоренц түрлендіру негізінен кеңістік және уақыт жөнінде қандай қорытынды жасауға болады? 6. Әртүрлі санақ жүйесінде дененің өлшемдері және уақиғаның ұзақтығы үшін арнайы салыстырмалы теориядан қандай салдарлар шығады? 7. Релятивистік динамика заңының негізгі түрі қандай? Ол Ньютон механика заңы негізінен айырмашылығы неде? Релятивистік импульс сақталу заңы. Әдебиеттер: НӘ1,4,6; ҚӘ2,5; ӘН1 №6 дәріс Тұтас орта механикасының элементтері Тұтас орта ұғымы. Сұйықтар мен газдардың жалпы қасиеттері. Идеал және тұтқыр сұйық. Бернулли теңдеуі. Сұйықтардың ламинарлық және турбуленттік ағысы. Тұтқырлық. Стокс, Пуазейль формулалары. Тұтас орта ұғымы. Сұйықтар мен газдардың жалпы қасиеттері. Сұйықтағы және газдағы қысым. Сұйықтар мен газдардың қозғалысын және тепе-теңдік заңдарын, сол сияқты олардың қатты денелермен әсерлесуін зерттейтін физиканың тарауын гидромеханика деп атайды. Гидромеханикада сұйықтың не газдың нақты құрылысы ескерілмейді, олар кеңістікте үзіліссіз таралған тұтас орталар ретінде қарастырылады. Тұтас орта моделі аса сиретілген газдар үшін қолдануға жарамсыз. Сұйықтар мен газдардың қатты денелерден айырмашылығы – олар өз пішіндерін сақтамайды, құйылған ыдыстың пішінін қабылдайды. Сұйықтар газдардан оларда беттік қабаттың болмайтындығымен, бірдей жағдайларда тығыздығының үлкендігімен (кризистік күйден басқа жағдайда), тығыздықтың қысымға тәуелділік сипатымен және сұйықтардың іс жүзінде сығылмайтындығымен ерекшеленеді. Кез келген тыныштықтағы сұйыққа жұқа пластина салатын болсақ, онда пластинаның
Қысымның өлшем бірлігі – Паскаль: 6.1-суретте
6.1-сурет Тепе-теңдік сұйықтардағы қысым Паскаль заңына бағынады: сұйықтың берілген нүктесіндегі қысым барлық бағыттарда бірдей, сұйықтың алып отырған барлық көлемі бойынша бірдей қысым береді. Сұйықтың салмағы осы сығылмайтын тыныштықтағы сұйықтың ішіндегі қысымның таралуына қалай әсер ететінін қарастырайық. Егер сұйық сығылмайтын болса, онда оның тығыздығы қысымға тәуелсіз. Онда көлденең аққан сұйықтың ағысы
яғни қысым биіктік бойынша сызықты өзгереді. Сұйықтың қалыптасқан қозғалысы. Сығылғыштығы және тұқырлығы ескерілмейтін тұтас ортадағы идеал сұйықтың қозғалысын қарастырайық. Сұйық қозғалысын қарастырғанда көп жағдайда сұйықты мүлдем сығылмайды деп санауға және оның бір қабаты екінші қабатымен салыстырмалы қозғалса, үйкеліс күштері (тұтқырлық) пайда болмайды деп қарауға болады. Мұндай сұйықты идеал сұйық деп атайды. Сұйық қозғалысын жете түсіну үшін ағын сызықтары және ағын түтігі деген түсініктерді пайдаланамыз. Қозғалыстағы сұйық үшін, оның әрбір нүктесіне жүргізілген жанама
Поиск по сайту: |











 уақытта К жүйесінде сигнал А нүктесіне дейін жеткенше,
уақытта К жүйесінде сигнал А нүктесіне дейін жеткенше, (5.6)
(5.6) жүйесінде жарық импульсі А нүктесіне жеткен мезетінде
жүйесінде жарық импульсі А нүктесіне жеткен мезетінде (5.7)
(5.7) -жарық импульсінің К
-жарық импульсінің К 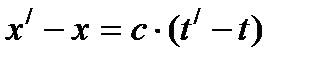 . К жүйесіне қатысты К
. К жүйесіне қатысты К 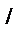 жүйесі орын ауыстырады. Сондықтан
жүйесі орын ауыстырады. Сондықтан  , онда
, онда  , Яғни К және К
, Яғни К және К 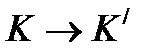



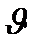 -ның алдындағы таңбамен ғана ажыратылады. Лоренц түрлендірулерін талдай келіп, мынадай қорытындылар жасауға болады:
-ның алдындағы таңбамен ғана ажыратылады. Лоренц түрлендірулерін талдай келіп, мынадай қорытындылар жасауға болады: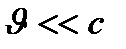 болса, яғни
болса, яғни  , онда Лоренцше түрлендірулер Галилейше түрлендіру формуласына айналады. Сөйтіп салыстырмалы жылдамдық жарықтың вакуумдағы жылдамдығынан кем болса ғана Галилейше түрлендіруде мағына бар. Егер
, онда Лоренцше түрлендірулер Галилейше түрлендіру формуласына айналады. Сөйтіп салыстырмалы жылдамдық жарықтың вакуумдағы жылдамдығынан кем болса ғана Галилейше түрлендіруде мағына бар. Егер  >c болса, онда жоғардағы формулалар бойынша x
>c болса, онда жоғардағы формулалар бойынша x 
 ,
, 
 . К
. К  болады, мұндағы х1
болады, мұндағы х1  координаталары. Уақыт өзгермеген жағдайда Лоренцше түрлендірудің (7.8) формулалары бойынша:
координаталары. Уақыт өзгермеген жағдайда Лоренцше түрлендірудің (7.8) формулалары бойынша:
 немесе
немесе  (5.9)
(5.9) =t2
=t2 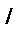
 мен t2
мен t2 
 немесе
немесе  (5.10)
(5.10) және
және 
 , К жүйеге қатысты жылдамдығы
, К жүйеге қатысты жылдамдығы 
 , бұдан
, бұдан 
 немесе
немесе  (5.11)
(5.11) пен
пен  әрқайсысы жарық жылдамдығынан әлде қайда аз болса,онда өрнек жылдамдықтары классикалық, механикаша қосу, өрнегіне айналады:
әрқайсысы жарық жылдамдығынан әлде қайда аз болса,онда өрнек жылдамдықтары классикалық, механикаша қосу, өрнегіне айналады: ,
, 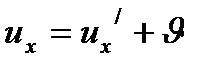
 жылдамдықтар жарықтың с жылдамдықтан кем болады. Егер
жылдамдықтар жарықтың с жылдамдықтан кем болады. Егер  =c болса, онда
=c болса, онда  =c, яғни салыстырмалық теорияның екінші постулатына сай жарықтың с вакуумдағы жылдамдығы санақ жүйесінің қозғалыс жылдамдығына тәуелді емес.
=c, яғни салыстырмалық теорияның екінші постулатына сай жарықтың с вакуумдағы жылдамдығы санақ жүйесінің қозғалыс жылдамдығына тәуелді емес.  (5.12)
(5.12) .
. немесе
немесе  (5.13)
(5.13) (5.14)
(5.14) немесе
немесе 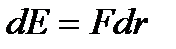 (5.15)
(5.15) ескере отырып және (5.13) –шы теңдеуді (5.15) –ке қойып, мына теңдеуді аламыз:
ескере отырып және (5.13) –шы теңдеуді (5.15) –ке қойып, мына теңдеуді аламыз:
 екенін ескере отырып, осы теңдеуді және (5.12) формуланы түрлендіріпмынадай қорытындыға келеміз:
екенін ескере отырып, осы теңдеуді және (5.12) формуланы түрлендіріпмынадай қорытындыға келеміз: (5.16)
(5.16) немесе
немесе  (5.17)
(5.17) классикалыққа айналады
классикалыққа айналады  . Эйнштейннің (5.16) теңдеуін қорыта келіп, бұл тек кинетикалық энергия үшін әділетті емес, сонымен қатар толық энергияға да қатысты. Кез келген массаның өзгеруі
. Эйнштейннің (5.16) теңдеуін қорыта келіп, бұл тек кинетикалық энергия үшін әділетті емес, сонымен қатар толық энергияға да қатысты. Кез келген массаның өзгеруі  материалдық нүктенің толық энергиясының өзгеруімен сипатталады:
материалдық нүктенің толық энергиясының өзгеруімен сипатталады: 
 (5.18)
(5.18)
 )
)  болады.
болады. ауданына жан-жағында тұрған сұйықтың бөлігі
ауданына жан-жағында тұрған сұйықтың бөлігі  күшпен әсер етеді. Әсер күші модулы жағынан бірдей, әрі пластинаның қалай тұрғанына байланыссыз, ол бағыты жағынан
күшпен әсер етеді. Әсер күші модулы жағынан бірдей, әрі пластинаның қалай тұрғанына байланыссыз, ол бағыты жағынан 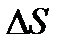 ауданға перпендикуляр әсер етеді де пластинаны қозғалысқа келтіреді. Сұйықтың жағынан бірлік ауданға нормаль күштің әсерінен анықталатын физикалық шама қысым деп аталады:
ауданға перпендикуляр әсер етеді де пластинаны қозғалысқа келтіреді. Сұйықтың жағынан бірлік ауданға нормаль күштің әсерінен анықталатын физикалық шама қысым деп аталады: (6.1)
(6.1) беттің ауданына бірқалыпты нормаль түсірілген
беттің ауданына бірқалыпты нормаль түсірілген  күшнің тудыратын қысымы
күшнің тудыратын қысымы 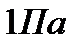 -ға тең.
-ға тең.
 , оның биіктігі
, оның биіктігі  және тығыздығы
және тығыздығы  десек, салмағы
десек, салмағы  , ал төменгі қабатындағы қысымы
, ал төменгі қабатындағы қысымы (6.2)
(6.2) гидростатикалық қысым деп аталады. Бұл теңдеу бойынша сұйықтар немесе газдардағы қысымның тереңдікке тәуелділігі оларға батырылған кез-келген денеге әсер ететін кері итеруші күштің пайда болуын тудырады.
гидростатикалық қысым деп аталады. Бұл теңдеу бойынша сұйықтар немесе газдардағы қысымның тереңдікке тәуелділігі оларға батырылған кез-келген денеге әсер ететін кері итеруші күштің пайда болуын тудырады. векторының бағытына дәл келетіндей етіп сызықтар жүргіземіз. Бұл сызықтар ағын сызықтары деп аталады (6.2-сурет). Ағын сызықтармен шектелген сұйық бөлігі ағын түтігі деп аталады. Егер жылдамдық векторы кеңістіктің әрбір нүктесінде тұрақты болса, онда ағын орныққан немесе стационар ағын деп аталады.
векторының бағытына дәл келетіндей етіп сызықтар жүргіземіз. Бұл сызықтар ағын сызықтары деп аталады (6.2-сурет). Ағын сызықтармен шектелген сұйық бөлігі ағын түтігі деп аталады. Егер жылдамдық векторы кеңістіктің әрбір нүктесінде тұрақты болса, онда ағын орныққан немесе стационар ағын деп аталады.