 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 9 страница
6.2 -сурет Әдетте сұйықтың ағысы күшті болғанда ағын сызықтары жиі, ал сұйық ағысы бәсең жерде ағын сызықтары сирек жүргізіледі. Ағын түтігінің белгілі бір қимасында барлық бөлшек қозғалыс кезінде ағын түтігінен шығып кетпей, оның ішімен қозғалады. Сонымен қатар, ағын түтігінің ішіне де сырттан ешқандай бөлшектер енбейді. Ағын түтігі бойымен үзіліссіз сұйық ағып жатсын 6.3-суреттегідей. Ағын түтігі бойынан бөлшек жылдамдығының бағытына перпендикуляр
6.3 -сурет Сұйықтың қалыптасқан ағыны кезінде сұйық сығылмайды деп есептесек, онда
Осы өрнекті ағынның үздіксіздік теңдеуі деп атайды. Ағын түтігі көлденең қимасының сұйық ағысының жылдамдығына көбейтіндісі тұрақты шама болады. Түтік бойындағы сұйық ағынының жылдамдығы түтіктің көлденең қималарының ауданына кері пропорционал, яғни түтік қимасы жіңішке болса, ағын жылдамдығы үлкен, керісінше қима үлкен болса, жылдамдық аз. Сондықтан, түтіктің тарлау жеріне ағып барған сұйыққа сол түтіктің кең жеріндегі сұйық тарапынан күш әсер етеді. Бұл күш сұйықтың әртүрлі бөліктеріндегі қысымдар айырымының есебінен пайда болады. Күш түтіктің жіңішке жағына қарай бағытталғандықтан түтіктің жуан жеріндегі қысым оның жіңішке жеріндегі қысымнан артық болады. Идеал және тұтқыр сұйық. Бернулли теңдеуі. Идеал сұйықтың қозғалысын (ағысын) сипаттайтын өрнекті 1738 жылы Д. Бернулли тұжырымдады. Бұл формуланы қорытып шығару үшін көлденең қималар әртүрлі түтікшедегі идеал сұйықтың қозғалысын қарастырайық (6.4-сурет). Түтікшенің ішінен Түтік белгілі-бір еңістікке ие және олардың
Бұл өзгеріс, энергияның сақталу заңы бойынша сыртқы күштердің жұмысына негізделген. Берілген жағдайда сәйкес
6.4-сурет Энергияның сақталу заңы бойынша қималар энергияларының айырымы сұйықты қозғалысқа келтіру үшін істелінетін жұмыстардың айырымына тең болады. Сыртқы күштердің қосынды жұмысы
Кинетикалық энергияның өзгерісі жасалынған жұмысқа тең
мұндағы
Бернулли теңдеуі деп аталады. Сұйық ағынындағы қысым. Бернулли теңдеуіндегі:
6.5-сурет Ағын түтігінің горизонтал орналасқан жағдайында (
мұндағы
мұндағы
(6.11) -мен (6.12) өрнектерінен ағын жылдамдығы
Сұйықтың тесіктен ағуы. Сұйық толтырылған ыдыстың түбіне жақын орналасқан ашық тесіктің ауданы
Бернулли теңдеуінен
теңдігін аламыз. Егер Олай болса, сұйықтың ағыс жылдамдығы
мұндағы
6.6-сурет Сондықтан, ыдыс бұл импульсті ағатын Бұл кезде Ньютонның үшінші заңы бойынша ыдысқа
мұндағы Сұйықтардың ламинарлық және турбуленттік ағысы.Тұтқырлық. Сұйықтың ағысын ламинарлық және турбуленттік деп екіге бөледі. Сұйықтың жеке қабаттары бір-бірімен қарағанда параллель, яғни сұйық қабатта бір-бірімен араласпай қозғалатын болса, онда ағысты ламинарлық ағыс деп атайды. Сұйық бөлшектерінің жылдамдығы артып, шекті мәнге жеткенде әр қабаттардың бір-бірімен араласуы сұйықтың турбуленттік ағысы деп атайды. Идеал сұйықтың қалыптасқан стационарлы ағысы кез-келген жылдамдықтарда ламинарлы болып табылады. Нақты сұйықтарда қабаттар арасында ішкі үйкеліс күші пайда болады, яғни нақты сұйықтар тұтқырлыққа ие болады. Сондықтан, әрбір қабат 6.7- суретте көрші қабаттың қозғалысына кедергі жасайды.
6.7-сурет Ішкі үйкеліс күшінің шамасы қабаттарының беттесу
мұндағы Стокс, Пуазейль формулалары. Егер ішкі үйкеліс күші және ағыс жылдамдығы аз шама болса, онда қозғалысты ламинарлық деп қарастыруға болады. Ішкі үйкеліс күшінің үлкен мәндері кезінде ағыстың қабаттық сипаты бұзылады; аса күшті араласу басталады, яғни турбулентті ағысқа көшу болады. Түтік бойымен сұйық ағысы кезіндегі ағыстың бір түрінен екінші түрге өту шарты Рейнольдс саны деп аталатын
мұндағы
мұндағы Тұтқырлықтың әсері ағынның қозғалмайтын денемен өзара әсерлесуі кезінде де байқалады. Тұтқырлығы
Бұл өрнек Стокс теңдеуі деп аталады. (6.21) Стокс өрнегі лабораториялық практикум сабағында сұйықтардың Бақылау сұрақтары: 1. Архимед және Паскаль заңдарын тұжырымдап және түсіндіріңдер. 2. Сығылмайтын сұйықтар үшін үздіксіздік теңдеуінің физикалық мәні қандай және оны қалай өрнектейді? 3. Сұйықтар ағынында статистикалық, динамикалық және толық қысымдарды қалай өлшеуге болады? 4. Бертулли теңдеуін өрнектеңдер 5. Жылдамдық градиенті деген не? 6. Динамикалық тұтқырлық коэфицентінің физикалық мәні қандай? 7. Сұйықтардың қандай ағынын ламинарлық трубуленттік дейді? Рейнольдс саны нені сипаттайды? 8. Стокс және Пуазейль әдістерін практикада пайдалануын түсіндіріңдер. Әдебиеттер: НӘ1,4,6; ҚӘ2,5; ӘН1 №7 дәріс Механикалық тербелістер
Гармониялық тербелістердің жалпы сипаттамасы. Тербелістерді қосу. Векторлық диаграмма. Серіппедегі жүктің тербелісі, математикалық және физикалық маятниктер. Өшу коэффициенті. Өшудің логарифмдік декременті. Синусоидалық күштің әсерінен болатын еріксіз тербелістер. Резонанс.Еріксіз тербелістердің амплитудасы мен фазасы.
Гармониялық тербелістердің жалпы сипаттамасы. Табиғатта өте жиі кездесетін қозғалыстардың қатарына тербелістерді жатқызуға болады. Тербелмелі қозғалыс немесе жай тербеліс деп уақыттың өтуіне байланысты қайталанып отыратын қозғалыстарды айтады. Тербелістің түрі сан алуан болғанымен, олардың барлығы да жалпы заңдылықпен өзгереді. Олардың ең қарапайым түрі гармониялық тербелістер. Синус немесе косинус заңы бойынша уақытқа тәуелді өзгеретін тербелісті гармониялық тербеліс дейді. Ол келесі формуламен өрнектеледі:
мұндағы Уақыт өткен сайын жүйенің қозғалысы дәл қайталанып отырса, онда мұндай тербелісті периодтық деп атайды. Толық бір тербеліске кететін уақыт период (Т) деп аталады. Тербелуші жүйеге үйкеліс күштері әсер етпесе, онда ол еркін тербеледі, оның амплитудасы, периоды өзгермейді. Егер жүйе
Период пен циклдік жиілік арасындағы байланыс
Жиілік Тербелмелі қозғалыс тек
Поиск по сайту: |

 және
және 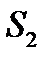 қиманы қарастырайық. Тұрақты қималардағы өтетін сұйық бөлшегінің жылдамдығын
қиманы қарастырайық. Тұрақты қималардағы өтетін сұйық бөлшегінің жылдамдығын  және
және 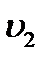 деп белгілейік. Аз уақыт аралығында бұл
деп белгілейік. Аз уақыт аралығында бұл  қималар арқылы өтетін сұйық көлемдері:
қималар арқылы өтетін сұйық көлемдері:
 (6.3)
(6.3)
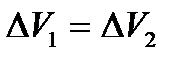 және
және  . Олай болса, ағын түтігінің кез-келген көлденең қимасы үшін келесі қатынас орынды болады:
. Олай болса, ағын түтігінің кез-келген көлденең қимасы үшін келесі қатынас орынды болады: (6.4 )
(6.4 ) ,
, 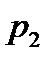 болсын. Сұйықтық
болсын. Сұйықтық 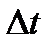 уақыт аралығында
уақыт аралығында  жол жүріп,
жол жүріп,  -ден
-ден  жол жүріп,
жол жүріп,  аралығындағы орналасқан сұйықтың көлміне тең болады.
аралығындағы орналасқан сұйықтың көлміне тең болады.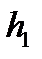 және
және  биіктікте тұр.
биіктікте тұр. және
және  екенін ескеріп, бастапқыда
екенін ескеріп, бастапқыда  (6.5)
(6.5) және
және  , мұндағы
, мұндағы  күш пен
күш пен  орын ауыстырудың бағыттары бірдей, сондықтан
орын ауыстырудың бағыттары бірдей, сондықтан  күш оң жұмыс жасайды және
күш оң жұмыс жасайды және  -ға тең.
-ға тең. қысым күші және
қысым күші және 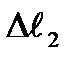 орын ауыстырудың бағыттары қарама-қарсы. Олай болса,
орын ауыстырудың бағыттары қарама-қарсы. Олай болса,  . Сонымен, сыртқы күш
. Сонымен, сыртқы күш  жұмыс жасайды.
жұмыс жасайды.
 - ға тең.
- ға тең. уақыт ішінде
уақыт ішінде  және
және  үздіксіз теоремасы бойынша өзара тең
үздіксіз теоремасы бойынша өзара тең  . Сыртқы күштердің толық жұмысы
. Сыртқы күштердің толық жұмысы (6.6)
(6.6)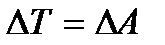 , немесе (6.4) және (6.5) өрнектеріне сәйкес
, немесе (6.4) және (6.5) өрнектеріне сәйкес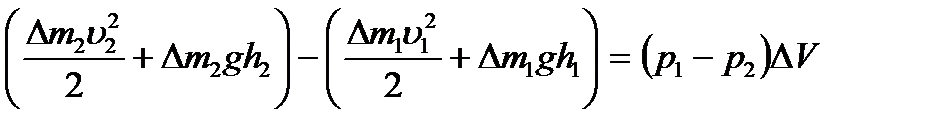 (6.7)
(6.7) теңдігінен және сұйықтың сығылмайтын шартынан
теңдігінен және сұйықтың сығылмайтын шартынан ,
, - сұйық тығыздығы, сондықтан ( 6.6 ) өрнек келесі түрде жазылады:
- сұйық тығыздығы, сондықтан ( 6.6 ) өрнек келесі түрде жазылады: (6.8)
(6.8) (6.9 )
(6.9 ) - динамикалық,
- динамикалық,  - гидростатикалық,
- гидростатикалық,  - статикалық (сыртқы) қысым деп аталады, ал олардың қосындысы толық қысым деп аталады. Демек, идеал сұйықтың стационарлы (қалыптасқан) ағысы кезінде түтік ағынының кез-келген қимасындағы толық қысым тұрақты шама.
- статикалық (сыртқы) қысым деп аталады, ал олардың қосындысы толық қысым деп аталады. Демек, идеал сұйықтың стационарлы (қалыптасқан) ағысы кезінде түтік ағынының кез-келген қимасындағы толық қысым тұрақты шама.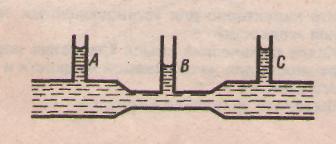
 ) Бернулли теңдеуі мына түрге келеді:
) Бернулли теңдеуі мына түрге келеді: (6.10)
(6.10)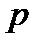 - дене бетіндегі сұйық қысымы. Ол қысым 6.5-суретте А түтікшенің көмегімен өлшенеді, толық қысым
- дене бетіндегі сұйық қысымы. Ол қысым 6.5-суретте А түтікшенің көмегімен өлшенеді, толық қысым  В түтікше көмегімен өлшенеді. Бұл кездегі статикалық қысым келесі өрнекпен анықталады:
В түтікше көмегімен өлшенеді. Бұл кездегі статикалық қысым келесі өрнекпен анықталады: 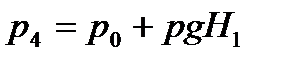 , мұндағы
, мұндағы  атмосфералық қысым, Н1 –А түтікшедегі сұйық бағанының биіктігі. В түтікшедегі қысым
атмосфералық қысым, Н1 –А түтікшедегі сұйық бағанының биіктігі. В түтікшедегі қысым  . Манометрлік түтікшедегі қысым айырымы
. Манометрлік түтікшедегі қысым айырымы (6.11)
(6.11) - сұйық деңгейлерінің айырымы. Екінші жағынан, Бернулли теңдеуіне сәйкес ағын түтігінің екі
- сұйық деңгейлерінің айырымы. Екінші жағынан, Бернулли теңдеуіне сәйкес ағын түтігінің екі  және
және  қималары үшін
қималары үшін  болғандықтан) келесі теңдік орынды
болғандықтан) келесі теңдік орынды
 , яғни
, яғни  (6.12)
(6.12)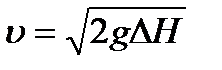 (6.13)
(6.13) , ал
, ал  - атмосфералық қысым.
- атмосфералық қысым. (6.14)
(6.14) (6.15)
(6.15) болса,
болса,  болады. Сондықтан
болады. Сондықтан  мүшесін ескермеуге болады. Сонда (6.15) – тең.
мүшесін ескермеуге болады. Сонда (6.15) – тең.  .
. (6.16)
(6.16) . Бұл (6.16) өрнек бірінші рет Торричелли алған. 6.6-суретте
. Бұл (6.16) өрнек бірінші рет Торричелли алған. 6.6-суретте  аз уақыт ішінде ыдыстан
аз уақыт ішінде ыдыстан  сұйық көлемі ағып өтеді. Соған сәйкес масса
сұйық көлемі ағып өтеді. Соған сәйкес масса 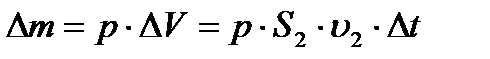 , мұндағы
, мұндағы  - сұйық тығыздығы. Ол
- сұйық тығыздығы. Ол  импульсқа ие.
импульсқа ие.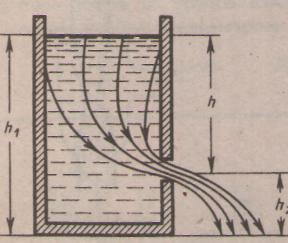
 массаға береді, яғни мынадай күшпен әсер етеді.
массаға береді, яғни мынадай күшпен әсер етеді.  .
. күш әсер етеді, яғни
күш әсер етеді, яғни (6.17)
(6.17)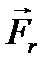 - ағатын сұйықтың реакция күші. Егер ыдыс арба үстінде тұрса, онда ол
- ағатын сұйықтың реакция күші. Егер ыдыс арба үстінде тұрса, онда ол 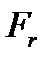 күштің әсерінен қозғалысқа келеді, ол реактивті қозғалыс деп аталады.
күштің әсерінен қозғалысқа келеді, ол реактивті қозғалыс деп аталады.







 ауданына және жылдамдықтың
ауданына және жылдамдықтың  градиентіне пропорционал болады, яғни
градиентіне пропорционал болады, яғни (6.18)
(6.18) тұтқырлық коэффициенті деп аталатын пропорционалды коэффициент. Оның өлшем бірлігі 1
тұтқырлық коэффициенті деп аталатын пропорционалды коэффициент. Оның өлшем бірлігі 1  . Тұтқырлық сұйықтың табиғатына және температурасына байланысты. Температураның өсуіне қарай тұтқырлық төмендейді.
. Тұтқырлық сұйықтың табиғатына және температурасына байланысты. Температураның өсуіне қарай тұтқырлық төмендейді.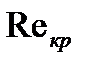 шамасымен анықталады:
шамасымен анықталады: (6.19)
(6.19)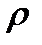 - сұйықтың тығыздығы,
- сұйықтың тығыздығы,  - түтік қимасы бойынша орташа ағыс жылдамдығы,
- түтік қимасы бойынша орташа ағыс жылдамдығы,  - түтік диаметрі.
- түтік диаметрі. кезінде ламинарлы ағыс, ал
кезінде ламинарлы ағыс, ал  кезінде турбулентті ағыс болып қалыптасады. Радиусы
кезінде турбулентті ағыс болып қалыптасады. Радиусы 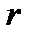 дөңгелек қимасы бар түтік үшін Рейнольдс саны
дөңгелек қимасы бар түтік үшін Рейнольдс саны  . Тұтқырлықтың әсері
. Тұтқырлықтың әсері  кезінде дөңгелек қимасы бар түтік бойынша әртүрлі қабаттардағы ағыс жылдамдықтары әртүрлі етіп жасалды. Оның орташа мәні Пуазейль өрнегі бойынша анықталады.
кезінде дөңгелек қимасы бар түтік бойынша әртүрлі қабаттардағы ағыс жылдамдықтары әртүрлі етіп жасалды. Оның орташа мәні Пуазейль өрнегі бойынша анықталады. (6.20)
(6.20) түтік радиусы,
түтік радиусы,  -түтік ұштарындағы қысым айырымы,
-түтік ұштарындағы қысым айырымы,  - оның ұзындығы.
- оның ұзындығы.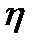 сұйық ішіндегі радиусы
сұйық ішіндегі радиусы 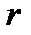 , жылдамдығы
, жылдамдығы  шар қозғалысына жасалатын кедергі күші мынаған тең:
шар қозғалысына жасалатын кедергі күші мынаған тең: (6.21)
(6.21) тұтқырлық коэффициентін анықтау үшін қолданылады.
тұтқырлық коэффициентін анықтау үшін қолданылады. ( 7.1 )
( 7.1 ) -тербеліп тұрған дененің (жүйенің) ығысуы, А – жүйенің тепе – теңдік күйден ең үлкен ауытқуы тербеліс амплитудасы,
-тербеліп тұрған дененің (жүйенің) ығысуы, А – жүйенің тепе – теңдік күйден ең үлкен ауытқуы тербеліс амплитудасы, 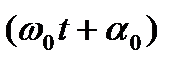 -
-  уақыт мезетіндегі тербеліс фазасы,
уақыт мезетіндегі тербеліс фазасы,  - бастапқы фазасы деп аталады. Фаза радиан немесе градус бірліктерінде өлшенеді,
- бастапқы фазасы деп аталады. Фаза радиан немесе градус бірліктерінде өлшенеді,  - циклдік жиілік, ол Т (бір период) уақыт ішіндегі болатын толық тербеліс санына тең шама.
- циклдік жиілік, ол Т (бір период) уақыт ішіндегі болатын толық тербеліс санына тең шама. рет тербелсе, онда
рет тербелсе, онда  ішінде
ішінде 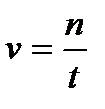 тербеліс жасайды, ал мұны тербеліс жиілігі деп атайды, ол периодқа кері шама
тербеліс жасайды, ал мұны тербеліс жиілігі деп атайды, ол периодқа кері шама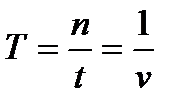 (7.2)
(7.2) (7.3)
(7.3) өлшенеді. Бір секундта бір тербеліс жасалатын болса, онда тербеліс жиілігі берге тең, оның өлшем бірлігі герц (Гц) деп аталады.
өлшенеді. Бір секундта бір тербеліс жасалатын болса, онда тербеліс жиілігі берге тең, оның өлшем бірлігі герц (Гц) деп аталады. және үдеумен
және үдеумен  сипатталады. Олардың мәндері (7.1) өрнегінен анықталады. (7.1) өрнегін уақыт арқылы дифференциалдап жылдамдық теңдеуін аламыз:
сипатталады. Олардың мәндері (7.1) өрнегінен анықталады. (7.1) өрнегін уақыт арқылы дифференциалдап жылдамдық теңдеуін аламыз: