 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГРАФИГІ МЕН ТАПСЫРУ МЕРЗІМІ 12 страница
8.5 сурет Бұл молекулалардың саны мынаған тең: n ∆S υ ∆t (n-молекулалардың концентрациясы). Бірақ, нақты жағдайда молекулалар ∆S аудаңға әртүрлі бұрыш жасап қозғалады және жылдамдықтары әртүрлі болады. Есептеуге оңай болу үшін молекулалардың хаосты, тәртіпсіз қозғалысын үш өзара перпендикуляр бағытпен ауыстырамыз. Кез-келген уақыт мезетінде әр бағытпен молекулалардың ескере отырып, газ молекулаларының ыдысқа түсіретін қысымын табамыз:
Егер газдың V көлеміндегі молекулалардың саны N болса, олардың қозғалыс жылдамдығы υ1, υ2, ... υN десек, онда газ молекулалары орташа квадраттық жылдамдықпен қозғалады деу орынды. Орташа квадраттық жылдамдық газ молекулаларының барлығының қозғаласын сипаттайды:
Сонда (8.11) теңдеуі (8.12) теңдеуін ескере отырып былай жазылады:
(8.13) өрнегі идеал газдардың молекулалық-кинетикалық теориясының негізгі теңдеуідеп аталады. Молекулалардың түрлі бағыттар бойынша хаосты қозғалысын ескеріп есептеу де (8.13) формуласына алып келді. Молекулалардың концентрациясы
немесе
Бір моль газ үшін
мұндағы
Менделеев-Клайперон теңдеуі бойынша
Молярлық масса мен бір молекуланың массасы арасындағы байланысты
Мұндағы Идеал газдың бір молекуласының ілгерілемелі қозғалысының орташа кинетикалық энергиясы
тек қана термодинамикалық температураға тәуелді. Бұл теңдеуден T=0 болғанда Бақылау сұрақтары: 1. Динамикалық зерттеу әдісі дегеніміз не? 2. Стаистикалық зерттеу әдісі, оның динамикалық зерттеу әдісінен айырмашылығы. 3. Статистикалық зерттеу әдісінің математикалық, физикалық негіздеріне қандай теориялық заңдылықтар алынған? 4. Термодинамикалық зерттеу әдісіне қандай заңдылықтар алынған? 5. Молекулалық теория құбылыстың қандай жақтарын зерттейді? 6. Идеал газ деп қандай газды айтамыз. 7. Идеал газ заңдарының анықтамалары мен формулаларын жазыңдар. 8. Молекула-кинетикалық теорияның негізгі теңдеуі және молекуланың ілгерілемелі қозғалысының орташа кинетикалық энергияларының формулаларын жазыңдар. ? Әдебиеттер: НӘ3,6 №9 дәріс Статистикалық таралулар Ықтималдық және флуктуация. Максвелл таралуы. Бөлшектердің жылулық қозғалысының жылдамдықтары. Сыртқы потенциалдық өрістегі бөлшектер үшін Больцман таралуы. Еркіндік дәреже саны. Еркіндік дәрежесі бойынша энергияның таралуы. Идеал газдың ішкі энергиясы. Идеал газдың жылу сыйымдылығы. Идеал газдың жылу сыйымдылығының молекула-кинетикалық теориясы және оның шектелуі. Максвелл таралуы. Бөлшектердің жылулық қозғалысының жылдамдықтары. Молекулалық-кинетикалық теорияның негізгі заңын қорытқан кезде молекулалар әртүрлі жылдамдықпен қозғалады дедік. Көптеген соқтығысулар нәтижесінде әр молекуланың жылдамдығы модулі және бағыты бойынша өзгереді. Бірақ молекулалардың хаосты қозғалуының нәтижесінде барлық қозғалыс бағыттары ықтимал, яғни орташа есеппен кез-келген бағытта қозғалатын молекулалар саны бірдей. Молекулалық-кинетикалық теория бойынша молекулалар соқтығысқанда жылдамдық қанша өзгергенімен газдағы массасы m0 молекуланың тепе-теңдік қалыпта тұрақты температурадағы Т= const орташа квадраттық жылдамдығы Молекулалардың жылдамдық бойынша таралу заңын қорытып шығарғанда Максвелл газ өте көп молекулалардан тұрады, молекулалар бірдей температурада тәртіпсіз жылулық қозғалыста болады және газға күш өрістері әсер етпейді деп алды. Максвелл заңы Егер молекулалардың жылдамдық диапазонын
Ықтималдылық теориясының әдістерін пайдалана отырып, Максвелл
(2.1) формуласынан көргендей
9.1 сурет Жылдамдығы
Идеал газдың жылдамдық бойынша таралу функциясы максимал мәнге ие болатын жылдамдықты ықтимал жылдамдық деп атайды. Ықтимал жылдамдықтың мәнін (9.1) формуласын жылдамдық бойынша дифференциалдап және нульге теңеп,
Егер температура жоғары болса, максимум оңға жылжиды,
9.2 сурет Таралу функциясы арқылы молекулалардың орташа арифметикалық жылдамдығын мына формуладан табады:
Газ күйін сипаттайтын жылдамдықтар: 1) ықтимал жылдамдық - 2) орташа арифметикалық жылдамдық - 3) орташа квадраттық жылдамдық - Молекулалардың жылдамдық бойынша үлестірілуінен газ молекулаларының кинетикалық энергия бойынша үлестірілуі функциясын алуға болады.
Ол үшін (9.4) формуласындағы айнымалы жылдамдық
Мұндағы
Идеал газдың орташа кинетикалық энергиясын таралу функциясын пайдаланып табуға болады:
Сыртқы потенциалдық өрістегі бөлшектер үшін Больцман таралуы. Барометрлік формула. Молекулалық-кинетикалық теорияның негізгі теңдеуі бойынша және Максвелл таралу заңы бойынша газ молекулаларына сыртқы күштер әсер етпейді, сондықтан олар көлемде бірқалыпты таралады деп есептелінді. Бірақ кез-келген газдың молекуласы Жердің тартуының потенциалдық өрісі әсерінде болады. Ауырлық күші мен молекулалардың жылулық қозғалысы газдың стационар күйіне әкеледі, газ қысымы биіктікке байланысты азаяды. Тартылыс өрісін біртекті, температура тұрақты және барлық молекулалардың массасы бірдей деп алып, қысымның биіктікке байланысты өзгерісін көрсететін заңды қорытайық (9.3 сурет). Егер h биіктікте атмосфералық қысым p-ға тең болса, онда h + dh биіктікте ол p+dp –ға тең (dh >0 болғанда dp<0, себебі қысым биіктікпен азаяды). 9.3 сурет Қысымның биіктікке байланысты өзгерісін көрсететін заңды қорытқанда, өріс біртекті, температура тұрақты және барлық молекулалардың массасы бірдей деп аламыз. Егер h биіктікте атмосфералық қысым р-ға тең болса, онда h+dh биіктікте ол p+dр-ға тең (dh>0 болғанда dр>0 , себебі қысым биіктікпен азаяды) p және р+ dр қысымының айырмасы биіктігі dh-қа тең цилиндрдің көлемінің ішіндегі газдың салмағына тең p-(p+dp)= ρgdh, ρ-газдың тығыздығы, dh- өте аз биіктік болғандықтан газдың тығыздығын өзгермейді, тұрақты деп алуға болады. Сондықтан dр = - ρgdh (9.7) Идеал газдың күй теңдеуін пайдалана отырып, тығыздықты табамыз Бұл формуланы (9.7) ге қойып, мынаны аламыз
немесе Биіктік h1-ден h2-ге өзгергенде қысымда р1-ге ден р2-ге өзгереді, яғни
немесе
Алынған формула барометрлік формула деп аталады, ол биіктікке байланысты атмосфералық қысымды табуға немесе қысымды өлшеп алып, сол арқылы биіктікті табуға мүмкіндік береді. Биіктік теңіз деңгейіне қатысты өзгереді. Сондықтан (9.8) формуласын
деп жазуға болады, мұндағы р - h биіктіктегі қысым. Биіктікті өлшейтін құралды альтиметр деп атайды. Альтиметрдің жұмысы (9.9) формуласын қолдануға негізделген. Бұл формула газ ауыр болған сайын оның қысымы биіктікке байланысты тез кемитінін көрсетеді. Барометрлік формуланы р=nkТ өрнегін пайдаланып былай жазуға да болады:
п - h биіктіктегі молекулалардың концентрациясы, n0 - h=0 биіктіктегі молекулалардың концентрациясы.
деп жазуға болады, m0gh=П- молекуланың потенциалдық энергиясы екенін ескеріп, (9.10) өрнегін мына түрде жазуға болады:
(9.11) формуласы сыртқы потенциалдық өрістегі Больцман таралуы деп аталады. Тұрақты температурада Т=const молекуланың потенциалдық энергиясының кемуіне сол жердегі газ тығыздығының көбеюі сәйкес келеді. Жылулық хаосты қозғалыстағы молекулалардың массалары бірдей болса, Больцман таралуы тек қана ауырлық күші өрісінде емес, сыртқы потенциалдық өрісте де орынды. Молекуланың орташа соқтығысу саны және еркін қозғалысының орташа ұзындығы. Газ молекулалары жылулық тәртіпсіз қозғалыс әсерінен бір-бірімен соқтығысады. Екі соқтығыс аралығында молекула L жол жүреді, молекуланың еркін қозғалыс кезіндегі екі соқтығыс арасында жүрген жолы - еркін қозғалыс жолының ұзындығы деп аталады. Жалпы жағдайда әр соқтығыс арасындағы жүрілген жол әртүрлі болады, хаосты қозғалатын молекулалар саны өте көп болғандықтан, молекулалардың еркін қозғалысының орташа жолы туралы айтуға болады Соқтығысқанда молекуланың центрі жақындайтын ең кіші арақашықтықты молекуланың эффективті диаметрі d деп атайды (9.4 сурет). 9.4 сурет Молекуланың эффективті диаметрі соқтығысушы молекулалардың жылдамдығына тәуелді, демек температураға да тәуелді. 1 с ішінде молекула орташа арифметикалық жылдамдыққа тең
Соқтығыс санын 9.5 сурет 1с ішіндегі соқтығысу саны «сынық» цилиндрдің ішіндегі молекулалар санына тең:
мұндағы n - молекулалардың концентрациясы десек, Басқа молекулалардың қозғалысын есептесек орташа соқтығыс саны мынаған тең:
Сонда еркін қозғалыстың орташа ұзындығын төмендегі өрнек арқылы анықтауға болады:
Идеал газдың ішкі энергиясы. Еркіндік дәреже саны. Еркіндік дәрежесі бойынша энергияның таралуы. Термодинамикалық жүйенің ең маңызды сипаттамаларының бірі ішкі энергия U болып табылады. Ол жүйедегі микробөлшектердің (молекула, атом, электрон, ядро, т.б.) хаосты (жылулық) қозғалысының және осы бөлшектердің өзара әсерлесу энергиясы болып табылады. Біртұтас жүйенің қозғалысының кинетикалық энергиясы мен сыртқы өрістегі жүйенің потенциалдық энергиялары ішкі энергия болып есептелінбейді. Ішкі энергия – жүйенің термодинамикалық күйінің функциясы, демек жүйенің әр күйде белгілі бір ішкі энергиясы болады. Жүйе бір күйден екінші бір күйге өткенде оның ішкі энергиясының өзгерісі сол күйлердің ішкі энергияларының айырмасымен анықталады: Еркіндік (еріктілік) дәрежелер саны деп жүйенің кеңістіктегі орнын толықтай анықтайтын тәуелсіз айнымалылар (координаталар) санын айтады. Мысалы, көптеген есептерде бір атомды газ молекуласын ілгерілемелі қозғалыстың үш еркін дәрежесі бар материялық нүкте ретінде қарастырады да, айналмалы қозғалыстың энергиясы ескерілмейді: і = 3. Суретте а) жағдайы (
Поиск по сайту: |
 бөлігі қозғалады, олардың жартысы
бөлігі қозғалады, олардың жартысы 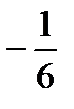 бөлігі берілген бағытпен бір жаққа, қалған жартысы қарсы бағытта қозғалады. Берілген бағытта қозғалып, ∆S аудаңға соқтығысатын молекулалардың саны
бөлігі берілген бағытпен бір жаққа, қалған жартысы қарсы бағытта қозғалады. Берілген бағытта қозғалып, ∆S аудаңға соқтығысатын молекулалардың саны 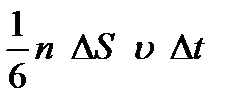 -ға тең болады. Молекулалардың соқтығыс кезінде ауданға беретін импульсін:
-ға тең болады. Молекулалардың соқтығыс кезінде ауданға беретін импульсін:  ,
, . (8.11)
. (8.11)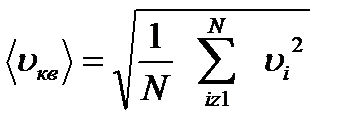 (8.12)
(8.12) (8.13)
(8.13) екенін ескере отырып, төмендегі формуланы аламыз:
екенін ескере отырып, төмендегі формуланы аламыз: (8.14)
(8.14)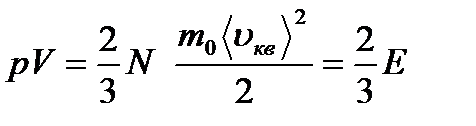 (8.15) Мұндағы Е - газдың барлық молекулаларының ілгерілемелі қозғалысының кинетикалық энергиясының қосындысы. Газдың массасы
(8.15) Мұндағы Е - газдың барлық молекулаларының ілгерілемелі қозғалысының кинетикалық энергиясының қосындысы. Газдың массасы 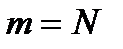 m0 екенін ескеріп, (8.14) теңдеуін былай жазуға болады:
m0 екенін ескеріп, (8.14) теңдеуін былай жазуға болады: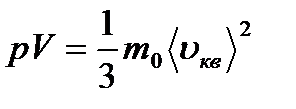
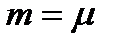 , сондықтан
, сондықтан
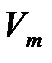 - молярлық көлем.
- молярлық көлем.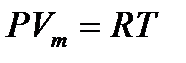 өрнегін пайдаланып, орташа квадраттық жылдамдықты табамыз.
өрнегін пайдаланып, орташа квадраттық жылдамдықты табамыз.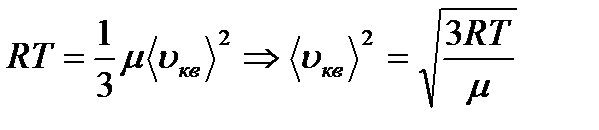 (8.16)
(8.16) ескере отырып, (8.16) теңдеуін мына түрде жазуға болады:
ескере отырып, (8.16) теңдеуін мына түрде жазуға болады: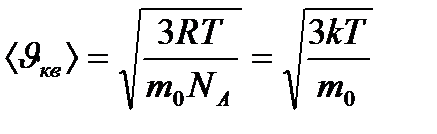 (8.17)
(8.17)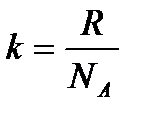 - Больцман тұрақтысы,
- Больцман тұрақтысы, 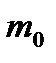 - бір молекуланың массасы,
- бір молекуланың массасы, 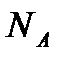 - Авогадро тұрақтысы. Осы өрнек арқылы есептесек, бөлме температурасындағы оттегі молекулаларының орташа жылдамдығы 480 м/с, сутегі молекулаларының орташа жылдамдығы 1900 м/с болады. Ал сұйық гелий температурасында оттегі және сутегі молекулаларының орташа квадраттық жылдамдықтары 40 және 160 м/с тең.
- Авогадро тұрақтысы. Осы өрнек арқылы есептесек, бөлме температурасындағы оттегі молекулаларының орташа жылдамдығы 480 м/с, сутегі молекулаларының орташа жылдамдығы 1900 м/с болады. Ал сұйық гелий температурасында оттегі және сутегі молекулаларының орташа квадраттық жылдамдықтары 40 және 160 м/с тең. (8.18)
(8.18)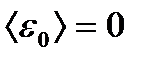 екендігі, демек 0 К температурада газ молекуласының ілгерілемелі қозғалысы тоқталатынын, оның қысымының нольге тең болатынын көрсетеді. Термодинамикалық температура идеал газ молекулаларының ілгерілемелі қозғалысының орташа кинетикалық энергиясының өлшемі болып табылады және (8.8) формуласы температураны молекулалық- кинетикалық тұрғыдан түсіндіреді.
екендігі, демек 0 К температурада газ молекуласының ілгерілемелі қозғалысы тоқталатынын, оның қысымының нольге тең болатынын көрсетеді. Термодинамикалық температура идеал газ молекулаларының ілгерілемелі қозғалысының орташа кинетикалық энергиясының өлшемі болып табылады және (8.8) формуласы температураны молекулалық- кинетикалық тұрғыдан түсіндіреді. тең. Мұны былай түсіндіруге болады: Т= const болғанда тепе-теңдік күйдегі газда уақыт уақыт бойынша өзгермейтін молекулалардың жылдамдық бойынша таралуы, яғни стационар таралуы орын алады. Ол белгілі бір статистикалық заңға бағынады, теория жүзінде ол заңды қорытып шығарған Дж. Максвелл.
тең. Мұны былай түсіндіруге болады: Т= const болғанда тепе-теңдік күйдегі газда уақыт уақыт бойынша өзгермейтін молекулалардың жылдамдық бойынша таралуы, яғни стационар таралуы орын алады. Ол белгілі бір статистикалық заңға бағынады, теория жүзінде ол заңды қорытып шығарған Дж. Максвелл.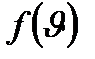 функциясымен сипатталады, ол функция молекулалардың жылдамдық бойынша таралу функциясы деп аталады.
функциясымен сипатталады, ол функция молекулалардың жылдамдық бойынша таралу функциясы деп аталады. -ға тең кіші интервалдарға бөлсек,онда жылдамдықтың әрбір интервалына
-ға тең кіші интервалдарға бөлсек,онда жылдамдықтың әрбір интервалына 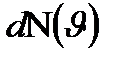 молекулалар саны келеді,
молекулалар саны келеді, 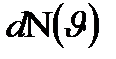 молекулалардың жылдамдығы осы интервалда жатады.
молекулалардың жылдамдығы осы интервалда жатады.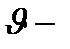 дан
дан  интервалында жатқан молекулалардың салыстырмалы санын анықтайды:
интервалында жатқан молекулалардың салыстырмалы санын анықтайды:  , яғни
, яғни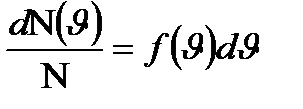 бұдан
бұдан 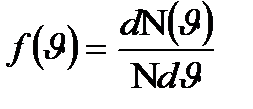 .
.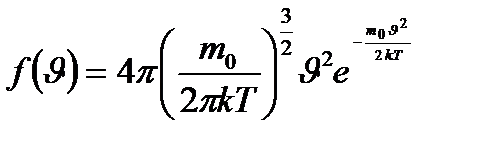 (9.1)
(9.1)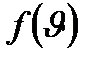 функциясы газдың массасына және температураға Т тәуелді.
функциясы газдың массасына және температураға Т тәуелді.  өскен сайын
өскен сайын 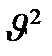 -на қарағанда
-на қарағанда 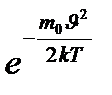 тез азайса, онда
тез азайса, онда  тең болғанша өседі,
тең болғанша өседі, 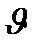 =
=  болғанда максимумға жетеді, сосын асимптотикалы нульге ұмтылады. Қисық
болғанда максимумға жетеді, сосын асимптотикалы нульге ұмтылады. Қисық 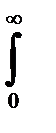
 = 1
= 1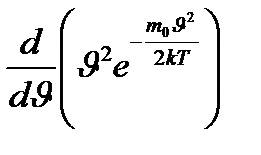 = 2
= 2 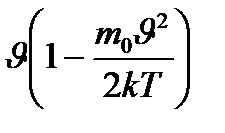
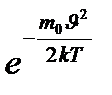 = 0
= 0 92.1) өрнегінің минимум шартына сәйкес келеді, жақша ішіндегі өрнек нульге тең болатын болса, ықтимал жылдамдықтың
92.1) өрнегінің минимум шартына сәйкес келеді, жақша ішіндегі өрнек нульге тең болатын болса, ықтимал жылдамдықтың 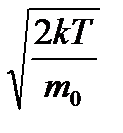 =
= 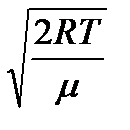 (9.2)
(9.2)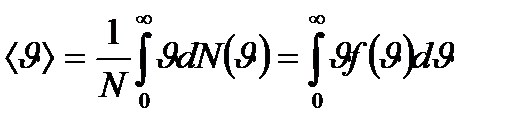
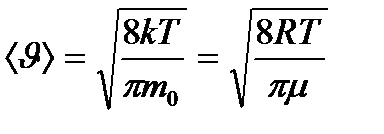 (9.3)
(9.3)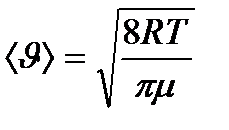 ,
,  ;
;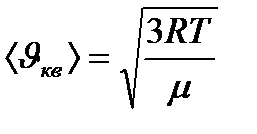 ,
,  .
.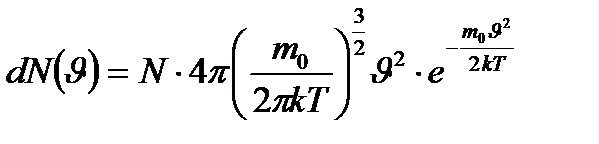 (9.4)
(9.4) шамасынан кинетикалық энергия
шамасынан кинетикалық энергия  шамасына көшу қажет:
шамасына көшу қажет:  ,
, 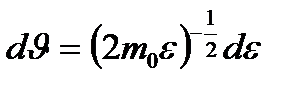 . Сонда (9.4) формуласын мына түрде жазуға болады:
. Сонда (9.4) формуласын мына түрде жазуға болады: ;
;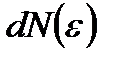 -
- 
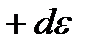 интервалындағы ілгерілемелі қозғалыстың кинетикалық энергиясы бар молекулалар саны. Сонымен, молекулалардың жылулық қозғалысының энергиясы бойынша таралу функциясының өрнегін жазайық:
интервалындағы ілгерілемелі қозғалыстың кинетикалық энергиясы бар молекулалар саны. Сонымен, молекулалардың жылулық қозғалысының энергиясы бойынша таралу функциясының өрнегін жазайық:
 . (9.5)
. (9.5)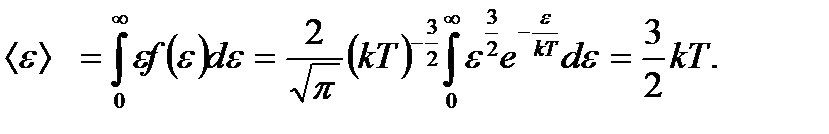
 ,
,
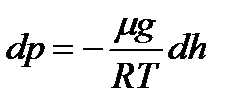 ,
,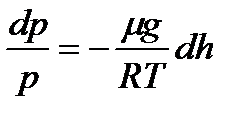

 ,
,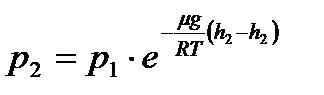 (9.8)
(9.8) (9.9)
(9.9)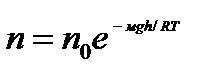
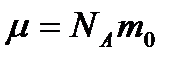 және
және 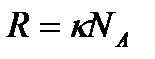 болғандықтан
болғандықтан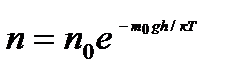 (9.10)
(9.10) (9.11)
(9.11)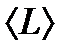 .
.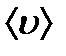 жол жүрсе және
жол жүрсе және 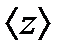 - 1 с ішіндегі бір молекуланың орташа соқтығыс саны болса, онда еркін қозғалыстың орташа ұзындығы
- 1 с ішіндегі бір молекуланың орташа соқтығыс саны болса, онда еркін қозғалыстың орташа ұзындығы (9.12)
(9.12)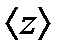 - ті анықтау үшін молекуланы диаметрі d-ға тең шар деп алайық, ол қозғалмайтын басқа молекулалардың арасында қозғалсын. Бұл молекула тек қана центрі d-ға тең немесе одан аз қашықтықта орналасқан молекулалармен соқтығысады, яғни «сынық» (радиусы d-ға тең) цилиндрдің ішінде орналасқан молекулалармен соқтығысады (9.5 сурет).
- ті анықтау үшін молекуланы диаметрі d-ға тең шар деп алайық, ол қозғалмайтын басқа молекулалардың арасында қозғалсын. Бұл молекула тек қана центрі d-ға тең немесе одан аз қашықтықта орналасқан молекулалармен соқтығысады, яғни «сынық» (радиусы d-ға тең) цилиндрдің ішінде орналасқан молекулалармен соқтығысады (9.5 сурет).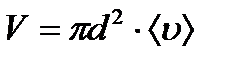 , ал <υ>- молекулалардың орташа жылдамдығы немесе 1 с ішінде жүрілген жол. Сонымен орташа соқтығыс саны
, ал <υ>- молекулалардың орташа жылдамдығы немесе 1 с ішінде жүрілген жол. Сонымен орташа соқтығыс саны 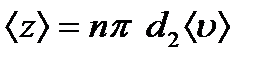
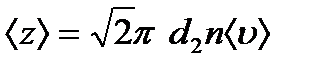
 (9.13)
(9.13)
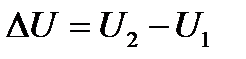 . Жүйенің ішкі энергиясының өзгерісі жүйе бір күйден екінші күйге қандай жолмен келгеніне тәуелсіз шама болып табылады.
. Жүйенің ішкі энергиясының өзгерісі жүйе бір күйден екінші күйге қандай жолмен келгеніне тәуелсіз шама болып табылады.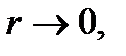
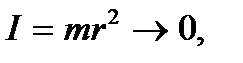
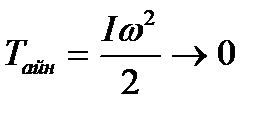 ).
).