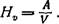|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Критерии прочности при статической нагрузкеСтр 1 из 19Следующая ⇒
Таблица 3
Если ограничиться глубинами, достигнутыми современными рудниками (около 2 км), то на основании вышеизложенного можно считать, что влияние давления на плотность горных пород с глубиною весьма незначительно и в первом приближении может считаться отсутствующим. Для таких глубин можно считать, что объем породы до деформации и после остается постоянным. Это, однако, нельзя распространить на сыпучие породы, грунты и вообще глинистые породы, для которых плотность заметно изменяется с изменением давления. § 14. Упругость Горные породы при нагрузках, не превышающих определенных величин, обладают упругостью. Однако__они не являются телами вполне упругими. По снятии нагрузки они™ обнаруживают упругое последействие и остаточные деформации. Упругие свойства горной породы во многом зависят от упругих свойств составляющих ее кристаллов. В кристалле упругие свойства меняются в зависимости от направлений. Для полной характеристики упругого состояния кристалла в общем случае нужно определить 21 упругую постоянную. Симметрия позволяет это число уменьшить для кристаллов кубической син- гонии до трех, для ромбической сингонии — до шести и т. д. Линейчый-ааирд^шкшюсак напряжений, & деформаций в оддо&ъ лах*У£пругой области не соблюдается. Предел упругости, опреде- Ляемыйопытом, не представляет постоянной величины. Он зависит от степени точности измерений при опыте, а также от промежутка времени действия приложенной нагрузки. В табл. 4 даны значения предела упругости для кристаллов каменной соли при комнатной температуре в зависимости от способа определения (по В. Д. Кузнецову [9]). Таблица 4
В простой горной породе зерна имеют различные формы, размеры, ориентировку и характер контактов между собою. При простом напряженном состоянии такого поликристаллического агрегата каждое зерно, не принадлежащее поверхности, оказывается в объемном напряженном состоянии. Деформации таких зерен препятствуют окружающие их и связанные с ними зерна. Различная ориентировка зерен по отношению к направлению действующего внешнего усилия создает в каждом зерне самостоятельные соотношения между напряжениями и в частности определяет в каждом из зерен свое время появления первоначальных сдвигов. Предел упругости в каждом из зерен будет достигнут вообще в разное время, и для агрегата в целом этот предел будет повышенным. Зависимость между напряжениями и деформациями оказывается криволинейной. В сложной горной породе положение вещей еще более услож- няётсяГЗд^сь каждый из_компонёнтов имеет свой предел упругост.и. Взаимодействие компонентов агрегата при деформации определяется сцеплением их между собой и с цементом. До тех пор, пока сцепление в отдельных точках агрегата не нарушено, все компоненты работают под влиянием внешней нагрузки совместно. В результате получаются одинаковые деформации компонентов и цемента в контактах. Однако при этом в направлениях, отличных от направления действующего усилия, возникают различные по величине напряжения. Отсюда — неравномерность напряженного состояния агрегата. Эта неравномерность еще более усиливается, когда в процесс включаются мелкие осколки и частицы (по существу — сыпучие тела), получающиеся при разрушении отдельных, относительно слабых зерен в агрегате, предел прочности которых был превзойден при постепенном увеличении нагрузки. Получаемые при этом диаграммы „напряжение-деформация" отражают вообще некоторые средние переменные характеристики упругих свойств. В табл. 5 даны средние значения модуля упругости и коэфнциента Пуассона для некоторых горных пород, испытанных при вростых напряженных состояниях. Ш Т а бЖи ца 5
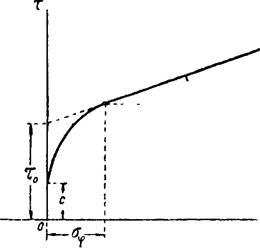
Для простых и сложных пород н вообще для поликристаллических агрегатов типично явление релаксации Горные породы включают кристаллы и примеси с различной способностью к деформированию. Кроме того, они имеют поры и трещины. Все это при нагрузке приводит к неоднородному напряженному состоянию. По удалении нагрузки упруго деформированные зерна стремятся восстановить свою форму. Однако этому могут препятствовать кристаллы и примеси, предел упругости которых при нагрузке был превзойден. Преодоление этнх препятствий и составляет в простейшем представлении явление релаксации. Вообще же релаксация — явление постепенного уменьшения напряжения при постоянстве деформации, наблюдаемое по приложении к телу снлы, превосходящей некоторый предел, и затем постепенно уменьшаемой с асимптотическим приближением к некоторому пределу. Подробнее об этом — в § 15. Числовые значения упругих характеристик, подобные приведенным в табл. 5 и получаемые при помощи обычных лабораторных испытаний, позволяют лишь весьма отдаленно судить об упругих свойствах тех же пород, но находящихся в массиве, т. е. в условиях объемного напряженного состояния. Данные сейсмометрии показывают, что в нетронутом массиве гор ные породы обладают повышенными упругими характеристиками. Средние значения модуля упругости, вычисляемые по скорости распространения продольных волн, оказываются большими, чем вычисляемые на основании испытаний статическими методами. Так, например, модуль упругости гранита при динамическом методе, когда в образце возбуждались продольные волны, оказался больше модуля упругости, вычисляемого на основании статических методов, приблизительно на 20% [6] Возьмем единичный объем породы в форме кубика, считая породу однородной и изотропной. При простом сжатии этого кубика силою рх будем иметь продольное сжатие в пределах упругости равным г—El El ' где Et — модуль упругости при простом сжатии. Поперечное же расширение кубика при этом будет ei = fi.e, где fi — коэфнциент Пуассона. Рассмотрим теперь тот же кубик породы, но в условиях массива, и при том же давлении сверху рх. Здесь поперечному расширению будет препятствовать окружающая порода и, таким образом, вх=0. Это равносильно приложению по бокам кубика некоторых усилий Р1, компенсирующих расширение е1. Результирующая деформация по какому-либо боковому направлению будет: р'\ рх pi л откуда P'^T~-Pv 0.14) При этом величина продольного сжатия составит: , pi pi pi pi 2р\ Подставляя сюда значение р\ из (1,14), получим: Pi V „ - Pi (14- ц)(1 — 2ц) Ех (1 -tfE^Pi-Ei 1-ц Из этого выражения следует, что модуль упругости при сжатии в одном направлении и отсутствии бокового расширения равен: Е° " <1+^)(1-2ц)'(2«14) Для большинства горных пород в среднем fi = 0,25. Подставляя это значение р в (2,14), получим £0=* 1,20 Ev что, в частности, совпадает с приведенными выше данными для гранита. Из (2,14) следует, что в условиях массива модуль упругости зависит только от физического состояния породы и не зависит от глубины. 9 15. Пластичность и хрупкость;* Пластичность твердого тела может быть определена как способность его поглощать, не разрушаясь, механическую энергию в необратимой форме. В последнее время предложено рассматривать пластичность более широко, а именно—как совокупность свойств реадьр ных твердых тел, определяющих йТ~сотфотнвле1П1е^и спосоддош» дефрщшвоваться включительно до_разрушМия_д_Ж№им^001Д8- р актер а нагрузок, времени и скоро сТйюГдействия и температурных "условий [ 10]. "При этом определении в понятие пластичности, как "видноГвкяючается и понятие упругости. При пластическом состоянии твердое тело под влиянием нагрузки способно давать остаточную деформацию. Наоборот, хрупкость — состояние твердого тела, при котором оно под действием нагрузки неспособно давать остаточную деформацию, имея предел прочности весьма близким к пределу упругости. Состояния пластичности и хрупкости определяются взаимодействием следующих факторов: структуры тела, размеров и формы зерен, гранулометрического состава, дефектов и искажений, относящихся к самим зернам (решетке их), поверхности их и к веществу, связывающему зерна, температуры и времени действия сил. Несмотря на обилие экспериментального и опытного материала, еще не установлена окончательно физическая сущность хрупкости и пластичности. В этом отношении имеются пока гипотезы. Все кристаллы независимо от характера междуатомной связи обладают пластическими свойствами. Эти последние оказываются весьма чувствительными к особенностям структуры и сильно зависят от примесей и предшествовавшей деформации. В отношении кристаллов известны гипотезы: теплоных флюктуаций, неоднородности, дислокации и др. [11]. Не рассматривая этих гипотез, остановимся на гипотезе А. Ф. Иоффе, предложенной для поликристаллического вещества [12]. По А. Ф. Иоффе, хрупкая прочность каменной соли <зт не зависит или же находится в слабой зависимости от температуры. На диаграмме „температура-напряжение" линия от вполне или почти параллельна оси температур (фиг. 5). Что же касается предела текучести as, то он понижается с увеличением температуры. Линии аг и as в пересечении дают критическую точку, ниже которой имеет место пластическое, а выше— хрупкое состояние. Для каменной соли эта точка отвечает приблизительно 200°. Независимость хрупкой прочности от температуры была получена в интервале от температуры жидкого воздуха до 700°. Данная гипотеза во многих случаях была подтверждена опытом. Более сложен вопрос о влиянии времени. Палочка сургуча, поло-_ женная на две опоры, с течением времени пластически прогибается под влиянием собственного веса. Та же палочка, но при ударе, разрушается хрупким образом. Твердый асфальт при ударе разрушается хрупко, а, будучи оставлен на продолжительное время в бочке со щелями, способен вытекать из нее. Образование складок и вообще многие горообразовательные процессы, протекающие весьма медленно, связаны с пластичностью горных пород. Для объяснения этих явлений может до некоторой степени служить теория твердого тела, согласно которой [13]
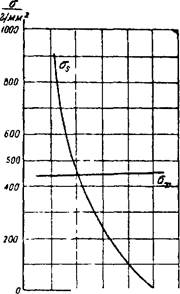
Р = + (1,15) где: р — напряжение; Л — модуль упругости; х — элемент деформации; ц — коэфнциент вязкости; t— время. Из формулы (1,15) видно, что при быстром увеличении деформации второй член правой части получает большое значение. При этом напряжение р быстро подходит к пределу прочности или его превышает. Получается -хрупкое разрушение тела. Наоборот, при медлен- к ном возрастании деформации получается медленное „течение" тела —пластическая де- __________________ формация. „Течение" твердого тела имеет место вообще при не- \fftff) котором постоянном напряже- 0 s нии. При этом с течением времени деформация увеличивается. На фиг. 6 дана диаграмма -------------------------------------------------- £ деформации идеального упруго-пластического тела. Част- Фиг. 6. Деформация ид-ального упруго-пласти- ным Случаем его является ческого тела. идеальное пластическое тело (фиг. 7). Для реального упруго-пластического тела (горной породы) явление усложняется. При постоянстве деформирующей силы скорость роста пла- -г ---------------------- стической деформации посте- ! пенно уменьшается, прибли- I жаясь к нулю. Для продол ен жения деформации нужно по- ! степенно увеличивать напря жение. В результате диаграмма деформации получает вид ------------------- _—--------- g как на фИ1Ч g или, схемати- Фиг. 7. Деформация идеального пластического чески, как на фиг. 9. Явление тела- постепенного увеличения де формации, обязанного соответствующему увеличению напряжения, носит название упрочнения тела в процессе пластической деформации. На фиг. 9 как упругая, так и пластическая деформации изменяются по линейному закону: (2,15) Здесь h — коэфнциент упрочнения тела, оцениваемый тангенсом угла наклона участка пластической деформации а к оси е. Уравнение (2,15) представляет собою^ некоторое приближение к действительному положению вещей, обычно отображаемому для реальных тел, и в частности для горных пород, диаграммой, как на фиг. 8. С пластической деформацией связано явление релаксации. По В. Д. Кузнецову, эта последняя представляет одно из проявлений течения вещества, которое происходит без видимого изменения его фермы. Течение это заключается в том, что первоначальное упруго- напряженное состояние тела переходит в более равновесное состояние. При этом упругая деформация уменьшается, а пластическая возрастает, но полная деформация остается неизменной. Релаксация Горные породы, простые и сложные, обладают пластичностью, которая особенно типично проявляется при длительном действии сил. Подробно пластическая де- с формация горных пород рассматривается в главе IV Деформация горных пород вообще отвечает диаграмме на фиг. 8. Исключение составляют глины и вообще тонкодисперсные породы (землистые и т. п) Такие породы способны образовывать с водою тестообразные массы, дающие пластичный поток. Было Фиг. 8. Деформация реального упруго-пластиче- предложено следующее об- ского тела,
щее уравнение такого потока [14]:
Здесь F— тангенциальное усилие, действующее на площади S; G — модуль сдвига, Т — время релаксации (Г—-ц G), 7 — упругая деформация; i\ — вязкость; ^ - градиент скорости; в — предел упругости при сдвиге. а
---'Л
п
Фиг 9 Упрощенная диаграмма „напряжение — деформация' для реальных упруго-пластических тел Из этого уравнения могут быть получены следующие частные случаи- 0 — уравнение вязкости Ньютона, dv :7i-Tz
т dF б) при ^7=0 и Gf-О, уравнение пластичного потока
6=0,
vfs. iS^r T AW в) при ^-«О и 0 =»0, уравнение, идентичное уравнению (1,15); у-Ot-4S-0, г) при-^-- ^ = 0, к) 0 и 8=0, линейный закон для упругого тела В технике пластичность глин и вообще грунтов оценивается двумя показателями: нижним пределом пластичности и нижним пределом текучести. Первый представляет собою процентное содержание воды в грунте, при котором последний перестает раскатываться в тонкий непрерывный шнур, а второй—процентное содержание, при котором обе половинки образца грунта при сотрясении соединяются в одно целое. Разность между этими показателями составляет так называемое число пластичности. Для грунтов в плывучем состоянии число пластичности равно нулю, а для очень плотных глин—15. § 16. Твердость Твердость — способность тела сопротивляться прониканию в него другого тела (при опытах—в виде острого наконечника), не получающего остаточной деформации. Это—часто применяемое в технике определение твердости. Это определение лежит в основе известной шкалы Мооса, применяемой для определения относительной твердости минералов. Шкалой Мооса отчасти можно пользоваться и для оценки относительной твердости простых горных пород. Сложнее обстоит вопрос с определением твердости неоднородных по составу и вообще сложных горных пород. Были предложены различные способы оценки твердости таких пород: способ сверления, способ с отскакиаанием стального шарика и др. Однако все они не получили сколько-нибудь широкого применения. До некоторой степени показательным является следующий способ: процентное содержание каждого минерала в данной сложной породе умножается на показатель твердости этого минерала по шкале Мооса и сумма полученных произведений делится на 100. Таблица 6
В табл. 6 приведены показатели твердости некоторых горных пород (с содержанием кварца), полученные указанным способом. Из изложенного следует, что твердость горной породы может оцениваться различными способами. Получаемые при этом результаты, конечно, не могут быть сравниваемы между собою. Таким образом, определяемая тем или иным способом твердость породы не представляет собою определенного, присущего данному телу, физического свойства. Это скорее, по выражению В. Д. Кузнецова,—.результат некоторых операций с материалом, произведенных с определенными приборами" [9]. В последнее время понятие о твердости тела работами П. А. Ре- биндера, В- Д. Кузнецова и др. значительно уточнено. По определению П. А. Ребиндера, твердость — сопротивляемость твердого тела разрушению, измеряемая энергией, которая затрачивается на образование единицы поверхности тела, возникающей в данном процессе его разрушения [15]. Из этого определения следует, что твердость тела может быть выражена так: н — А s Д5 > где А—работа разрушения, в результате которой получено увеличение поверхности Д5. Процессы разрушения твердого тела необратимы. Поэтому работа А, затрачиваемая на разрушение тела, вообще больше работы Av действительно необходимой для образования свободной поверхности Д5. Необратимая часть работы q в общем случае состоит из: qx— работы, запасаемой в виде энергии упругих деформаций, qt—работы на пластические деформации и q3 — работы, затрачиваемой на треиие, не сопровождающееся разрушением. Таким образом: A — A1-\-q = A1Jrql-\-q^Jrq3. (а) Если свободная поверхностная энергия — X и Д5 — образованная поверхность раздела, то Л, =Х.Д5. В простейшем случае можно предположить, что имеет место приближенная пропорциональность между твердостью Н и X (Ребин- дер), т. е. Я «АХ, или, так как A = HbS=X.-AS-\-q, то и 55 =(*-!)*. Здесь величина k может быть названа коэфициентом необратимости данного процесса разрушения тела. Обычно Л>1, и только при полной обратимости процесса k—\. Для одного и того же процесса разрушения, проводимого с различными телами, коэфнциент k оказывается приблизительно постоянным (Ребиндер). Обращаясь к выражению (а), отметим, что обычно значение q достаточно велико по сравнению с Av Однако в случае горных пород, добыча (разрушение) которых производится преимущественно с помощью ударного действия (когда практически порода оказывается хрупкой), член q2 можно считать малым по сравнению с qu а член qs — не имеющим существенного значения, в особенности для забоев ^ .'Vj '-у gf*- wr ^ ya-^t"? v-^ в горизонтальных и восстающих выработках. Таким «браком, для указанных условий можно считать В последующем для оценки твердости Н всюду принимается полная работа А, затрачиваемая в процессе разрушения, т. е. вместо принимается // = ~ (^ = 0). По существу, это, конечно, не точно. Однако в случаях, когда оценка твердости производится для горных пород одного и того же минерального состава (например, для каменного угля), то член можно считать приблизительно постоянным и тогда Н — + const представит собою несколько повышенное, по сравнению с истинным, значение твердости. Работа разрушения А может быть отнесена и к единице объема разрушаемого тела, и тогда выражение твердости будет:
Между Нь и Hv существует такая связь: HsbS=Hv-V, откуда Hv~Hsy- Отношение ^ представляет собою удельную поверхность или степень измельчения тела (породы) при разрушении—важную характеристику измельченного продукта. Обозначая эту величину через (3, получим: и, подставляя сюда значение Hv, будем иметь: н -1 Л ns~ р ' V • Твердость Hs или Hv имеет определенную размерность. Она зависит от вида того процесса увеличения поверхности, в котором она определяется. Поэтому сравнение между собою значений Hs или Hv возможно лишь для однородных в механическом отношении процессов разрушения твердого тела. При разных способах разрушения данного твердого тела числовые значения Hs или Hv при всех прочих одинаковых условиях будут, вообще говоря, различными. Таким образом, и новое определение твердости не дает однозначной числовой оценки этого свойства твердого тела. Тем не менее, это определение можно использовать для практических приложений. Пользуясь им, автор настоящего труда сделал попытку построения теории добываемости горных пород, во многом оправдываемой опытом. Изложение этой теории составляет содержание главы IX. § 17. Разрыхляемость Разрыхляемость — увеличение объема добытой горной породы по сравнению с объемом ее в массиве. Это свойство горных пород имеет большое значение при закладке выработанных пространств, при погрузке добытой породы, при образований отвалов пустой порйдЫ и складов добытого полезного ископаемого и т. п. Разрыхляемость породы зависит от ее строения и сложения, твердости и способа добычи. Наиболее разрыхляемыми являются твердые и прочные породы. Наименьшей разрыхляемостью обладают малосвязные, рыхлые породы. Разрыхляемость данной породы может быть оценена коэфнцием- том 1-У AV ' v ~ V ' где - увеличение данного объема породы вследствие разрыхления и V— объем породы в массиве. Добытая порода состоит из кусков и частиц различных форм и размеров. Скопление таких кусков и частиц обладает большей пористостью я', чем пористость этой породы в массиве tt0. Это увеличение пористости и определяет разрыхляемость. С течением времени происходит усадка добытой породы — явление, обязанное действию силы тяжести, в результате которого куски и частицы располагаются в скоплении более плотным образом. При этом происходит уменьшение пористости, а вместе с тем и уменьшение коэфициента разрыхляемости. К такому же эффекту приводит и искусственное уплотнение добытой породы, например, трамбованием, не сопровождающимся разрушением кусков. Однако при всем этом объем добытой породы никогда не достигнет первоначального своего объема в массиве. Исключение составляют: песок и вообще грунты, искусственным уплотнением которых можно в отдельных случаях достигнуть большей плотности, чем плотность их в естественном состоянии. Усадке кускового материала способствует прибавление небольшого количества воды. Последняя, смачивая куски породы, играет роль смазки, уменьшающей трение между кусками и тем способствующей занятию отдельными кусками более устойчивого положения в скоплений, что и приводит к уменьшению объема, к усадке. Наибольшее числовое значение коэфициента разрыхления £ получается для свежедобытой породы, а наименьшее — для уплотненной породы, например, горным давлением (сухая закладка), при долгом лежании на складе и т. п. Разрыхляемость при наименьшем значении коэфициента ? называются остаточной. Если обозначить пористость при остаточной разрыхляемости череа п и составить выражение то это последнее может служить для бценки относительной уплот- няемости добытой породы. Это отношение вообще меньше единицы, и чем ближе оно к ней, тем большей уплотняемостью обладает данная добытая порода. Относительная уплотняемость имеет значение, например, при выборе состава сухой закладки выработанного пространства. Чем большей относительной уплотняемостью обладает данный закладочный материал, тем менее он пригоден для применения. Уплотняемость определенным образом связана с давлением. Допустим, что порода в кусках подвергается давлению без бокового расширения. Обозначим через /г0 высоту столба породы при начальном давлении р0 и через — при давлении рх. Площадь поперечного столба примем равной единице. Так как объем твердой части (скелета) столба остается все время без изменения, то Ml — %>= М1 — «|)> где я0 и пх— соответствующие значения пористости. Отсюда имеем: h0 _ 1 — пх hi 1 — щ и I щ ho — hi _ ftp — Л; Л0 в 1 — «1 — величину относительной усадки породы. Разность (й0 — Аг) представляет абсолютную величину усадки при увеличении давления от Ро ДО Pi- Опыты показывают, что кривые зависимости усадки рыхлого материала от давления, или так называемые компрессионные кривые, принадлежат к логарифмикам и имеют общее выражение г=-А1п(р4-Ре) + Сг, (а) где А,ре и Сг — постоянные величины для данной кривой, вычисляемые на основании определяемых опытом значений величины i для трех значений р. Явление усадки рыхлого материала под влиянием давления и без бокового расширения типично для закладки выработанного пространства. Заметим, что в этом случае с помощью формулы (а) может быть вычислена величина давления горных пород на закладку, вызвавшего наблюдаемую величину усадки I. Относительное увеличение объема породы при разрыхлении, оцениваемое коэфи- циентом может служить для приближенного определения высоты, на которую распространяется обрушение боковых пород в горизонтальных или наклонных выработках. При этом коэфнциент 5 определяется с помощью измерений осадки дневной поверхности (если, конечно, такая осадка наблюдается) и представляет собою некоторое среднее значение относительного увеличения объема в стесненных условиях для всей толщи пород между дайной выработкой и дневной поверхностью. Если величина деформации крепи потолка данной горизонтальной выработки — а и соответствующая осадка дневной поверхности—5 (по окончании процесса оседания), то при глубине заложения выработки Н получим, считая величину а весьма малой по сравнению с Н: В практике разработки каменноугольных месторождений коэфнциент $ обычно принимается равным (по Леонтовскому) для пород: слабых — 0,02J, средних — 0,025 и прочных — 0,030. Если высота горизонтальной выработки вчерне Л, то высота зоны обрушения определяется для случая незакрепленной выработки равной «о=Л для случая закрепленной выработки — Н(, == а : 5, где а—величина деформации крепи. В табл. 7 даны числовые значения коэфициента I для иекоторых пород для случая нестесненного увеличения объема. § 18. Сыпучие породы Сыпучая порода — скопление минеральных частиц (зерен, обломков) с незначительным сцеплением или вовсе лишенных сцепления между собою и весьма малых по сравнению с размерами всего скопления.
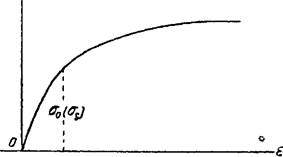
Свою форму сыпучая порода сохраняет вследствие веса частиц и трения между ними, называемого внутренним трением. Если боковая поверхность сыпучего тела плоская, то она имеет наклон к горизонту под некоторым углом а, не превышающим значения критического угла а0 для данного состояния сыпучего тела. То же относится и к наклону образующей при конической форме сыпучего тела. Угол а0 называется углом естественного откоса. С числовым значением этого угла связано условие предельного равновесия частиц на поверхности тела. Если вес какой-либо частицы на поверхности тела—q, то для момента предельного ее равновесия необходимо, чтобы тангенциальная составляющая веса ^sina0 была равна силе трения f-q-cosa0, и таким образом условием предельного равновесия является /=tga0, где /—коэфициент трения скольжения, который часто отождествляют с коэфициентом внутреннего трения tg<? и приходят к формальному выводу о равенстве для момента предельного равновесия угла естественного откоса а0углу внутреннего трения <р [16]. Между тем это не совсем согласуется с действительностью. Наблюдения показывают, что угол естественного откоса для дан»" ного состояния сыпучего тела является постоянной величиною, в то время как угол внутреннего трения является переменным, зависящим от нормального давления, в особенности при малых давлениях. Для песка, например, при давлении, меньшем 1 кг\смг, угол внутреннего трения уменьшается с увеличением давления и лишь при давлениях свыше 1 кг1см2 этот угол практически может считаться постоянным [17]. Угол или коэфициент внутреннего трения — величина, тесно связанная с сопротивлением сыпучего тела сдвигу. В этом отношении имеются многочисленные опытные данные [18]. Объяснением служит теория равновесия грунтов Кулона (1736—1806). Она может рассматриваться как частный случай теории прочности Мора. Скольжение (сдвиг) некоторой части сыпучего тела происходит при критическом напряжении т, которое связано с нормальным напряжением — т=/(о). При равновесии должно соблюдаться условие т<;/(о) для всевозможных положений площадки сдвига. По Кулону, . , .. 1ЙЧ *о +7°, (U8) где т0 — прочность на сдвиг, зависящая от сцепления, и /о — прочность, зависящая от трения с коэфициентом /. Если сцепление отсутствует, то Т-в/о, т. е. сопротявленйе сыпучего сДййгу является сОпрдтимеавем трению, прям® пропорциональным нормальному давлению. Опыт показывает, что выражение (1,18) до известной степени соблюдается лишь при давлениях, больших некоторой величины в*.' При меньших давлениях зависимость между х и о получается по закону кривой линии. На фиг. 10 показана диаграмма сдвига для связного трунта. Тангенс угла наклона кривой сдвига к оси давлений выража т собою коэфициент внутреннего трения. Для криволинейного участка диаграммы этот коэфициент представляет переменную величину. Угол внутреннего трения зависит также от содержания во^ ды в сыпучем теле. Влажный w-arctaf (В°ДЫ меньше 10% по весу) -.U-.-. . песок, например, имеет угол внутреннего трения больший-, чем в сухом песке. Однако для мокрого (10 — 25% воды по весу) песка этот угол уже меньше, чем для сухого. Во влажном и сыром песке с помощью воды создаются силы прилипания (молекулярного притяжения соприкасающихся поверхностей) и, таким об^а* зом, сопротивление сдвигу Фиг. 10. Диаграмма сдвига для связного грунта, увеличивается. В мокром же песке образуются водные пленки, которые играют роль смазки, уменьшающей сопротивление сдвигу. На величину угла внутреннего трения оказывает влияние тгкже и гранулометрический состав сыпучей породы: преобладание более крупных фракций увеличивает числовое значение этого угла.
В табл. 8 даны значения угла внутреннего трения' для некоторых пород.
§ 19. Плывучесть горных пород
Плывучими называются породы, обладающие в естественном состоянии свойством плывучести при их обнажении сбоку, например, при проведении вертикальной выработки. Этим свойством обладают при насыщении водою: мелкий песок с частицами 0,20 — 0,01 мм и мень В состоянии плывучести горная порода может быть рассматриваема состоящей из двух фаз- твердой и жидкой К твердой фазе относятся минеральные частицы крупностью свыше 0,005 мм, не способные длительное время находиться во взвешенном состоянии в жидкоя фазе и вообще быстро осаждающиеся. Жидкую фазу составляет вода со взвешенными в ней мельчайшими (меньше 0,005 мм) минеральными частицами, не способными осаждаться. Эти частицы участвуют в броуновском движении Считается, что каждая минеральная частица покрыта оболочкой связанной (адсорбированной) воды Эта последняя по тироде своей может быть гигроскопической водою, подчиняющейся законам адсорбции, или пленочной влагой Лебедева, или же водою сольватных обо лочек [19] Связанная вода обладает ссобыми физико-механическими свойствами по сравнению с водою гравитационной Эти свойства определяются лавным образом весьма большими мо текулярными давлениями (тысячи и десятки тысяч килограммов на кв. сантиметр), которые существуют в связанной воде Плотность этой воды больше единицы По Раковскому [20], например, плотность связанной воды на поверхности порошка крахмала составляет 1,28 — 2,45 г/см"*. Оболочки связанной воды вокруг частиц твердой фазы, повиди- мому, не играют большой роли. Что же касается оболочек этой воды вокруг минеральных частиц жидкой фазы, то они увеличивают плотность этой фпы Эта плотность может доходить до 1,5 и больше. Поэтому взвешивающее действие жидкой фазы оказывается большим, чем такое же действие чистой воды. Это действие уменьшает статическое трение между частицами твердой фазы, и устойчивость всей системы в целом оказывается более низкой, чем в случае, когда система состоит из одних частиц твердой фазы и чистои воды. В статическом состоянии системы жидкая фаза оказывает на твердую фазу всестороннее равномерное давление. При наличии небольшого напора возникает течение жидкой фазы, которая передвигается по порам между частицами твердой фазы. При этом последняя подвергается динамическому давлению. При известной величине напора в результате взвешивающего действия жидкои фазы и динамического давления нарушается устойчивость всей системы и возникает общее течение Чем больше в единице объема крупных, а следовательно, и более тяжелых частиц твердой фазы, тем меньше взвешивающий эффект жидкой фазы, и тем большее значение приобретает трение между этими частицами, и, таким образом, тем большей оказывается устойчивость системы При вполне \стоичивом состоянии твердой фазы явление сводится к обычной фильтрации. Крупнозернистые пески, например, с небольшой примесью илистых частиц и при небольших напорах не обладают плывучестью. Однако при больших на норах, а следовательно, при большом динамическом давлении, та кие пески могут оказаться плывучими.
Рассмотрим плывучую породу в простейших условиях, поместив ее на горизонтальн} ю плоскость с небольшой шероховатостью Течение этой породы здесь будет выражаться тем, что угол от- ^ ИМ Цимбаре ui Условием равновесия объема плывуна V будет: T + P = F или 7 sin a-j-Д tg a = 7/ cos a. (а) Так как угол а достаточно мал, то градиент tg а можно заменить через sin а, и тогда выражение (а) представится в виде: (7 -f- Д) sin a = 7/cos a, откуда Из (б) следует, что течение всей массы плывуна может иметь место в двух случаях: при /=0 или при 7 = 0. Первый случтй возможен, когда твердая фаза полностью находится во взвешенном состоянии, а второй — когда твердая фаза в составе плывуна отсутствует и когда, таким образом, последний представляет собою суспензию. Остановимся на первом случае. Если для некоторого объема плывуна обозначить через qc вес твердой фазы, то полное взвешивание этой фазы очевидно будет при условии qc = bf или I. е. когда удельный вес жидкой фазы будет равен объемному вес\ твердой фазы. Во втором случае суспензия может быть вполне уподоблена вязкой жидкости и к ней можно применить уравнение. Ньютона: do где т—касательное напряжение (внутреннее трение), действующее в плоскостях сдвигающихся слоев жидкости; v — скорость относительного сдвижения слоев; z — координата в направлении, перпендикулярном к направлению движения. Множитель -ц — коэфициент вязкости или просто вязкость. Этот коэфициент представляет собою константу, характеризующую жидкость. Впрочем, опыты с глиняными суспензиями показывают, что вязкость т) зависит от скорости [21J. Это явление носит название аномалии вязкости. Величина, обратная вязкости, представляет текучесть жидкости (точнее — коэфициент текучести). Обозначая ее через X, из уравнения Ньютона имеем- 1 dv_ т dz jnyrr —- Текучесть можно рассматривать как скорость одного (из двух горизонтальных) слоя жидкости по отношению к другому слою, если на единицу площади первого слоя действует тангенциальное усилие, равное единице, расстояние между слоями равно единице и пространство между слоями заполнено данной жидкостью. Текучесть характеризует подвижность жидкости. Возвращаясь к (б), отметим, что наибольшее значение tga будет при Д ~ 0, т. е. при отсутствии жидкой фазы. В этом случае масса породы будет сыпучим телом с характерным для него углом естественного откоса а. Условие (б) характеризует предельное статическое состояние плывучей породы. В состоянии текучести для нее будет иметь место условие- tg*> -LK- (в) 1 ч_ т По мере вытекания жидкой фазы будет увеличиваться коэфициент трения /, а вместе с тем и правая часть неравенства (в), что в конце концов и приведет к условию (б). Изложенное, конечно, далеко не исчерпывает проблемы плывунов. Основной остается задача динамикиj плывунов в условиях естественного залегания и при пересечении их выработкой. Эта задача еще не решена. § 20. Тепловые свойства горных пород Изменения температуры меняют состояние гооной породы, а следовательно, и все ее физико механические характеристики. Существенное значение имеют резкие колебания температуры, приводящие с течением времени породу к разрушению С углублением подземных разработок температура горных пород повышает ся в соответствии с геотермическим градиентом и, например, на глубине около 1 ООО м составляет 30—ЗУ. Проветривание подземных выработок способствует интенсивному теплообмену между обнажениями боковых пород и воздухом, понижает температуру этих пород в некоторой области, окружающей выработки. Обратное явление наблюдается в выработках, проведенных в полосе вечной мерзлоты. Здесь проветривание, в особенности в лешее время, повышает температуру боковых пород, вызывая оттаивание их. При искусственном замораживании горных пород, применяемом при проведении стволов шахт в особо тяжелых естественных условиях, температура пород понижается до —15° и больше, а затем, после проведения выработки, при искусственном оттаивании повышается до и больше. Тепловые свойства горных пород изучены слабо. Исключение составляют мерзлые грунты, механика которых трудами наших ученых (М. И. Сумгин, Н. А. Цы- тович и др.) в последнее время оформилась в стройную отрасль прикладных знаний. Тепловые свойства горных пород, как и других тел, ^характеризуются: теплопроводностью, теплоемкостью и объемным или линейным расширением. Теплопроводность горной породы в целом зависит от теплопроводности ее составных частей. Кристаллы имеют различную теплопроводность по различным направлениям. В этом отношении наблюдается большое сходство оптических и тепловых свойств кристалла. Оптически положительные кристаллы, за небольшими исключениями, термически также положительны. Теплота распространяется в них в направлении главной оптической оси с большей скоростью, чем в перпендикулярном направлении (в кварце, например, в 1,32 раза). Если в горной породе взять какое-либо направление то, следуя ему, получим на пути большое числое переходов от одних различно ориентированных минеральных зерен к другим, от зерен к пустотам (порлм) с водою или без нее и т. д. Эги переходы или контакты вызывают скачки температуры, усложняющие явление теплопровод locrn. При передаче теплоты от зерна с одной теплопроводностью к зерну с другой теплопроводностью имеет значение так называемая внешняя теплопроводность, зависящая от состава обоих зерен и вида контакта между ними Коэфициент внешней теплопроводности представляет количество тепла, которое 1еряется единицей поверхности контакта меладу зернами в единицу времени при разнице температур соприкасающихся зерен 1°. Сопротивл-ние пои прохождении теплоты через сложную породу равно сумме всех сопротивлений.
■щщшття По 1еплопроводности на первом Mecte стоя! щелочные Хлориды. Относительно высокой теплопроводностью обладают также сульфиды н окислы тяже- 1Ы\ металлов, Теплопроводность окислов примерно в сто раз меньше теплопроводности соответствующих металлов [22]. Лабораторные определения коэфициента теплопроводности показывают, что в (.реднем изверженные и метаморфические породы проводят тепло в 3—5 раз лучше, чем осадочные. Железистые кварциты, особенно же пирротин, имеют теплопроводность, близкую к теплопроводности металлов. Кроме минерального состава, на теплопроводность горной породы оказывают вчияние пористость (плотность) и влажность. Влияние пористости (плотности) усматривается из данных табл. 9 [5], а влияние влажности — из табл. 10.
Чем более сухой является порода, тем меньше ее теплопроводность. Песок с влажностью в 11,3% (по объему) имеет теплопроводность 0,0027, а совершенно сухой — только 0,0008. Установлено, что теплота лучше всего распространяется по плоскостям спайное! и. В сланцевых породах теплопроводность в направлении слоистости значи- 1ельно больше, чем в перпендикулярном направлении (для слюдяного сланца в трн раза). В табл. 11 даны значения коэфнцнента теплопроводности для некоторых горных пород. Таблица 11
3 Ь Теплоемкость (средняя) — отношение количества теплоты Q, сообщенной те- л\ в каком-либо процессе, к соответствующему повышению температуры Таким образом, '' р = 7^77 = ' dt> t, где си — истинная теплоемкость тела, определяемая при условии, что повышение температуры исчезающе мало. Теплоемкость зависит от температуры. При низких температурах она вообще ниже, чем при высоких. Исключение составляют барит и церуссит. Силикаты Са, Mg, Fe и А1 в интервале температур от 0 до 1 200° имеют теплоемкость примерно на 45% выше, чем в интервале от 0 до 100°. Если не считать чистых металлов, то наименьшей теплоемкостью обладают сернистые соединения. В табл. 12 даны значения теплоемкости для некоторых горных пород.
Кристаллы при нагревании расширяются различно по различным направлениям. В общем случае в кристалле различаются три термические оси. Это — направления наибольшего, среднего и наименьшего расширения. Эти оси в нагретом кристалле определяют эллипсоид. В кристаллах кубической сингонии тепловой эллипсоид обращается в шар. В тетрагональных и гексагональных кристаллах одна из осей теплового эллипсоида совпадает с главной оптической осью. В ромбических кристаллах оси эллипсоида параллельны кристаллографическим осям. В чоиоклннной сингонии одна из осей эллипсоида перпендикулярна плоскости симметрии и. наконец, в триклинных кристаллах тепловые оси вообще не совпадают с кристаллографическими. В зависимости от коэфициента расширения тепловой эллипсоид может быть вытянутым (известковый шпат) или же сплюснутым (кварц, гематит) по главной оси. У некоторых минералов (известковый шпат) при нагревании по некоторым направлениям получаются сокращения. В других минералах (кварц) расширение от нагревания в одном направлении превышает примерно в два раза расширения в других направлениях. Коэфициент линейного теплового расширения зависит от температуры. Для определенных температурных интервалов обычно пользуются средними значениями этого коэфициента. Значения его для некогорыл пород даны в табл. Ы.
Минералы и горные породы Каменная соль ........................... Песчаник (параллельно слоистости) Гранит (параллельно слоистости) Известняк ...................................
При нагреве кристалла в его слоях устанавливаются различные температуры i меньшающиеся по мере удаления от поверхности. Например, разница темпе- ратур между поверхностью кристалла, натретой солнцем до СО*, и слоем, расяо- ложениым на 1 см ниже, составляет около_5°. Эти различия температур создают неодинаковые расширения слоев. При нагревании связного кристаллического агрегата тепловое расширение вызывает механическое (растяжение, сжатие, сдвиг) взаимодействие между составными частями агрегата. В результате возникают внутренние напряжения, под влиянием которых появляются трещины, отслаивания и т. п. Эффект разрушения породы при этом во многом зависит от взаимного расположения зерен породы и состава их, определяющего величины теплового расширения и разные значения теплоемкости. Прн отрицательней температуре замерзает вода, находящаяся в порах и трещинах связной горной породы. При этом в первую очередь замерзает гравитационная вода, заключенная в наиболее крупных порах и трещинах. Что же касается воды, заключенной в тонких капиллярах, и вообще веды гигроскопической, удерживаемой молекулярным притяжением, то она может не замерзать при температурах —30° и ниже, оставаясь в переохлажденном состоянии. Переход воды в лед зависит, как известно, от температуры и давления. На диаграмме состояния тройная точка, отвечающая состоянию во ы в твердом, жидком и газо бразном состояниях, соответствует 0,0074° и давлению 4,583 мм рт. ст При переходе воды в лед имеет место увеличение объема приблизительно на 9%. Если вода заи ччняет не больше 85 90% объема пор. то это увеличение объема не оказывает влияния на прочность породы. Мерзлая горная порода представляет собою ноликристаллический агрегат, в кото; ом одним нз компонентом является лед. В связи с этим изменяются механические свойства породы. Ген юпроводность льда в несколько раз больше теплопроводности воды (соответственно 2,0 п 0 5 клл/м'час °С). В связи с этим теплопроводность мерзлой породы вообще больше теплопроводности этой же породы в обычных условиях. В мерзлой горной породе лед играет роль цемента. Поэтому прочность этой породы представляется повышенной. Упругие и пластические свойства горных пород с замерзшей в них водою, насколько известно, не изучены. Напротив, для льда и мерзлых i рунтов эти свойства исследованы довольно подробно. Об эте м см. специальные сочинения [*<3]. При исследовании механических свойств естественных грунтов существенное значение приобретает теория равновесного состояния воды в этих грунтах [Н]. Согласно этой теории, в любом мерзлом грунте прн любой его отрицательной температуре в природных условиях всегда содержится некоторое, хотя бы и весьма незначительное количество воды в жидкой фазе, находящееся в равновесном состоянии с величиной внешних воздействий и количественно изменяющееся с изменениями последних. ГЛАВА IV ДЕФОРМАЦИИ ГОРНЫХ ПОРОД § 21. Предварительные замечания В этой главе рассматриваются более подробно вопросы, затронутые в предыдущей главе и относящиеся к упругой и пластической деформациям горных пород. При этом обращается, наибольшее внимание на самый механизм деформации — вопрос, имеющий существенное значение для оценки деформаций обнажений пород при горных разработках. Данная глава имеет два раздела. В первом из .них освещаются результаты, добытые при экспериментальном исследовании образцов горных пород. Во втором же разделе приводятся иллюстрации основных выводов первого раздела в условиях литосферы. Деформация юрной породы во многом определяется деформацией составляющих ее кристаллов. Поэтому изучение следует начать с последних. В этом отношении имеются достаточно подробные экспериментальные данные для минеральных и металлических кристаллов и, в частности, особенно подробные данные для каменной соли. Однако, в отличие от металлических, минеральные поликристаллы (горные породы) изучены совсем недостаточно. Многочисленные испытания образцов j-орных пород, выполненные разными исследователями во второй половине прошлого и в начале текущего века, имели в виду главным образом потребности стропильного дела. Испытания были ограничены получением лишь некоторых средних механических характеристик, относящихся к агрегату в целом при простых напряженных состояниях. Более подробный материал был получен при исследованиях в последнее время Были установлены существенные закономерности и дано теоретическое объяснение отдельным фазам деформации горных пород в массиве и вообще в условиях сложного напряженного состояния. Получил развитие структурный анализ горных пород — весьма эффективное средство исследования [25]. А. ОПЫТНЫЕ ИССЛЕДОВАНИЯ КРИСТАЛЛОВ И ОБРАЗЦОВ ГОРНЫХ ПОРОД § 22. Деформация кристаллов Исследования показывают, что [кристаллы способны деформироваться не только упруго, но и пластически. Последнее для них яв ляется одним из типичных свойств. В начале наблюдается упругая деформация. В упругой области по снятии нагрузки главная часть напряжений исчезает быстро — со скоростью звука в данной среде, другая же, небольшая, часть напряжений исчезает медленно. Нагревание ускоряет процесс восстановления формы кристалла, а охлаждение замедляет его. Сдвиги, наблюдаемые при повышении напряжений за предел упругости, могут быть в виде трансляции или двойникования. Трансляция происходит в определенных кристаллографических плоскостях и направлениях, например в кристаллах каменной соли — по плоскости (100) в направлении [110]. В результате сдвига на боковой поверхности кристалла появляется ряд узких полосок. Считают, что плоскости скольжения — плоскости с наиболее густым расположением атомов, направление же скольжения отвечает наиболее тесному расположению атомов [26]. В процессе деформации кристалла растяжением слои между плоскостями скольжения монотонно изгибаются. В результате одна часть каждого слоя оказывается растянутой, а другая часть сжатой. Чем больше степень деформации, тем больше изогнутость плоскостей скольжения. При исследовании деформации с помощью рентгеновых лучей на рентгенограмме отмечается вытягивание приблизительно круглых пятен в хвосты (явление астеризма). Это отвечает возникновению периодического изгиба слоев, в который переходит изгиб монотонный [27]. Этот переход сопровождается образованием в поверхностях скольжения весьма малых кристаллических осколков. Изгиб слоев и эти осколки затрудняют скольжение. Возрастает сопротивление сдвигу и для продолжения процесса деформации требуется увеличение касательного напряжения или, другими словами, растягивающей нагрузки. Следствием этого является более быстрый рост напряжений, чем возрастание деформации. Это и есть явление упрочнения кристалла в процессе пластической деформации. Не входя в рассмотрение природы упрочнения, которая далеко еще не выяснена, отметим, что степень упрочнения кристалла зависит от температуры и скорости деформации. При повышении температуры сопротивление сдвигу умёньшает- ся. Поэтому, например, если при некоторых нагрузке и температуре пластическая деформация еще не начинается, то при той же нагрузке и при ьслее высокой температуре она может начаться. При высоких температурах небольшой рост напряжений сопровождается значительной и длительной деформацией, переходящей в течение. При низких температурах, наоборот, наблюдается более быстрый рост напряжений.
©2015-2020 studopedya.ru Все права принадлежат авторам размещенных материалов.
|
 i}
i}