Направление и распределение горного давления

Вопросы, сюда относящиеся, несмотря на то, что они весьма часто ставятся практикой,изучены весьма слабо.

Возьмем горизонтальную выработку. Если все условия симметричны 01носительно вертикальной оси этой выработки, то горнбе давление со стороны потолка, боковое и со стороны почвы будет также рас-

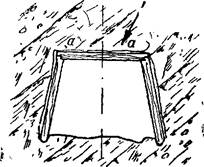
125

пр^делейо симметрично. При этом-направление давлений со стороны потолка и почвы будет вертикальным, а боковое — горизонтальным.

Однако если симметрия условий отсутствует, то во многих слу­чаях наблюдается неравномерность распределения давления и откло­нение его направления от нормального, свойственного симметричным условиям. В этом отношении можно привести следующие типичные примеры.

Горизонтальная выработка проводится по простиранию слоистых пород наклонного или крутого падения, имеющих слабые контакты

по поверхностям наслоения (фиг. 68). Здесь обычно наблюдается косона- правленное горное давление, обязан­ное сдвигам по слабым контактам между породами. Этому в особенности способствует наличие естественных трещин, расположенных под прямым или близким к нему углом к поверх­ностям напластования. Трещины вы­деляют участки породы а, слабо свя­занные с окружающей массой и при известных условиях способные сколь­зить книзу. Теоретически такое сколь­жение возможно при условии а><р, если а — угол падения пород и <р—угол трения скольжения породы по породе.

Так как обычно угол ср превышает 20 — 25°, то косонаправленное горное давление и наблюдается при наклонном или крутом падении слоев При этом чем больше угол падения, тем все более интенсив-

Фиг. 69. Неравномерный прогиб кровли в штреке с раскоскою.

ным наблюдается косонаправленное давление Это и понятно, сдви­гающие усилия возрастают пропорционально синусу угла падения слоев. Направление и распределение косонаправленного давления должны быть изучены в каждом отдельном случае. Отметим здесь также, что при наклонном или крутом залегании слоев широкие горизонтальные выработки (камеры) целесообразно располагать вкрест простирания пород, а не по простиранию, когда действию косо- направленного горного давления подвергается длинная сторона выра­ботки.

Асимметричное горное давление типично также в штреках по простиранию тонких угольных пластов, проведенных с раскоскою, в особенности односторонней (фиг. 69). Вследствие различной жест­кости угля, крепи штрека и сухой закладки имеет место неравномер-

«я

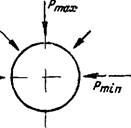
- % ' ^ Г

ный прогиб кровли. Зта^неравномерабсТь еще ооЛее усиливаемся лри наклонном залегании угольного аласта. В особенности же отчетливой она оказывается вообще на участках штреков, находящихся в об- тсти влияния очистных работ Здесь прибретает значение опорное давление, вызываемое опусканием кровли над выработанным прост­ранством (при работах с закладкою) или же образованием некоторого свода (при работах с обрушением). Давление это, распределенное по некоторому закону, имеет наибольшую величину вблизи очистной вы­работки и затем, вниз по падению, посте­пенно уменьшается

Косонаправленное и при том неравномер­ное горное давление, обязанное наклонному или крутому залеганию слоев со слабыми контактами, имеет место и при проведении вертикальных стволов шахт (фиг 70) Здесь со стороны восстания обычно отмечается наи­большее давление, а со стороны простира­ния—наименьшее Чем больше угол падения слоев, тем больше неравномерность давле­ния

§ 69 О теориях горного давления

Выше было отмечено, что учение о гор"

ном давлении находится еще на опытном ну"

ти Этот этап проходит в своем развртии

каждая естественная наука Ему свойственны

гипотезы, выдвигаемые для объяснения тех

или иных явлений или данлых эксперимента

В частности, такие гипотезы предложены и

в отношении горного давления Эти гипоте-

зы, называемые теориями, весьма многочис- 'Щпп

леины Почти каждый исследователь вносил

в учение о горном давлении что-либо новое

и создавал свою оригинальную теорию ,

Приступая к краткому обзору некоторых Фиг. 70. Неравномерное гор-

из этих теорий, заметим прежде всего, что все ^ное давление в вертикальном

^r ' г — стволе шахты

они имеют в виду величину установившегося

I орного давления при симметричных естественных условиях. Почти все теории рассматривают явление без учета влияния рудничной кре­пи Поэтому, если иметь в виду определение горного давления, данное в § 63, то все эти теории по существу не могут быть строго названы теориями горного давления Они скорее относятся к проблеме устойчивости обнажений горных пород в выработках или, точнее, к состоянию обнажений после потери устойчивости Наибольшее число ^еорий имеет в виду свод ^брхшенда__а„горизонтальной выработке Тфи симметричных*условиях Величина механических усилий, кото­рые развиваются при обрушении, и принимается в качестве величи­на горного давления, независимо от того, какая крепь будет постав­лена Горное давление при расчете крепи рассматривается как по­верхностная сила Таким образом, нй одна из характеристик, о которых шла речь в $ 66, предложенными теориями не освещается, если не считать величины установившегося горного давления. Это составляет общую черту теорий Большинство из них относится к горизонтальным выработкам, в частности к горному давлению со сто­роны кровли

А. Теории горногодкбЯйнйя в Горизонтальный

ВЫРАБОТКАХ

Вводные замечания

В § 64 были рассмотрены последовательные фазы процесса потеря устойчивости обнажением. Здесь мы покажем, что многие теории, трактующие о горном давлении в горизонтальной выработке, отно­сятся к отдельным фазам указанного процесса. Большинство из них имеет в виду свод обрушения

Прогиб кровли

Прогиб непосредственной кровли не является, конечно, самосто­ятельным про1ибом только одного ее-нижнего слоя или пласта. Про­гибаются также и вышерасположенные породы. При этом стрела прогиба отдельных пластов постепенно уменьшается в направления кверху

Фиг. 71. Волна давления

-t=

Прогиб пласта непосредственной кровли был рассмотрен Шульцем еще в 1867 г [76]. Автор ограничился упругим прогибом, уподобив пласт балке, равномерйонагруженной и заделанной по концам, и цди-_ менив простейшие расчетные приемы- сопротивления материалов. При этом он вычислил предельную величину пролета, при котором пласт еще не обрушается под влиянием собственного веса.

Нужно заметить, что применение формул сопротивления материалов к расчетам, подобным указанному, вообще никогда не дает резуль­татов, подтверждаемых опытом. Это объясняется неоднородностью горных пород и, в частности, например, как в задаче Шульца, рас­смотрением слоя породы изолированно от окружающих пород, что в действительности не имеет мёста. (Зднако качественная сторона явления во многих случаях удовлетворительно объясняется с по­мощью аналогий, заимствованных из теории сопротивления материа­лов.

С прогибом непосредственной кровли < в очистной выработке полЬгапщюющегр угольного пласта связана так назШаШЗя теория ..волрц давления" [77]. "Под влийШ т "Собственно г jo весГ й "некоторой части веса вышележащих пород в рабочем пространстве очистной выработки прогибается пласт непосредственной кревлй

Этот пласт представляется бад!со^'аадеяанной~4№огр^ниденно своим к о нпрмЗ а^забо ем Б^ -твко^- вадедюа. u-apoti

забоя лояеляются моменты •^эшнеки^шзьшшощие волнообразный'йз-» г^пласта(фигГП^Какуказывают,явление ошбен5о~отчетлибо наблю­дается в случае достаточно жесткого пдаСтанепосредственной кровли (например, песчаника), заключенного между пластичными угольный пластом и вышележащей породой. Вследствие, сопротивления пород

Волнообразный изгиб сравнительно быстро затухает впереди забоя. Утонение угольного пласта наблюдается на расстоянии длины полу­волны от забоя, и это место отвечает наибольшему горному давлению. Различают волны стоячие (когда забой не движется) и движущиеся.

Фиг. 72. Пластический прогиб кровли.

По некоторым данным длина стоячей волны в условиях Рейнско- Вестфальского округа составляет около 40 м, а длина движущейся волны в тех же условиях — около 15 м. Воспользовавшись уравне­нием изгиба балки на упругом основании, В. Д^Сле^щм^эазвил тео­рию волны давления более подробно [69].

Волна давления относится к области явлений упругости. Этим, повидимому, и объясняются известные трудности непосредственного ее наблюдения. Однако в отличие от упругого, пластический прогиб пород во многих случаях отчетливо лаблюдается на практике. Впрочем подробные исследования его, если не считать имеющихся весьма тща­тельных маркшейдерских измерений так называемых движений боко­вых пород, отсутствуют.

При изгибе кровли вблизи опор обычно имеет место растяже­ние, а посередине пролета — сжатие (фиг. 72), что является следствием совместного действия веса вышележащих пород и.бокового давле­ния. Пластический прогиб кровли связан с временем и, в частности, со скоростью подвигания забоя. В связи с этим важное практическое значение имеет интенсивность опускания кровли, в особенности в очистных выработках (лавах). В этом отношении подробные измере­ния опускания кровли при разработке пологопадающих угольных плас­тов в Донецком бассейне были выполнены В. Т. ДавчлИНДЁИ.!⁷^ Подоб­ные же исследования выполнялись и другими авторами (С. Г. Аирртцррим., Г. Н. К^знец2|ы*м|1 др.)

§ 72. Образование трещин

Эта фаза потери прочности обнажением изучалась преимущест­венно в кровле очистных выработок в связи с вопросами управления кровлей. В этом отношении в специальной литературе имеются мно­гие данные.

Считают, например, что трещины отвечают вообще плоскостям на­слоения или связывают образование трещин с давлением в пяте свода естественного равновесия пород [44]. Одни авторы указывают, что решающее значение для образования трещин имеют напряжения сдвига [79], другие отмечают постоянство в углах падения (50 — 60°) трещин, появляющихся в кровле. В. Д. Слесарев, сопоставляя мно­гочисленные данные наблюдений и опыт, приходит к заключению „о полной идентичности происхождения трещин в кровле с трещинами- сдвигами, появляющимися в" образцах твердых тел при их испытании на раздавливание" [69].

Подобных мнений можно было бы провести много и все они лиш­ний раз свидетельствовали бы о большом разнообразии отдельных соображений и взглядов по вопросу о непосредственных причинах и закономерностях образования трещин. Это вполне понятно: естест-

9 П №. Цимв«ревич

венные условия, в которых имели место,наблюдения отдельных иссле­дователей, были самыми разнообразными.

Если порода кровяи однородна в отношении состава и строения, то во многих случаях характер трещин и места их появления вполне

отвечают таковым при де­формации отдельно взя­той балки. В частности это имеет место в лавах Подмосковного бассейна, где залегает в кровле пласт темной глины. Так называемые „обрезы кров­ли" у забоя, наблюдаемые здесь'и служащие причи-

Фиг. 73 Непосредственная кровля при работах НОЮ ее обрушения, ПреД- с обрушением ставляют следы трещин

разрыва Эти последние появляются у забоя вверху пласта при его изгибе как консоли (фиг 73).

На фиг. 74 дан фотоснимок модели штрека в плотной глине, подверженного давлению сверху и с боков. В стенках выработки от­четливо наблюдаются трещины скольжения.

Фиг 74 Деформация стенок штрека (фото).

§ 73. Свод обрушения '

Процесс трещинообразования, когда число ^рещин в кровле все более увеличивается с увеличением их размеров и проникновением в глубь массива, многими исследователями рассматривается как про­цесс сводообразования.

Большинство предложенных теорий имеет в виду сформировав­шийся в потолке выработки свод обрушения. Вес породы внутри
этого свода, полный или неполный, и принимается за величину да§- ления горной породы на крепь, препятствующую выпадению этой породы. Существенно заметить, что ни одна из теорий не останав­ливается на вопросе, почему именно при обрушении потолка выра­ботки получается свод естественного равновесия. Всюду просто

обрушения.

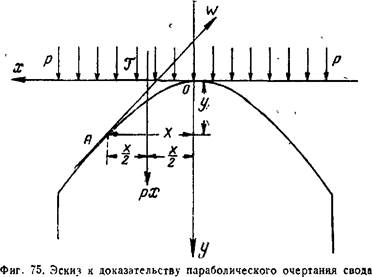
принимается на основании данных наблюдений, что при обрушении получается свод.

Теоретически доказывается, что свод обрушения имеет очертание по параболе. Действительно, если рассматривать условия равновесия элемента свода АО (фиг. 75), симметрично и равномерно нагружен­ного сверху весом вышележащих пород, то равенство нулю <^уммы моментов сил (относительно точки А), действующих на выделенный элемент, дает

Ту = О,

где р — вертикальная нагрузка на единицу горизонтальной проекции свода и Г—горизонтальный распор свода. Откуда

У = -& (1,73)

— уравнение параболы в прямоугольных координатах с началом в вершине кривой.

Параболическое очертание свода обрушения — общая черта пред­ложенных теорий. Различия относятся к размерам свода или, точнее, к высоте свода, так как пролет свода, равный ширине выработки, является всегда известным. Разными теориями высота свода обруше­ния определяется по-разному. Ни одна из теорий не учитывает на­личия крепи. Просто предполагается, что крепь имеется и на нее оказывает давление вес породы, заключенной внутри свода. При этом, в зависимости от тех или иных соображений, вес этот принимается полным или же уменьшенным.

М. М. Протодьяконов определяет размеры свода обрушения сле­дующим образом [76]' В потолке горизонтальной выработки шири­ною 2а залегает сыпучая порода объемного веса f и с коэфициентом
внутреннего трения /. Равновесие образовабЩег'ося сйода обрушейий высотою b возможно и будет наиболее устойчивым, когда частицы породы прижаты друг к другу и какие бы то ни было сдвигающие усилия отсутствуют. На свод действует равномерно распределенная нагрузка 2Р = 2ра (фиг. 76).

В точке опоры А равнодействующая R нагрузки на левую поло­вину свода имеет составляющие: горизонтальную Т и вертикальную Р.

Для того, чтобы частица А не сдвинулась и, таким образом, не было бы нарушено равновесие свода, нужно соблюдение условия

Т</ра

или, лучше, условия

Г+ к = fpa,

где к — некоторый запас, в наибольшей степени обеспечивающий устойчивость свода. Этот запас автор предстёйляйт В ййдё горизон­тальных сдвигающих усилий т (считая т на единицу вертикальной проекции свода Ь). Таким образом:

T-{-xb=fpa. (а)

Уравнение направляющей кривой свода (1,73) для точки А дает:

Р^аг и

Подставляя сюда из (а) значение Т и решая относительно т, по­лучим:

2 fb — a

55Г— .

Отсюда можно определить высоту свода b из условия, /чтобы за­пас х был наибольшим. После простейших действий это условие полу­чается следующим:

и ^а

ь=_т,

и уравнение кривой свода принимает вид:

Для того чтобы перейти от сыпучей породы к связной, достаточ­но в (2,73) заменить коэфициент трения коэфициентом крепости [76].

Таким образом, размеры параболического свода известны: пролет его— 2а и высота — Ь. Величина горного давления на крепь равна весу породы в объеме этого свода и на единицу длины выработки составляет-

Q = f-f- ⁽⁴'⁷³⁾

Изложенная теория была проверена автором ее на опыте (ящик с песком, имеющий вырез в днище). Она является одной из самых по­пулярных, чему способствует чрезвычайная простота окончательных формул. Между тем, она включает в себе некоторые спорные поло­жения. В этом отношении она была подробно рассмотрена В. Д. Сле- саревым [69].

Рассмотрим вкратце еще некоторые теории.

В основе теории, предложенной Риттером [76], лежит предполо­жение, что на крепь воздействует избыток веса породы, заключенной внутри свода параболической формы, над сопротивлением отрыву этой породы от поверхности свода. После вычислений автор получает окончательную формулу давления горной породы на крепь на единицу длины горизонтальной выработки в следующем виде:

где k = c (сила сцепления) :f (объемный вес). Эта теория не получила практического применения. Подробно ее рассматривал М. М. Прото­дьяконов [76].

В тоннельном деле в свое время имела применение теория, на основании которой высота свода обрушения определяется по прогибу кровли выработки [76]. Этот прогиб является следствием увеличе­ния объема породы, разрыхленной внутри свода. Если наблюденный прогиб кровли посередине пролета выработки е и относительное ли­нейное увеличение данной породы при раздроблении трещинами п, то высота свода обрушения будет

Величина п определяется в лаборатории.

Принимая далее для простоты, что свод обрушения имеет очер­тание по эллипсу с полуосями а и Ь, давление на крепь на единицу длины выработки получается равным

Q—■ (6.73)

Нетрудно видеть, что данная теория включает ряд условностей. В горном деле она не получила применения.

В. Д. (^есапев предложил теорию горного давления, во многом отличную от предыдущих [69]. Он различает следующие три зоны, окружающие горизонтальную выработку: зону, непосредственно при­легающую к выработке н называемую им зоной Тромпетера, зону повышенных напряжений и зону напряженного состояния нетронутого массива. Зона Тромпетера характеризуется отсутствием напряжений и отделяется от соседней зоны повышенных напряжений замкнутой кривой давления. Эта последняя представляет собою, по автору, рав­нодействующую пучка силовых линий, обтекающих выработку прн создании новых условий равновесия под действием следующих сил: веса-столба породы до поверхности, бокового- давления и давлений со стороны почвы выработки. В зависимости ot условий кривая дав­ления может относиться к мгновенному равновесию действующих сил (неустойчивое равновесие) или же отражать устойчивое равнове­сие. В последнем случае она должна удовлетворять требованиям, предъявляемым к кривым давления в теории сводов. Эта кривая в потолке выработки представляется параболой, отграничивающей зону Тромпетера и при устойчивом равновесии определяющей свод обру­шения. Вес породы внутри этого свода и представляет величину гор­ного давления. Наибольший подъем этой кривой в потолке равен

(7,73)

Atg(-f-T-)'

где а —- полупролет выработки; h — глубина расположения выработки, считая от дневной поверхности до пят свода; ср — угол трения породы (характеристика связной породы, предложенная автором теории).

Условие устойчивости свода обрушения выражается так:

где угол а определяется из:

------- fT _Л ■ (8.73)

Величина давления на крепь, считая на единицу длины выработки, равна

Q = 4-W, (9,73)

где подъем свода у определяется из (7,73).

В данной теории искусственным является представление о зоне, называемой зоной Тромпетера, которая в реальных условиях не на­блюдается, а также представление о пучке силовых линий.

Ограничимся изложенными теориями, заметив, что прибавление к ним существующий других теорий, также основанных на принципе свода обрушения, не внесло бы большей ясности в рассматриваемую проблему.

Поиск по сайту: