 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Критерій найбільшого припустимого відхилення. Загальний підхід.
Выбор шага дискретизации с использованием данного критерия производится в предположении, что исходное сообщение восстанавливается с помощью полинома степени n. На некотором отрезке времени [t0, tn] для равноотстоящих отсчетов восстановленное сообщение х'(t) может быть представлено выражением:
Вводя сокращенную запись, получим:
Для восстановления функции х(t) c помощью полинома степени n необходимо иметь n+ 1 отсчетов. Погрешность восстановления исходного сообщения в этом случае определится остаточным членом:
где
где ε0 — допустимая погрешность дискретизации по времени, можно найти шаг дискретизации или длину интервала tn — t0, на котором-нужно определить п + 1 отсчетных значений непрерывного сообщения. При этом интервал tn — t0 является некоторой функцией погрешности ε0, степени воспроизводящего полинома и т. д. Интерес представляет определение шага дискретизации при использовании воспроизводящих полиномов нулевой и первой степени. Нулевой степени воспроизводящего полинома соответствует ступенчатая аппроксимация непрерывного сообщения. В этом случае (1-90) примет вид: откуда При n = 1 (линейная аппроксимация) остаточный член определится
Максимизируя произведение
Пропускна спроможність дискретного каналу без завад. Под дискретным каналом передачи информации принято понимать совокупность средств, предназначенных для передачи дискретных сигналов. Пропускная способность дискретного канала без помех, в котором используется m символов с длительностью Общее количество сообщений L, имеющих длительность
Найдем значение пропускной способности:
Когда
Поиск по сайту: |



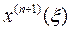 — значение (n + 1)-й производной сообщения х (t) взятой в некоторой точке ξ, лежащей внутри интервала tn — t0. Поскольку положение точки ξ неизвестно, для оценки используют модуль максимального значения производной Мn+1 на заданном интервале. Тогда
— значение (n + 1)-й производной сообщения х (t) взятой в некоторой точке ξ, лежащей внутри интервала tn — t0. Поскольку положение точки ξ неизвестно, для оценки используют модуль максимального значения производной Мn+1 на заданном интервале. Тогда Введя ограничение
Введя ограничение 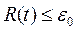



 получим
получим  откуда
откуда 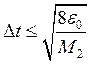
 . Символы считаются независимыми и любая последовательность символов представляет некоторое сообщение. Взяв в качестве исходного выражение
. Символы считаются независимыми и любая последовательность символов представляет некоторое сообщение. Взяв в качестве исходного выражение  , определим количество информации в сообщении и найдем пропускную способность.
, определим количество информации в сообщении и найдем пропускную способность. , определяется как сумма количеств сообщений, оканчивающихся символами
, определяется как сумма количеств сообщений, оканчивающихся символами 
 ,
, 

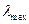 - корень характеристического уравнения
- корень характеристического уравнения , то
, то 