 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Оптимальное кодирование. Критерий оптимальности кода
Оптимальное статистическое кодирование обеспечивает минимизацию среднего количества кодовых символов на один элемент сообщения. Этим обеспечивается получение максимально возможного количества информации, передаваемого кодовыми комбинациями при заданной длительности работы канала, а следовательно, и пропускной способности канала. Все они должны обеспечивать решение' двух основных задач: 1)при заданной статистике источника сообщений формирование кодовых комбинаций со статистическими характеристиками, при которых достигается приближение скорости передачи информации к пропускной способности канала; 2)возможность однозначного декодирования сигналов на приемной стороне.( ни одна из кодовых комбинаций не является началом другой. Этим обеспечивается требование разделимости кодовых комбинаций, т. е. возможность однозначного декодирования сигналов.) Критерий оптимальности кода. Оптимальное согласование сообщения с каналом будет при выборе длительностей символов сообщения в соответствии с выражением
или в другой записи для случая, когда
Из (II1-60) следует, что длительности символов сообщения должны быть пропорциональны логарифму вероятности их появления, т. е. наиболее вероятные символы должны иметь наименьшую длительность, а наименее вероятные — большую длительность. Если символы данного сообщения не удовлетворяют условиям оптимального согласования, они могут быть при согласовании заменены другими символами в соответствии с условиями (111-60) или (111-61). Такая замена называется оптимальным кодированием. Оптимальные коды: код Шеннона- Фано и код Хаффмена.
Код Шеннона-Фано. При отсутствии статистических связей между символами скорость передачи информации будет максимальна при условии равной вероятности передачи символов 0 и 1. В соответствии с этим построение кода Шеннона-Фано производится методом дихотомий (последовательного деления пополам). Все подлежащие кодированию символы сообщения разбиваются на две группы так, чтобы суммы вероятностей появления элементов сообщений в каждой группе были бы по возможности одинаковы. В результате такого разбиения как бы образовано новое сообщение, состоящее всего из двух элементов вероятности появления которых примерно одинаковы. Всем символам первой группы приписывается 0 и всем символам второй группы – 1. Каждая из полученных групп затем разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс деления повторяется до тех пор, пока в каждой подгруппе останется по одному символу. --------- Правило построения кода заключается в следующем: 1.Символы исходного сообщения (буквы) располагаются в порядке убывания их вероятности и разбиваются на две группы так, чтобы суммы вероятностей в группах были примерно одинаковы. 2.В качестве первого символа кода всем буквам, вошедшим в первую группу, приписывается единица, а буквам второй группы —нуль. 3.Каждая из полученных групп вновь разбивается на две подгруппы примерно с одинаковыми вероятностями. 4.Буквам первых подгрупп в качестве следующего символа кода приписывается единица, а к буквам второй подгруппы —нуль и т. д. Разбиение на подгруппы производится до тех пор, пока в каждой .подгруппе не останется по одной букве. ---------
Поиск по сайту: |
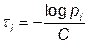 (II1-60}
(II1-60}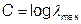
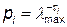 (111-61)
(111-61)