 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие информации. Измерение информации.
Информация – это сведенья, которые можно хранить, передавать и преобразовывать. Это снятие неопределенности о каком-нибудь объекте. Сообщение – это форма представления информации, удобная для передачи по линии связи. Существует три основных направления при измерении информации: · Структурное: учитывает дискретное строение информации. Подсчет информации осуществляется простым подсчетом информационных элементов комбинаторным методом: · Статистическое: учитывает вероятность появления сообщений. Все значения измеряемой величины рассматриваются, как исходы опыта. Сумма вероятностей всех исходов · Семантическое: учитывает целесообразность, полезность и смысловую наполненность информации.
Спектр ССП Стационарный в узком смысле, если его функция распределения плотности вероятности произвольного порядка n не меняется при любом сдвиге всей группы точек t1 , t2 … tn вдоль оси времени. То есть pn(x1,t1; x2,t2; ...; xn,tn) = pn(x1, t1 + τ; x2, t2 + τ; ...; xn,tn + τ). Вероятностные характеристики СВП в узком смысле не меняются в случае изменения расположения отсчетной точки на временной оси. Стационарным в широком смысле называют процесс, математическое ожидание которого не зависит от времени, а корреляционная функция зависит только от разницы t2 – t1 = τ и не зависит от самых интервалов t1 и t2. Энергетический спектр стационарного процесса может быть определен двумя путями: - непосредственным наблюдением одной реализации - нахождением преобразования Фурье от корреляционной функции. Использование преобразования Фурье к случайным процессам невозможно по таким причинам: 1) Реализации случайного процесса 2) Для случайного процесса Можно обобщить гармонический анализ, усредняя спектральные разложения, полученные для отдельных реализаций:
Учитывая, что
Поиск по сайту: |
 , где L – количество возможных сообщений, n – количество элементов сообщения, m – алфавит. Если имеем k источников сообщений, то количество возможных сообщений от всех источников
, где L – количество возможных сообщений, n – количество элементов сообщения, m – алфавит. Если имеем k источников сообщений, то количество возможных сообщений от всех источников  . Чтобы сохранялось свойство аддитивности, используют логарифмическую меру Хартли
. Чтобы сохранялось свойство аддитивности, используют логарифмическую меру Хартли  . Если имеем несколько источников, то количество информации от всех источников
. Если имеем несколько источников, то количество информации от всех источников 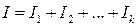 .
. . Формула Шеннона используется для измерения информации при этом подходе:
. Формула Шеннона используется для измерения информации при этом подходе:  , где
, где 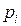 - вероятность появления i-го символа.
- вероятность появления i-го символа.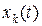 и нахождением предела;
и нахождением предела; не удовлетворяют условию абсолютной интегрируемости
не удовлетворяют условию абсолютной интегрируемости  .
. частотный спектр также является случайной функцией.
частотный спектр также является случайной функцией.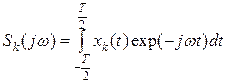 . Средняя мощность сигнала:
. Средняя мощность сигнала:  . Также средняя мощность выражается через частотный спектр:
. Также средняя мощность выражается через частотный спектр:  . Функция под интегралом называется спектральной плотностью мощности
. Функция под интегралом называется спектральной плотностью мощности  . Найдем спектральную плотность совокупности реализаций (путем усреднения по ансамблю).
. Найдем спектральную плотность совокупности реализаций (путем усреднения по ансамблю).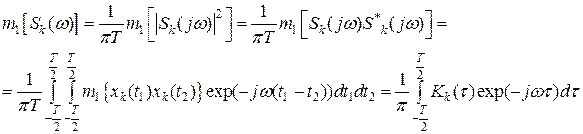
 , имеем преобразования Винера-Хинчина:
, имеем преобразования Винера-Хинчина: ,
, 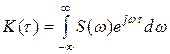 . Спектральная плотность является прямым преобразованием Фурье от корреляционной функции.
. Спектральная плотность является прямым преобразованием Фурье от корреляционной функции.