 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Семантичний підхід до визначення кількості інформації
Семантические меры информации оценивают смысл, содержание информации, ее целесообразность и существенность. Содержательность события Оценка содержательности базируется на математической логике, в которой логические функции истинности Логическая оценка количества информации имеет внешнее сходство со статистической.
Отличие логической оценки в том, что она учитывает меры истинности или ложности событий, а не вероятности их реализаций. Существенность информации отражает степень важности информации о том или ином значении параметра Полезность информации для решения данной задачи можно оценивать по эффекту, который оказывает полученная информация на решение задачи. Если вероятность достижения цели увеличивается, тo информацию следует считать полезной. Можно также оценивать полезность информации числом попыток, которые совершает получатель информации для достижения цели. При таких оценках информация может быть пустой, если она не изменяет вероятности или числа проб для достижения цели, положительной или отрицательной величиной. Можно также оценивать ценность сообщений с помощью теории статистических решений. В этом случае во внимание принимается цель, с которой передается сообщение, т. е. учитываются результаты использования сообщений. Для оценки вводятся две характеристики: ценностная энтропия и ценность информации. Под ценностной энтропией, понимают средние потери при определённой выбранной стратегии.
22.3 Построение циклического кода Сущеествует два способа построения циклического кода: 1) Комбинации циклического кода можно построить путем умножения исходной кодовой комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю два. - если старшая степень произведения меньше (n-1), то получим полином представляет кодовую комбинацию циклического кода. - если старшая степень произведения больше (n-1), то полином делится на заранее выбранный полином степени n, и результатом умножения считается полученный остаток от деления. При таком способе образования циклического кода, информационные и контрольные символы не отделены друг от друга, что затрудняет процесс дэкодирования. 2) Комбинация А(х) умножается на xk при этом длина кодовой комбинации возрастает на к разрядов. А(х) xk делим на образующий полином G (х) , в результате деления получаем остаток R (х) При таком построение циклического кода контрольные символы находятся в конце. При использовании циклического кода для исправления ошибок места искаженных символов определяются путем анализа остатка, получающегося при делении принятой комбинации на образующий полином.
Поиск по сайту: |
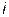 выражается через функцию меры
выражается через функцию меры  – содержательности его отрицания
– содержательности его отрицания  , где
, где  – содержательность события
– содержательность события 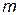 – функция меры,
– функция меры,  – знак отрицания.
– знак отрицания. имеют формальное сходство с вероятностью события и его отрицания:
имеют формальное сходство с вероятностью события и его отрицания: 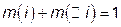 и
и 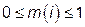 .
. где
где  – логическая оценка количества информации.
– логическая оценка количества информации. с учетом времени
с учетом времени  и пространства
и пространства  .
.