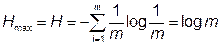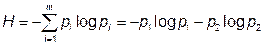|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Правила построения кода Хеминга⇐ ПредыдущаяСтр 11 из 11
Предназначенный для обнаружения и исправления однократной ошибки. При построении кода каждый из k проверочных символов определяется как результат суммирования по модулю 2 определенного сочетания информационных символов. В результате этого сумма проверяемых информационных и контрольного символа всегда является четной. Количество контрольных символов определяется по формуле: В коде Хэмминга проверки на четность организованы таким образом, что получается число, указывающее номер позиции, на которой произошло искажение. При проверке на четность мы используем номер позиции соответствующие единице находящейся в том разряде, какую проверку мы делаем, то есть если 1проверка, то смотрим единицы по первому разряду, и т.д. например:
Если число единиц на проверочных позициях четное то контрольный символ равен 0, а если число единиц на проверочных позиция не четное, то контрольный символ равен 1. После окончания проверки мы узнаем, на какой позиции находится ошибочный символ, если таковой имеется, по результату проверок, поскольку оно организовано таким образом , что получается число указывающее на номер позиции на которой произошло искажение.
Код Хаффмена Хаффманом предложена методика, позволяющая построить оптимальный код с минимальной избыточностью при любом основании кода m. Правило построения кода заключается в следующем: 1.Символы сообщений (буквы) располагаются в порядке убывания вероятностей. 2. 3.В качестве последних символов кода, приписываемых буквам, вошедшим во вспомогательную букву, выбирается 4.Оставшиеся буквы и вспомогательная буква располагаются в порядке убывания вероятностей. 5. Составляется вторая вспомогательная буква, в которую входят m наименее вероятных букв. Вошедшим буквам присваиваются различные символы кода и т. д. Властивості ентропії Энтропия – это количество информации приходящейся на один символ сообщения. Энтропия характеризует источник сообщений с заданным алфавитом и является мерой неопределенности, которая имеется в ансамбле сообщений этого источника. Чем больше энтропия, тем больше информации несет в себе сообщение источника, тем большая неопределенность снимается при получении сообщения. Обычно энтропия обозначается буквой Н и определяется выражением:
Дискретным называется сигнал состоящий из отдельных элементов (букв, символов, импульсов ) принимающих конечное число различных значений. Свойства энтропии : 1. Энтропия - функция распределения вероятностей. 4. Энтропия является величиной вещественной ограниченной и неотрицательной, т. е. H>0. Это свойство следует из выражения (I—14) с учетом того, что величины рi являются неотрицательными величинами и заключены в промежутке 0 <= рi <= 1. 5. Энтропия минимальна и равна нулю, если сообщение известно заранее, т. е. если рi= 1, а р1 = р2 = ... = рi-1 =рi+1 = ...=рn.=0. 6. Энтропия максимальна, если все состояния элементов сообщений равновероятны. Данное свойство энтропии легко доказывается с помощью методов вариационного исчисления. Мы воспользуемся конечным результатом, согласно которому Н = Нтах, если
4.Энтропия бинарных сообщений может изменяться от нуля до единицы. Бинарные сообщения характеризуются использованием двоичного алфавита, т. е. т = 2. Для таких сообщений
Поиск по сайту: |
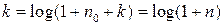 ,де
,де 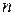 -количество символов в кодовой комбинации. Контрольные символы располагаются на местах определенных по степеням двойки (1, 2, 4, 8, 16…)
-количество символов в кодовой комбинации. Контрольные символы располагаются на местах определенных по степеням двойки (1, 2, 4, 8, 16…)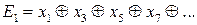
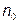 наименее вероятных букв объединяются в одну вспомогательную, вероятность которой определяется суммой вероятностей входящих в нее букв. Число
наименее вероятных букв объединяются в одну вспомогательную, вероятность которой определяется суммой вероятностей входящих в нее букв. Число  , так чтобы выполнялось соотношение
, так чтобы выполнялось соотношение 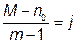 , где М – число символов сообщения; j – целое число.
, где М – число символов сообщения; j – целое число.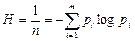 .
.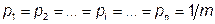 ,
,